تحلیل واریانس یک طرفه با مثال در SPSS

برای توضیح آنالیز واریانس یک طرفه ابتدا بهتر است با یک مثال کاربردی آغاز کنیم.فرض کنید می‌خواهیم میانگین دو جامعه را مقایسه کنیم. مثلاً اگر بخواهیم در یک سازمان بررسی کنیم آیا میانگین حقوق کارمندان زن با میانگین حقوق کارمندان مرد متفاوت است، از آزمون تی استفاده می‌کنیم. اما اگر میانگین بیش از دو جامعه را بخواهیم مقایسه کنیم چطور؟

مثلاً فرض کنید در همان سازمان مذکور، بخواهیم میانگین حقوق کارمندان با سطح تحصیلات مختلف (شامل دیپلم، کارشناسی، کارشناسی ارشد و دکترا) را مقایسه کنیم.در این صورت می‌توانیم از آنالیز واریانس استفاده کنیم. در ادامه به تحلیل واریانس یک‌طرفه در SPSS و همچنین یک مثال کاربردی می پردازیم.آنالیز واریانس ابزاری آماری است که برای بررسی برابری میانگین‌های دو یا تعداد بیشتری از گروه‌ها استفاده می‌شود تا مشخص شود آیا به طور معنی‌دار با هم متفاوت هستند یا خیر. آنالیز واریانس، اثر یک یا تعداد بیشتری عامل را با مقایسه میانگین‌های نمونه‌های متفاوت، بررسی می‌کند. 

آنالیز واریانس یک‌ طرفه چیست؟

آنالیز واریانس یک‌ طرفه (one-way ANOVA) میانگین‌های دو یا تعدادی بیشتر از گروه‌های مستقل در جامعه را مقایسه می‌کند و هدفش این است که مشخص کند آیا شواهد آماری وجود دارد که میانگین آن گروه‌ها به طور معنی‌دار متفاوت هستند یا خیر. آنالیز واریانس یک‌طرفه یک آزمون پارامتری است. این آزمون‌ با این نام‌ها نیز شناخته می‌شود: آنوای تک‌عاملی، آنوای یک‌طرفه و آنوای بین‌عاملی. متغیرهایی که در این آزمون استفاده می‌شوند عبارتند از: 1- متغیر وابسته. 2- متغیر مستقل (متغیر گروه‌بندی یا عامل نیز نامیده می‌شود). متغیر مستقل، اعضای جامعه را به چند گروه یا سطح مستقل تقسیم‌بندی می‌کند.نکته 1: تحلیل واریانس یک‌ طرفه و آزمون تی دو نمونه مستقل هر دو می‌توانند میانگین‌های دو گروه را مقایسه کنند. منتها آنالیز واریانس یک‌طرفه  قادر است میانگین‌های سه یا تعدادی بیشتری از گروه‌ها را نیز مقایسه کند.نکته 2: اگر متغیر گروه‌بندی (متغیر مستقل) تنها دو گروه داشته باشد، آن گاه نتایج تحلیل واریانس یک‌طرفه و آزمون تی دو نمونه مستقل یکسان خواهد بود. در حقیقت، اگر هر دوی این آزمون‌ها را استفاده کنیم خواهیم دید t2=F، که در آن t آماره آزمون تی دو نمونه مستقل و F آماره آزمون فیشر در تحلیل واریانس یک‌ طرفه است.

شرایط داده‌ها برای آنالیز واریانس یک‌ طرفه

داده‌های مورد استفاده در تحلیل واریانس یک‌طرفه باید شرایط (پذیره‌های) زیر را داشته باشند:

1. متغیر وابسته، پیوسته باشد (یعنی در مقیاس بازه‌ای یا نسبتی باشد)،
2. متغیر مستقل، دسته‌ای باشد (یعنی دارای دو یا بیشتر گروه باشد)،
3. هر سطر از داده‌ها دارای هر دو مقدار متغیر مستقل و متغیر وابسته باشد،
4. گروه‌ها مستقل باشند، هیچ رابطه‌ای بین آزمودنی‌ها (اعضا) در هر نمونه وجود نداشته باشد. این یعنی:

• آزمودنی‌های گروه اول نمی‌توانند در گروه دوم نیز باشند،
• هیچ آزمودنی در هیچ گروهی نمی‌تواند بر آزمودنی‌های گروه‌های دیگر اثر داشته باشد، 
• هیچ گروهی نمی‌تواند بر گروه دیگر اثر داشته باشد.

5. نمونه‌ای تصادفی از جامعه باشد.
6. توزیع (تقریباً) نرمال از متغیر وابسته داشته باشیم. در این ارتباط به نکات زیر باید توجه کنیم:

• توزیع غیرنرمال، مخصوصاً توزیع‌هایی که به طور جدی چولگی دارند، به مقدار زیادی توان آزمون را کاهش می‌دهند، در این حالت بهتر است شما ازآزمون کروسکال والیس (Kruskal–Wallis H test یاone-way ANOVA on ranks ) استفاده کنید.
• در نمونه‌های متوسط تا بزرگ، عدم نرمال بودن می‌تواند تا حدودی به p-مقدارهای تقریباً دقیق منجر شود.

7. همگنی واریانس‌ها وجود داشته باشد. یعنی واریانس در همه‌ی گروه‌ها تقریباً برابر باشد. در این مورد داریم:

• وقتی این پذیره نقض شود و حجم نمونه در گروه‌ها متفاوت باشد، آن گاه p-مقدار برای آزمون F کلی قابل اعتماد نیست. در این شرایط باید از آماره‌های جایگزینی استفاده کرد که شرط برابری واریانس در میان جوامع را در نظر نمی‌گیرند، از قبیل آماره براون-فورس (Browne-Forsythe) یا آماره وِلش (Welch) که در قسمت Options پنجره ANOVA در SPSS قرار دارند.
• وقتی این پذیره نقض می‌شود، حتی وقتی حجم نمونه گروه‌ها تقریباً برابر باشد، ممکن است نتایج آزمون‌های تعقیبی درست نباشد. وقتی واریانس‌ها نابرابر باشند، باید از آزمون‌های تعقیبی که به شرط برابری واریانس احتیاج ندارند استفاده کرد (مانند آزمون سیِ دانِت (Dunnet)).

8. هیچ داده‌ی پرتی نباید وجود داشته باشد.

نکته 3: وقتی شرایط نرمال بودن، همگنی واریانس و عدم وجود داده پرت برای آنالیز واریانس یک‌طرفه مهیا نباشد، می‌توان به جای آن از آزمون ناپارامتری کروسکال-والیس (Kruskal-Wallis) استفاده کرد.در استفاده از آنالیز واریانس یک‌طرفه معمولاً از قوانین سرانگشتی زیر استفاده می‌شود:

• در هر گروه باید حداقل 6 آزمودنی وجود داشته باشد (البته حجم نمونه‌ی بیشتر بهتر است).
• طرح‌ها تا حد امکان متوازن باشند. طرح متوازن طرحی است که حجم نمونه در گروه‌ها یکسان است. در طرح‌هایی که به طور شدید نامتوازن باشند امکان نقض پذیره‌هایی که ذکر شد زیاد است و منجر به عدم اعتبار نتایج آزمون F می‌شوند.

فرضیات

فرضیه صفر و فرضیه یک در آنالیز واریانس یک‌ طرفه به صورت زیر بیان می‌شود:(میانگین‌های هر k گروه برابر هستند)       

                                                                                      حداقل یکی از میانگین‌ها با بقیه متفاوت است.که در آن میانگین گروه i ام جامعه (i=1,2,…,k) است.نکته 4: آنالیز واریانس یک‌طرفه یک آزمون کلی‌نگر است زیرا آزمون F ، معنی‌داری کل مدل را به طور کلی نشان می‌دهد؛ یعنی نشان می‌دهد آیا هیچ تفاوت معنی‌داری در میانگین‌های بین هر کدام از گروه‌ها وجود دارد یا خیر. به عبارت دیگر این آزمون بیان می‌کند حداقل یکی از میانگین‌ها با بقیه متفاوت است. اما این آزمون تعیین نمی‌کند کدام یک از میانگین‌ها متفاوت است. برای تعیین این که دقیقاً کدام یک از جفت‌های میانگین‌ها به طور معنی‌دار متفاوت هستند به آزمون‌های تعقیبی نیاز است.

آماره آزمون

آماره آزمون برای تحلیل واریانس یک‌طرفه با F نشان داده می‌شود. برای یک متغیر مستقل با k گروه، آماره F بررسی می‌کند آیا میانگین‌های گروه‌ها به طور متفاوت معنی‌دار هستند. برای محاسبه‌ی جملاتی که در فرمول F هستند از جدول زیر استفاده می‌شود:که در آن:آماره F به صورت زیر محاسبه می‌شود: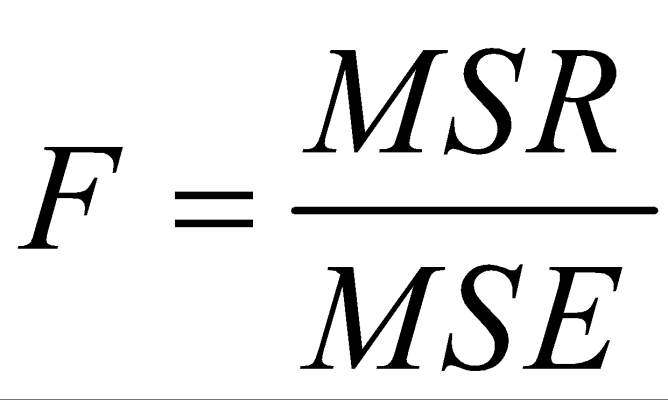در توضیحات بالا، تیمار (مدل) و خطا رایج‌ترین اصطلاحات مورد استفاده در متون علمی و متون سنتی طرح آزمایش‌ها هستند. در علوم اجتماعی، از اصطلاح بین‌گروهی برای تیمار و درون‌گروهی برای خطا استفاده می‌شود. در SPSS نیز از همین اصطلاحات استفاده می‌شود.

ایجاد فایل داده

در فایل داده‌ها باید حداقل دو متغیر وجود داشته باشد که در هر ستون نمایش داده می‌شوند. متغیر مستقل باید از نوع دسته‌ای یعنی اسمی (nominal) یا رتبه‌ای (ordinal) و شامل حداقل دو گروه باشد. متغیر وابسته نیز باید پیوسته (scale) باشد. هر سطر از داده‌ها باید اطلاعات مربوط به یک آزمودنی جداگانه را نشان دهد.یکی از آزمون ها و روش های پر کاربرد در مباحث آماری پایان نامه آنالیز واریانس است، شما می توانید از افراد متخصص در حوزه آماری برای انجام آنالیز واریانس یک طرفه استفاده کنید.

در ادامه سعی شده با مثالی کاربردی آموزش گام به گام تحلیل واریانس یک طرفه در SPSS برای شما تبیین گردد. اما این نرم افزار قابلیت های زیادی را در علم آمار دارد. چنانچه علاقه مند به این نرم افزار و مباحث آماری هستید می توانید از آموزش هایی همچون آموزش نرم افزار SPSS استفاده کنید.

نرم افزار SPSS چیست؟ کاربرد نرم افزار SPSS در آمار چیست؟

مثالی برای آزمون تحلیل واریانس یک‌طرفه(یک راهه) در SPSS

برای اجرای تحلیل واریانس یک‌ طرفه در SPSS از مسیر زیر اقدام می‌کنیم:

                                                                                                                               Analyze > Compare Means > One-Way ANOVA

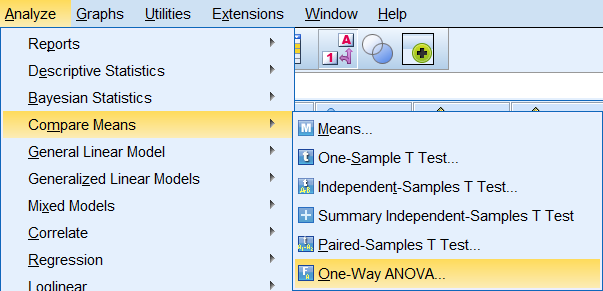سپس در پنجره‌ی ظاهر‌شده، باید متغیرهای حاضر در تحلیل را مشخص کنیم. این پنجره همانند شکل بعد است. در این پنجره همگی متغیرهای حاضر در فایل داده‌ها ظاهر می‌شوند که باید با استفاده از کلید‌های فلش آبی‌رنگ آن‌ها را به قسمت‌های مربوطه منتقل کنیم.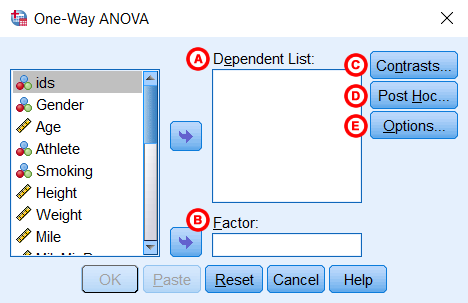در پنجره‌ی فوق، قسمت‌های مختلف بدین شرح است:A- فهرست متغیرهای وابسته: در این قسمت متغیر یا متغیرهایی وارد می‌شوند که قصد مقایسه‌ی میانگین‌های سطوح آن‌ها را داریم. اگر در این قسمت بیش از یک متغیر وارد کنیم، آن گاه نرم‌افزار به طور جداگانه برای هر کدام از آن‌ها آنالیز واریانس یک‌ طرفه انجام می‌دهد.B- عامل: متغیر مستقل است که قبلاً توضیحات آن ارائه شد. C- مقابله‌ها: استفاده از این گزینه اختیاری است و منجر به انجام مقایسه‌های برنامه‌ریزی شده بعد از اجرای آزمون آنالیز واریانس کلی می‌شود. پنجره مربوط به آن در شکل بعد آمده است: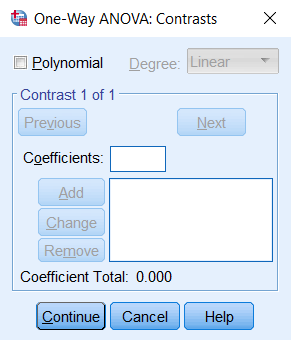وقتی آزمون F اولیه وجود تفاوت معنی‌دار بین میانگین گروه‌ها را نشان دهد، مقابله‌ها برای تعیین این که کدام یک از میانگین‌ها به طور معنی‌دار متفاوت هستند می‌تواند استفاده شود. البته از آن زمانی می‌توان استفاده کرد که فرضیه‌های مشخصی درباره‌ی میانگین‌ها برای آزمون کردن داشته باشیم. در حقیقت، مقابله‌ها پیش از آغاز آنالیز واریانس یک طرفه تعیین می‌شوند. مقابله‌ها واریانس را به مؤلفه‌های تشکیل‌دهنده‌ی آن تقسیم می‌کنند. از آن‌ها برای استفاده از مقایسه‌های نامتعامد، مقابله‌های استاندارد و مقابله‌های چندجمله‌ای (تحلیل روند) استفاده می‌شود.D- آزمون‌های تعقیبی: این آزمون‌ها با عنوان مقایسات چندگانه نیز شناخته می‌شوند و استفاده از گزینه مربوطه اختیاری است. پنجره مربوط به آن همانند شکل زیر است و در آن آزمون تعقیبی دلخواه را می‌توان فعال کرد: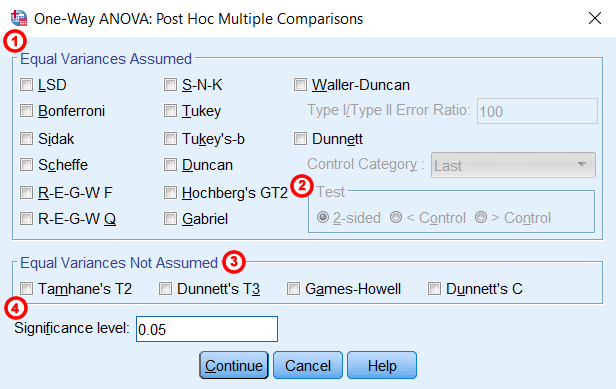در پنجره‌ی فوق، قسمت‌های مختلف بدین شرح است:

1. برابری واریانس: این قسمت مربوط به آزمون‌های تعقیبی است که به شرط همگنی واریانس نیاز دارد (همه گروه‌ها دارای واریانس یکسان هستند).
2. آزمون: در آزمون دانِت، به طور پیش‌فرض، یک فرضیه دوطرفه در آزمون‌های تعقیبی مورد آزمون قرار می‌گیرد. اما به جای آن می‌توان یک فرضیه یک‌طرفه را نیزآزمون کرد. ابتدا آزمون دانت را علامت بزنید و سپس تعیین کنید آیا دسته‌ی مربوط به گروه کنترل در اولین یا آخرین گروه متغیر مستقل مورد نظر ما است. در قسمت آزمون (Test)، روی <Control یا >Control کلیک کنید. در این فرضیات باید تعیین کنیم آیا ادعای ما بر اساس کوچک‌تر بودن میانگین گروه کنترل از گروه دیگر است (>Control) یا بر اساس بزرگ‌تر بودن میانگین گروه کنترل از گروه دیگر است (<Control).
3. عدم برابری واریانس: در این قسمت آزمون‌هایی قرار دارند که به شرط برابری واریانس گروه‌ها احتیاج ندارند. 
4. سطح معنی‌داری: مقدار مورد نظر برای سطح معنی‌داری را در این قسمت وارد می‌کنیم. مقدار آن به طور پیش فرض برابر با 05/0 است.

آزمون‌های تعقیبی را زمانی می‌توان استفاده کرد که آزمون F وجود تفاوت‌های معنی‌دار بین میانگین‌های گروه‌ها را نشان می‌دهد. این ازمون‌ها زمانی به کار می‌آیند که بخواهیم تعیین کنیم کدام میانگین‌ها به طور مشخص با بقیه به طور معنی‌دار متفاوت هستند و از قبل نیز هیچ فرضیه‌ای در مورد آن‌ها نداریم. آزمون‌های تعقیبی همانند آزمون t جفت‌های میانگین‌ها را مقایسه می‌کنند، اما برخلاف آزمون t ، این آزمون‌ها مقدار معنی‌داری را برای لحاظ در مقایسات چندگانه تصحیح می‌کنند.E- گزینه‌ها: با کلیک روی این گزینه، پنجره‌ای ظاهر می‌شود که در آن آماره‌هایی را که در خروجی ظاهر می‌شوند تعیین می‌کنیم. این گزینه‌ها عبارتند از: آماره‌های توصیفی، اثرات ثابت و تصادفی، آزمون همگنی واریانس، آزمون براون-فورس و آزمون ولش، رسم نمودار میانگین‌ها، و چگونگی برخورد با داده‌های گمشده. پنجره مربوطه همانند شکل زیر است: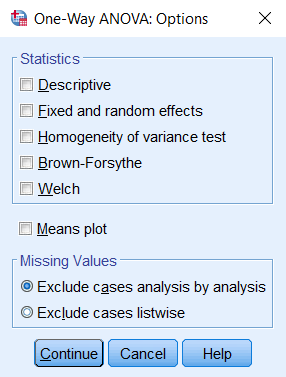پیاده سازی تحلیل واریانس یک طرفه در SPSS تا اینجا قدم به قدم بیان شد، حال در ادامه شما با یک مثال کاربردی روبرو می‌شوید، اما چنانچه شما به مباحث تحلیل آماری علاقه دارید می توانید مطالب بیشتری را در مرجع تحلیل و آموزش آماری ببینید.مثال آنالیز واریانس یک طرفهدراین جا از مثالی استفاده می‌کنیم که نتایج آن تقریباً واضح است و هدف، نشان دادن عملیات انجام‌شده در پس تحلیل واریانس یک‌ طرفه است.بیان مسئله: در فایل داده‌های این مثال، Sprint زمان انجام دوی سرعت (بر حسب ثانیه) در یک فاصله‌ی مشخص، و Smoking نشان‌دهنده‌ی وضعیت مصرف سیگار (صفر: غیرسیگاری، یک: قبلاً سیگاری و دو: در حال حاضر سیگاری) است. از آنوا برای آزمون وجود تفاوت معنی‌دار در زمان دوی سرعت بر حسب وضعیت مصرف سیگار استفاده می‌شود. متغیر وابسته به صورت زمان دوی سرعت و متغیر مستقل به صورت وضعیت مصرف سیگار است.پیش از انجام آزمون، نگاهی به آماره‌های توصیفی متغیرها می‌اندازیم. برای این کار از مسیر زیر استفاده می‌کنیم:

Analyze > Compare Means > Means

در این صورت خروجی زیر ظاهر می‌شود: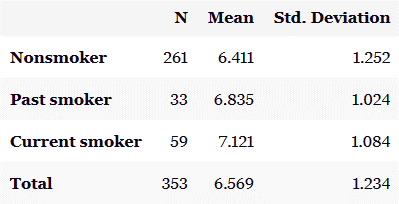در خروجی فوق، میانگین دوی سرعت 6.6 با انحراف معیار 1.2 است (با تعداد 353 آزمودنی معتبر). در این خروجی، هم چنین میانگین و انحراف معیار میانگین دوی سرعت در هر کدام از گروه‌های نوع مصرف سیگار مشاهده می‌شود. توجه کنید در این مثال تعداد کل آزمودنی‌ها 374 است که به دلیل وجود داده‌های گم‌شده در برخی گروه‌ها، در خروجی فوق تعداد کل آزمودنی‌ها 353 نمایش داده شده است. در نهایت می‌توان با استفاده از نمودار جعبه‌ای به ایده‌ای کلی از توزیع داده‌ها بر حسب گروه‌ها دست یافت: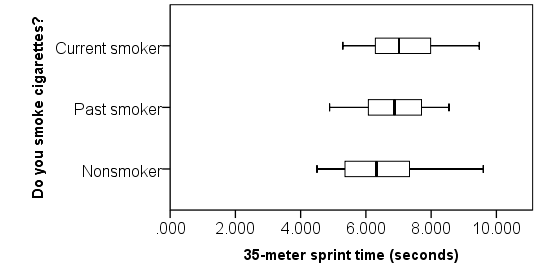بر اساس نمودار جعبه‌ای، می‌توان دید هیچ داده‌ی پرتی وجود ندارد، توزیع داده‌ها تقریباً متقارن است، و مرکز توزیع گروه‌ها چندان متفاوت با هم به نظر نمی‌آیند. اما میانه زمان دوی سرعت برای غیرسیگاری‌ها کمی سریع‌تر (بزرگ‌تر) از میانه‌ی آن برای گروه قبلاً سیگاری‌ها بوده است.اجرای روال: ابتدا از مسیری که پیشتر توضیح داده شد، پنجره‌ی آنالیز واریانس یک‌ طرفه را باز می‌کنیم. در قسمت متغیر وابسته Sprint و در قسمت فاکتور Smoking را وارد می‌کنیم. با کلیک روی Options، نمودار میانگین‌ها را انتخاب می‌کنیم و در نهایت OK را می‌زنیم.اولین خروجی ظاهر‌شده، جدول آنالیز واریانس است که به صورت شکل زیر است: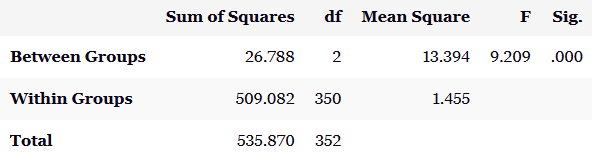در خروجی هم‌چنین نمودار میانگین‌ها نیز به نمایش درآمده است: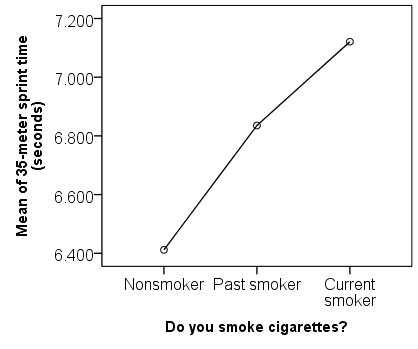نمودار میانگین‌ها نمایشی بصری از آن مواردی است که در جدول مقایسه میانگین‌ها دیدیم. نقاط روی این نمودار به صورت میانگین هر گروه است. در این نمودار مشاهده‌ آن که سیگاری‌های حال حاضر میانگین دوی سرعت کندتری دارند ساده‌تر است. هم چنین به سادگی نیز می‌توان دید که غیرسیگاری‌ها سریع‌ترین میانگین دوی سرعت را دارند.

تفسیر خروجی آنالیز واریانس یک طرفه

با توجه به نتایج جدول تحلیل واریانس یک طرفه ، نتیجه می‌گیریم که میانگین دوی سرعت در حداقل یکی از گروه‌های وضعیت مصرف سیگار متفاوت است (F2,350=9.209, p<0.001). توجه کنید که در این حالت آزمون تحلیل واریانس نمی‌گوید دقیقاَ کدام میانگین(ها) با بقیه متفاوت هستند. برای تشخیص آن، باید از آزمون‌های تعقیبی (مقایسات چندگانه) به شرحی که پیشتر گفته شد استفاده کرد.

کاربرد آنالیز واریانس یک طرفه در فصل چهارم پایان نامه

از رایج‌ترین کاربردهای آزمون آنالیز واریانس در فصل چهارم پایان نامه می‌توان به مقایسه میانگین چند جامعه مستقل نام برد. فرض کنید بخواهیم میزان رضایت شغلی را در بین افرادی که در سمت‌ها مختلف (مدیران ارشد، مدیران رده میانی و کارمندان) مشغول به کار هستند مقایسه کنیم و در این رابطه فرضیه تحقیق که “میزان رضایت شغلی در میان مدیران ارشد، مدیران رده میانی و کارمندان تفاوت معناداری دارد” را آزمون کنیم.H₀: میزان رضایت شغلی در میان مدیران ارشد، مدیران رده میانی و کارمندان تفاوت معناداری ندارد.H₁ (فرضیه تحقیق): میزان رضایت شغلی در میان مدیران ارشد، مدیران رده میانی و کارمندان تفاوت معناداری دارد.برای این کار میزان رضایت شغلی را با استفاده از پرسشنامه استاندارد مینه سوتا اندازه‌گیری می‌کنیم و در کنار ثبت پاسخ‌های افراد سمت کاری افراد را هم ثبت خواهیم کرد. این پرسشنامه دارای 19 سوال بوده و هدف آن بررسی ابعاد رضایت شغلی در 6 بعد نظام پرداخت (سوالات 1،2،3)، نوع شغل (سوالات4،5،6،7)، فرصت­های پیشرفت (سوالات8،9،10)، جوّ سازمانی (سوالات11،12)، سبک رهبری (سوالات13،14،15،16)، شرایط فیزیکی (سوالات17،18،19) می‌باشد و نمره کلی رضایت شغلی از جمع نمرات این 6 بعد به‌دست می‌آید.برای انجام آزمون آنالیز واریانس با استفاده از SPSS متغیر گروه (سمت کاری) به صورت 1: مدیران ارشد، 2: مدیران رده میانی و 3: کارمندان کدگذاری شده و در فیلد Factor وارد می‌شود. و در قسمت Dependent List متغیر رضایت شغلی را وارد می‌کنیم. 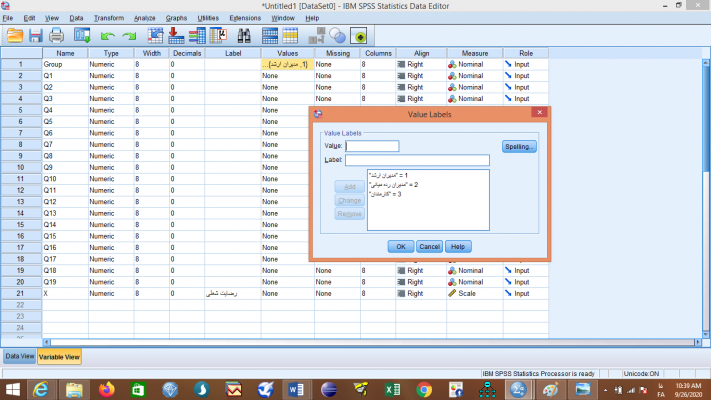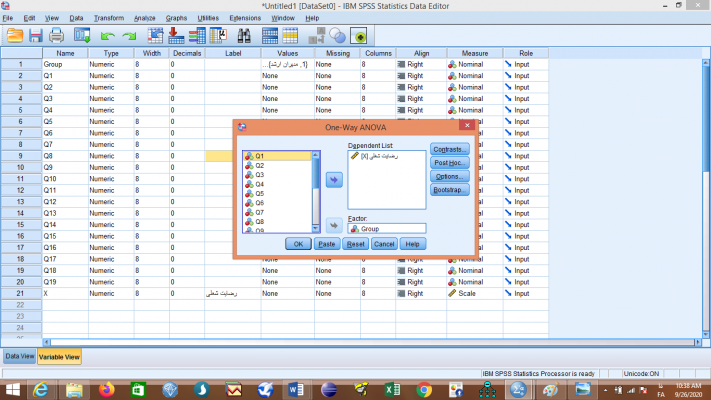چنانچه بخواهیم هر یک از ابعاد رضایت شغلی را به صورت جداگانه بررسی کنیم، این ابعاد را وارد Dependent List می‌کنیم.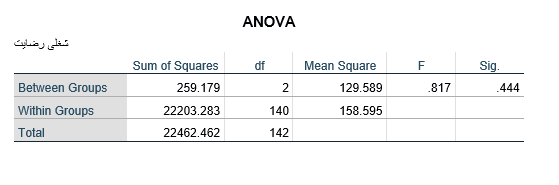مطابق نتایج به‌دست آمده مقدار معناداری آزمون آنالیز واریانس بزرگتر از 05/0 (444/0) به‌دست آمده است بنابراین نمی‌توان فرضیه H₀ را رد کرد و برای تایید فرضیه تحقیق با عنوان “میزان رضایت شغلی در میان مدیران ارشد، مدیران رده میانی و کارمندان تفاوت معناداری دارد.” نیاز به شواهد بیشتری داریم.در مثال دیگر فرض کنید بخواهیم اثر گوگرد در کاهش بیماری گال پوستی سیب زمینی را بررسی کنیم. علاوه بر کرت‌های بدون گوگرد که به عنوان شاهد در نظر گرفته شده‌اند، تاثیر 3 مقدار از گوگرد در بهار و 3 مقدار از آن در پاییز با مقادیر 336، 673 و 1345 کیلوگرم در هکتار مورد مقایسه بوده است. بدین ترتیب روی هم رفته 7 تیمار در آزمایش بکار رفته است. صفت مورد اندازه‌گیری درصد آلودگی در غده‌های سیب زمینی است.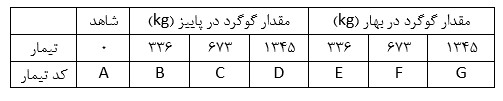H₀: گوگرد در کاهش بیماری گال پوستی سیب زمینی اثری ندارد.H₁ (فرضیه تحقیق): گوگرد در کاهش بیماری گال پوستی سیب زمینی اثر دارد.برای انجام آزمون آنالیز واریانس تیمار در فیلد Factor و درصد آلودگی در غده‌های سیب زمینی در قسمت Dependent List وارد می‌شود.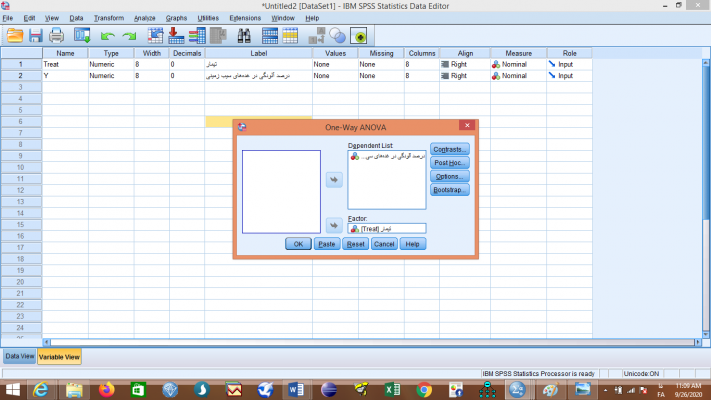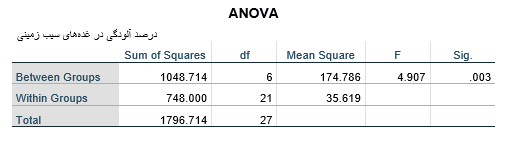مطابق نتایج به‌دست آمده مقدار معناداری آزمون آنالیز واریانس کوچکتر از 05/0 (003/0) به‌دست آمده است بنابراین فرضیه H₀ رد می‌شود و درصد آلودگی غده‌های سیب‌زمینی در تیمارهای متخلف از گوگرد تفاوت معناداری دارد و گوگرد در کاهش بیماری گال پوستی سیب زمینی اثر دارد.به خاطر داشته‌باشید در این مثال متغیر وابسته رضایت شغلی و متغیر مستقل سمت کاری افراد (مدیران ارشد، مدیران رده میانی و کارمندان) است. اگر بخواهیم 6 بعد رضایت شغلی شامل نظام پرداخت، نوع شغل، فرصت­های پیشرفت، جوّ سازمانی، سبک رهبری و شرایط فیزیکی را به‌صورت همزمان در بین افراد که در سمت‌ها مختلف (مدیران ارشد، مدیران رده میانی و کارمندان) مشغول به کار هستند مقایسه کنیم بایست از آزمون آنالیز واریانس چندمتغیره استفاده کنیم. زیرا در این مورد 6 متغیر وابسته و یک متغیر مستقل داریم.چنانچه بیش از یک متغیر مستقل داشته باشیم مثلا بخواهیم میزان رضایت شغلی را در بین زنان و مردانی که در سمت‌ها مختلف (مدیران ارشد، مدیران رده میانی و کارمندان) مشغول به کار هستند مقایسه کنیم دو متغیر مستقل جنسیت و سمت کاری را داریم که برای آزمون فرضیه تحقیق بایست از آزمون آنالیز واریانس 2‌طرفه استفاده نمود.نکته آخر این‌که حتما فرضیه تحقیق به درستی نوشته شود. در آزمون آنالیز واریانس اختلاف میانگین متغیر وابسته (کمی پیوسته) در رده‌های متغیر مستقل (کیفی اسمی یا رتبه‌ای) بررسی می‌شود و فرضیه تحقیق باید به صورت زیر نوشته شود:متغیر وابسته (مثال: رضایت شغلی) در میان رده‌های متغیر مستقل (مثال: مدیران ارشد، مدیران رده میانی و کارمندان) تفاوت معناداری دارد.آنالیز واریانس یک طرفه(یک راهه)یکی از مباحث اولیه آمار است. افرادی که رشته آمار را تحصیل می کند این عنوان به عنوان یکی از مباحث اولیه در نظر گرفته می شود. در بسیاری از موارد همین موضوع ابتدایی دچار مشکلاتی خواهد شد. برای اینکه بتوانید فردی را در کنار خود داشته باشید ما برای شما امکانی را فراهم کرده ایم که با مجرب ترین متخصصان علم آمار ارتباط برقرار کرده و مشکلات خود را با آن ها در میان بگذارید. برای استفاده از این قابلیت در بخش مشاوره آماری رایگان می توانید استفاده کنید.در کنار آنالیز واریانس یک طرفه بسیاری از مباحث دیگری از آمار وجود دارد که برای با خبر شدن از جدید ترین آن ها و همچنین ارتباط راحت تر با شرکت آمار پیشرو می توانید صفحه اینستاگرامی آمار پیشرو را دنبال کنید.آنالیز واریانس یک طرفه (یک راهه) کاربرد های متنوعی دارد، یکی از این کاربرد ها در فصل چهارم پایان نامه است در بسیاری از موارد دانشجویان رشته های مختلف می توانند از شرکت های مختلف آماری برای انجام تحلیل آماری پایان نامه استفاده کنند. به همین منظور شما می توانید با خدمات شرکت آماری آمار پیشرو در قسمت تحلیل آماریببینید و با توجه به آن ها می توانید در قسمت ثبت سفارش فرم مورد نظر را تکمیل کرده و پروژه را به این شرکت آماری بسپارید.