آنالیز واریانس دوطرفه چیست؟-اجرای آن در SPSS با مثالی کاربردی

[block id=”breadcrumb”]

آنالیز واریانس دوطرفه یکی از مباحث آمار پارامتری است، برای فهم بهتر این مفهوم ابتدا بهتر است مطلب واریانس چیست را مطالعه کنید. آنالیز واریانس دو طرفه یکی از خدمات تحلیل آماری است که شرکت آمار پیشرو ارائه می دهد. برای توضیح این مفهوم ابتدا توضیح بسیار مختصری از آنالیز واریانس یک طرفه ارائه می دهیم و پس از آن با بیانی ساده و با مثالی ملموس به توضیح مفهوم آنالیز واریانس دوطرفه می پردازیم. در ادامه این مقاله با یک مثال کاربردی به اجرای آنالیز واریانس دوطرفه در SPSS و ارائه گزارشات پرداخته شده است. در آنالیز واریانس یک‌طرفه، اثر یک متغیر مستقل (عامل) را که دارای چند گروه است بر یک متغیر وابسته بررسی می‌کنیم.

این بررسی از طریق مقایسه میانگین متغیر وابسته در گروه‌های آن عامل انجام می‌شود. مثلاً فرض کنید می‌خواهیم بدانیم آیا سطح تحصیلات کارمندان شاغل در یک سازمان (عامل) بر میزان حقوق آنان (متغیر وابسته) تأثیر دارد. در این صورت از آنالیز واریانس یک طرفه استفاده می‌کنیم. اما اگر بخواهیم تأثیر هم‌زمان دو عامل را بر یک متغیر وابسته بررسی کنیم چطور؟ مثلاً فرض کنید در مثال حاضر بخواهیم هم‌زمان اثر سطح تحصیلات و بخش کاری کارمندان را بر میزان حقوق بسنجیم باید از چه آزمونی استفاده کنیم؟ در این حالت می‌توانیم از آنالیز واریانس دوطرفه استفاده کنیم.

آنال

آنالیز واریانس دوطرفه به زبان ساده

آنالیز واریانس دوطرفه تفاوت‌های میانگین بین گروه‌هایی را که در بین دو متغیر مستقل (عامل) تقسیم شده‌اند مقایسه می‌کند. هدف اولیه از آنالیز واریانس دوطرفه فهمیدن آن است که آیا اثر متقابل بین دو متغیر مستقل بر روی متغیر وابسته معنی‌دار است یا خیر. به عنوان مثال می‌توانیم از آنالیز واریانس دوطرفه برای بررسی این که آیا اثر متقابل بین جنسیت و سطح تحصیلات بر آزمون اضطراب دانشجویان وجود دارد استفاده کنیم که در آن جنسیت (مرد/زن) و سطح تحصیلات (لیسانس/تحصیلات تکمیلی) متغیرهای مستقل هستند و آزمون اضطراب متغیر وابسته است.

هم چنین ممکن است بخواهیم تعیین کنیم آیا اثر متقابل بین سطح فعالیت بدنی و جنسیت بر کلسترول خون در کودکان وجود دارد یا خیر، که در آن فعالیت بدنی (کم/متوسط/زیاد) و جنسیت (دختر/پسر) متغیرهای مستقل و مقدار کلسترول، متغیر وابسته هستند. اصطلاح اثر متقابل در تحلیل واریانس دوطرفه به ما می‌گوید آیا اثر یکی از متغیرهای مستقل بر متغیر وابسته به ازای همگی مقادیر متغیر مستقل دیگر یکسان است یا خیر (و همین‌طور برای متغیر مستقل دیگر). به عنوان مثال، آیا اثر جنسیت (مرد/زن) بر آزمون اضطراب تحت تأثیر سطح تحصیلات (لیسانس/تحصیلات تکمیلی) قرار دارد؟ علاوه بر این، اگر یک اثر متقابل معنی‌دار پیدا شود، احتیاج داریم تعیین کنیم آیا اثرات اصلی ساده معنی‌دار هستند؟ (این مورد در ادامه‌ی بحث شرح داده می‌شود.)

شرایط داده‌ها برای آنالیز واریانس دوطرفه

برای انجام آنالیز واریانس دوطرفه، داده‌ها باید دارای شش شرط (پذیره) زیر باشند. البته در داده‌های واقعی ممکن است تعدادی از این پذیره‌ها برقرار نباشند، که در این صورت راه‌حل‌هایی برای آن وجود دارد. ابتدا شش شرط را شرح می‌دهیم:

1. متغیر وابسته باید پیوسته باشد.
2. دو متغیر مستقل باید شامل دو یا تعدادی بیشتر از سطوح (گروه) باشند.
3. مشاهدات مستقل باشند. یعنی هیچ ارتباطی بین مشاهدات در هر گروه یا بین‌ گروه‌ها وجود نداشته باشد. به عنوان مثال، شرکت‌کنندگان متفاوت در هر گروه نباید در هیچ یک از گروه‌های دیگر حضور داشته باشند. این امر بیشتر به طرح مطالعه بستگی دارد و نیاز به آزمون خاصی برای بررسی آن وجود ندارد. اگر مطالعه دارای این شرط نباشد، آن گاه باید از آزمونی متفاوت برای آن استفاده کرد (مثلاً طرح اندازه‌های مکرر).
4. داده پرت وجود نداشته باشد.
5. متغیر وابسته باید به طور تقریبی دارای توزیع نرمال باشد. البته آنالیز واریانس دوطرفه نسبت به عدم برقراری شرط نرمال بودن، کاملاً استوار است. این یعنی پذیره‌ی نرمال بودن می‌تواند تا حدودی نقض شود و در عین حال نتایج بدست‌آمده معتبر باشد.
6. برای ترکیبات مختلف از گروه‌های دو متغیر مستقل باید همگنی واریانس وجود داشته باشد. برای بررسی آن می‌توان از آزمون لون (Levene) استفاده کرد.

در ادامه یک مثال ملموس از آنالیز واریانس دو طرفه را در نرم افزار SPSS اجرا کردیم. اما این نرم افزار کاربرد های فراوانی را در علم آمار دارد. چنانچه علاقه مند به حوزه آماری هستیداین نرم افزار یکی از اصلی ترین نرم افزار است. شما می توانید دوره آموزش نرم فزار SPSS را بگذرانید و در کنار انجام پروژه خود پروژه های آماری دیگر را انجام دهید.

نرم افزار SPSS چیست؟

اجرای آنالیز واریانس دوطرفه در SPSS با مثالی کاربردی

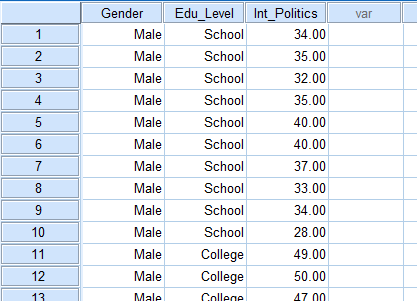
پژوهشگری می‌خواهد بررسی کند آیا علاقه فردی به موضوعات سیاسی تحت تأثیر سطح تحصیلات یا جنسیت است. به همین منظور نمونه‌ای تصادفی از شرکت‌کنندگان فراهم شد و از آنان در مورد علاقه آن به موضوعات سیاسی پرسش شد و نمره آن به صورت عددی بین صفر تا 100 ثبت شد. در این نمره‌گذاری، صفر نشان‌دهنده کم‌ترین علاقه و 100 نشان‌دهنده بیشترین علاقه است. آن گاه شرکت‌کنندگان بر حسب جنسیت (مرد/زن) و سپس تحصیلات (دبیرستان/پیش‌دانشگاهی/دانشگاه) تقسیم‌بندی شدند. بنابراین متغیر وابسته علاقه به سیاست (interest in politics) و متغیرهای مستقل جنسیت (gender) و تحصیلات (education) هستند. برای انجام این آزمون در SPSS فرض کنید داده‌ها به صورت شکل زیر هستند:در ادامه طی مراحل 14 گانه زیر نحوه انجام آنالیز واریانس دوطرفه با فرض آن که هر شش پذیره‌ی مذکور برقرار هستند شرح داده می‌شود. (1) از مسیر زیر و طبق شکل زیر پنجره مربوطه را فراخوانی می‌کنیم:

Analyze > General Linear Model > Univariate

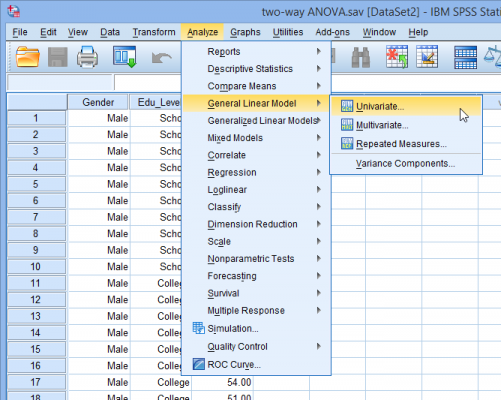
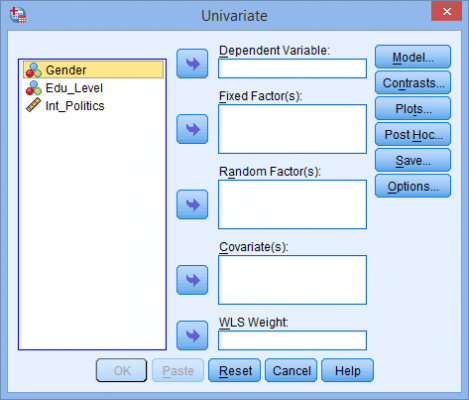
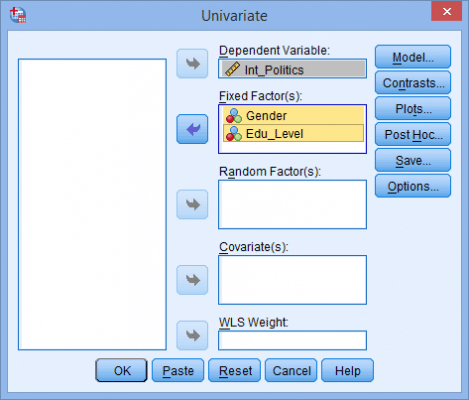
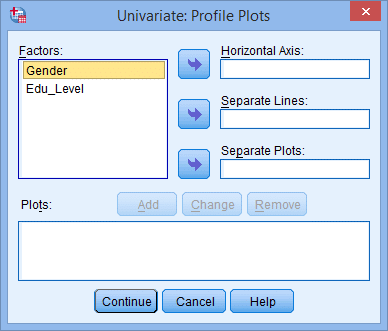
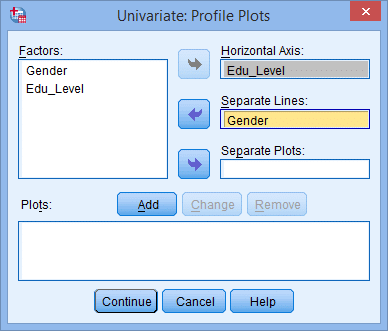
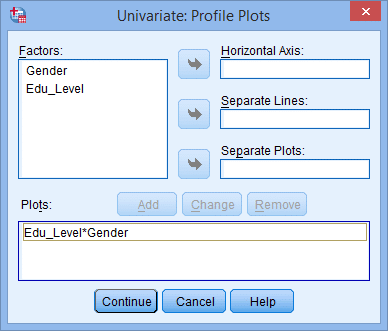
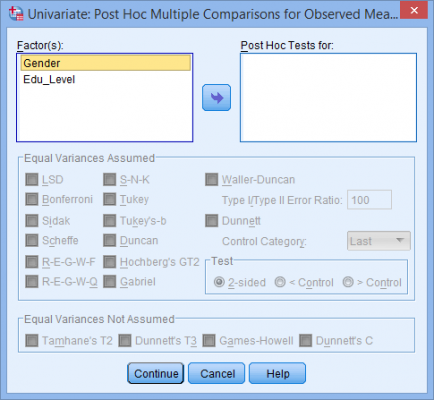
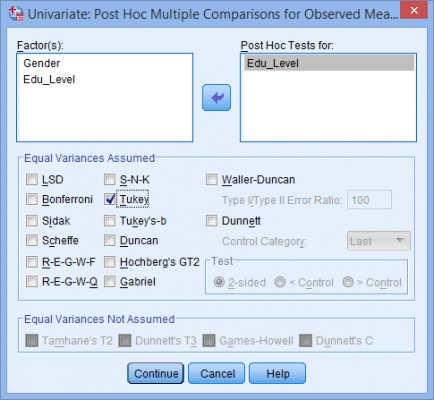
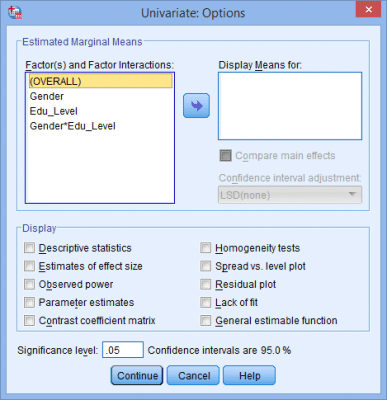
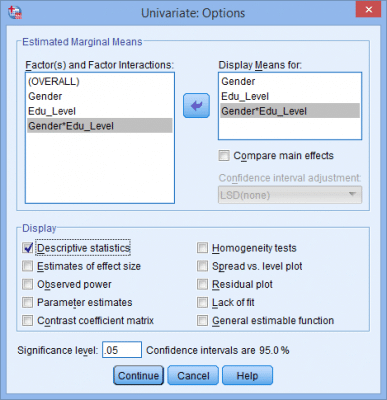
(2) در ادامه پنجره زیر ظاهر می‌شود:(3) متغیر وابسته و متغیرهای مستقل را طبق شکل زیر به قسمت‌های مربوطه منتقل می‌کنیم:(4) بر روی نمودارها (Plots) کلیک می‌کنیم و سپس پنجره زیر ظاهر می‌شود:(5) متغیر مستقل تحصیلات را از قسمت عامل‌ها (Factors) به محور افقی (Horizontal Axis) و متغیر مستقل دیگر (جنسیت) را به خطوط جداگانه (Separate Lines) منتقل می‌کنیم. این کار را مطابق شکل زیر انجام می‌دهیم:نکته 5: معمولاً متغیری را که دارای تعداد سطوح بیشتر است در محور افقی قرار می‌دهیم. (6) از کلید اضافه کردن (Add) استفاده می‌کنیم. در این صورت خواهیم دید که اثر متقابل تحصیلات و جنسیت در قسمت نمودارها (Plots) به صورت شکل زیر اضافه شده است:(7) بر روی Continue کلیک می‌کنیم. (8) بر روی آزمون‌های تعقیبی (Post Hoc) کلیک می‌کنیم. در نتیجه پنجره زیر ظاهر می‌شود:  (9) متغیر تحصیلات را از قسمت عامل‌ها (Factors) به قسمت آزمون‌های تعقیبی (Post Hoc Tests for) منتقل می‌کنیم. در این صورت قسمت Equal Variances Assumed فعال می‌شود و گزینه‌های مختلفی که برای آن‌ها می‌توان آزمون‌های تعقیبی را استفاده کرد نشان می‌دهد. در مثال حاضر، از آزمون توکی (Tukey) استفاده خواهیم کرد. نکته 6: فقط کافی است متغیرهای مستقلی را که دارای بیش از دو گروه هستند به قسمت آزمون‌های تعقیبی منتقل کنیم. به همین علت متغیر جنسیت را منتقل نکردیم. در نهایت پنجره زیر را خواهیم داشت:(10) روی Continue کلیک می‌کنیم و به پنجره تک‌متغیره (Univariate) برمی‌گردیم. (11) روی گزینه‌ها (Options) کلیک می‌کنیم و در نتیجه پنجره زیر ظاهر می‌شود:(12) متغیرهای جنسیت، تحصیلات و اثر متقابل جنسیت و تحصیلات را از قسمت Factors and Factor Interactions به قسمت Display Means for همانند شکل زیر منتقل می‌کنیم.(13) روی Continue کلیک می‌کنیم و به پنجره تک‌متغیره برمی‌گردیم. (14) روی Ok کلیک می‌کنیم و خروجی تولید می‌شود.

خروجی‌های آنالیز واریانس دوطرفه

بر اساس گزینه‌هایی که در مراحل 14 گانه قبل شرح داده شد، نتایج خروجی عبارتند از: جداول آماره‌های توصیفی، اثرات بین‌آزمودنی، آزمون‌ تعقیبی توکی (مقایسات چندگانه)  و نمودار نتایج. این نکته را نیز در نظر داشته باشید که در صورت معنی‌دار بودن اثر متقابل، باید اثرات اصلی ساده نیز گزارش شود. در مقابل، اگر اثر متقابل معنی‌دار نباشد باز هم تحلیل‌های بیشتری باید انجام شود. در این قسمت در این مورد نیز توضیح داده ایم‌شود.

جدول آماره‌های توصیفی:

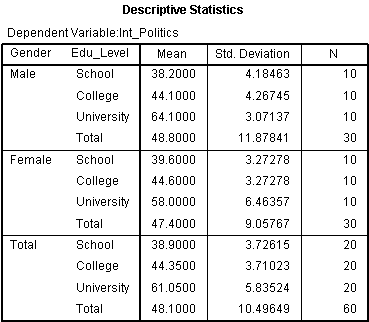
در این قسمت آماره‌های توصیفی مناسب برای گزارش یافت می‌شود:جدول فوق بسیار مفید است زیرا میانگین و انحراف معیار برای ترکیبات گروه‌ها و متغیرهای مستقل را ارائه می‌کند. هم چنین، در این جدول مجموع ردیف‌ها نیز آمده است که میانگین‌ها و انحراف معیارهای گروه‌ها را ارائه می‌کند که فقط بر حسب یکی از متغیرهای مستقل یا هیچ کدام از آن‌ها (کلی) تقسیم‌بندی شده‌اند. این آماره‌ها برای زمانی مناسب هستند که اثر متقابل معنی‌دار نشده است.

نمودار نتایج:

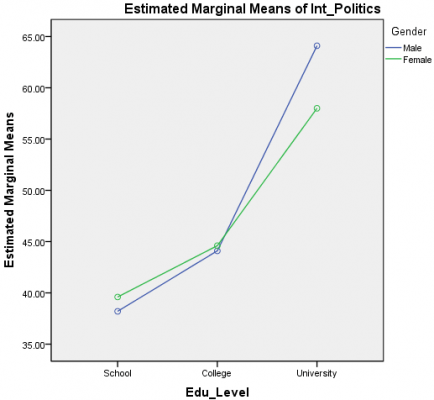
نمودار میانگین امتیازات علاقه به سیاست برای هر ترکیب گروه‌های جنسیت و تحصیلات در خطوط جداگانه ترسیم شده است:گرچه این نمودار ممکن است دارای کیفیت لازم برای نشان دادن گزارش ما نباشد، اما نمایش گرافیکی خوبی برای نتایج ارائه می‌کند. اثر متقابل معمولاً می‌تواند به صورت خطوط ناموازی دیده شود. در نمودار ما نیز می‌توان دید که دو خط نمایش داده شده موازی نیستند (خطوط یک‌دیگر را قطع می‌کنند). لذا می‌توان انتظار اثر متقابل معنی‌دار را داشت که در قسمت بعد بررسی شده است.

معنی‌داری آماری آنالیز واریانس دوطرفه:

نتایج اصلی تحلیل واریانس دوطرفه در جدول زیر (جدول اثرات بین‌آزمودنی) نشان داده می‌شود. در این جدول می‌توان دید آیا متغیرهای مستقل و اثر متقابل آن‌ها به طور آماری معنی‌دار هستند یا خیر.

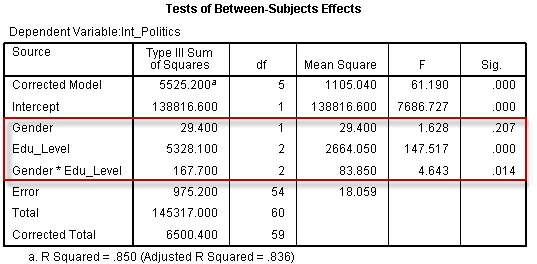
سطرهایی که مورد علاقه ما هستند سطرهای مربوط به جنیست، تحصیلات و جنسیت*تحصیلات هستند که در جدول بالا با مستطیل قرمز مشخص شده‌اند. این سطر‌ها به ما نشان می‌دهند آیا متغیرهای مستقل (جنسیت و تحصیلات) و اثر متقابل آن‌ها (جنسیت*تحصیلات) دارای اثر معنی‌دار بر متغیر وابسته هستند یا خیر. ابتدا باید به اثر متقابل نگاه و بررسی کرد آیا معنی‌دار است یا نه.

با توجه به ستون Sig در این سطر ملاحظه می‌شود که این اثر در سطح0.05 معنی‌دار است زیرا p=0.014<0.05. هم چنین می‌توان اثرات ساده جنسیت و تحصیلات را نیز گزارش کرد، اما باید با توجه به نتیجه اثر متقابل باشد. در جدول فوق می‌توان می‌توان دید که هیچ تفاوت معنی‌دار در میانگین علاقه به سیاست در بین مردان و زنان وجود ندارد (p=0.207>0.05)، در حالی که بین سطوح تحصیلات تفاوت معنی‌دار از این لحاظ وجود دارد (p<0.005).

آزمون‌های تعقیبی-اثرات اصلی ساده:

 وقتی اثر متقابل معنی‌دار داشته باشیم، گزارش اثرات اصلی می‌تواند گمراه‌کننده باشد. لذا باید اثرات اصلی ساده را نیز گزارش کرد. در مثال ما، این امر شامل تعیین تفاوت میانگین در علاقه به سیاست بین جنسیت در هر سطح تحصیلات و هم چنین سطح تحصیلات برای هر جنسیت می‌شود. متأسفانه، نرم‌افزار SPSS اجازه انجام این کار را با استفاده از رابط گرافیکی خود نمی‌دهد و برای این کار نیاز به نوشتن syntax داریم. اما وقتی اثر متقابل معنی‌دار نباشد، دو گزینه را می‌تواینم استفاده کنیم که در ادامه شرح داده می‌شود.

جدول مقایسات چندگانه:

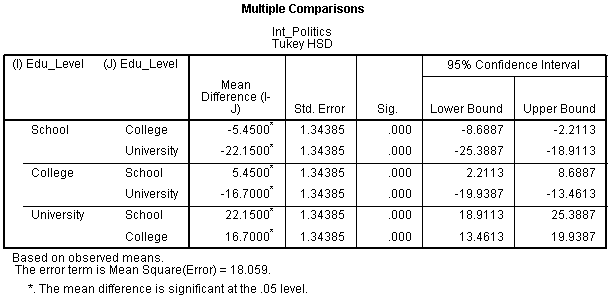
اگر اثر متقابل معنی‌دار نداشته باشیم، می‌توانیم نتایج آزمون تعقیبی توکی را برای سطوح مختلف تحصیلات گزارش کنیم که در جدول زیر آمده‌اند:در جدول فوق می‌توان دید برخی از نتایج تکرار شده‌اند، اما در نهایت چون سه سطح برای تحصیلات داریم، کافی است سطور مربوط به این تفاوت‌ها را بررسی کنیم: (1) دبیرستان و پیش‌دانشگاهی، (2) دبیرستان و دانشگاه، و (3) پیش‌دانشگاهی و دانشگاه. از این نتایج می‌توان دید که برای همگی این سطوح، تفاوت معنی‌دار وجود دارد زیرا برای همه آن‌ها p<0.0005.

تفسیر نتایج تحلیل واریانس دوطرفه:

ابتدا باید نتایج اثر متقابل گزارش شود. به عنوان مثال می‌توان نوشت: به منظور بررسی اثر جنسیت و تحصیلات بر علاقه به سیاست  یک تحلیل واریانس دوطرفه انجام شد. اثر متقابل بین جنسیت و تحصیلات بر علاقه به سیاست معنی‌دار است (F_2,54=4.643 و p=0.14). هم چنین اثر اصلی تحصیلات بر علاقه به سیاست نیز معنی‌دار است (F_2,54=2664.05 و p<0.0005)، اما اثر اصلی جنیست معنی‌دار نیست (F_1,54=29.40 و p=0.21). درادامه با توجه به نتایج آزمون تعقیبی توکی برای اثر تحصیلات چنین مشخص شد که تفاوت بین میانگین تمامی جفت‌های سطح تحصیلات معنی‌دار است (p<0.0005).

در این مطلب سعی کردیم کلیه مطالب مربوط به آنالیز واریانس دو طرفه را پوشش دهیم. اما چنانچه پروژه ای دارید و در برخی قسمت ها با مشکل مواجه شده اید. در سایت آمار پیشرو قسمتی را برای شما در نظر گرفته ایم تا بتوانید به صورت رایگان با مشاوران با تجربه این حوزه ارتباط برقرار کنید به این منظور به قسمت مشاوره آماری رایگان رفته و فرم مربوطه را پر کنید تا کارشناسان ما در اولین فرصت با شما تماس بگیرند.

اگر علاقه مند به مباحث آماری هستید می توانید صفحه آمار پیشرو در اینستاگرام را دنبال کنید تا از جدید ترین مطالبی که بر روی سایت آمار پیشرو قرار میگیرد با خبر شوید.

از جمله خدمات شرکت آمارپیشرو، اجرای آنالیز واریانس دوطرفه در طرح‌های پژوهشی و پایان‌نامه‌های دانشجویی است. برای بهره‌گیری از این خدمات، می‌توانید به سایت شرکت آمارپیشرو مراجعه کنید.