تحلیل واریانس چیست؟-آماره فیشر

[block id=”breadcrumb”]

تحلیل واریانس یکی از مباحث پر تکرار آماری است. در این مقاله قصد داریم ابتدا تحلیل وارینس را با مثالی ملموس و ساده توضیح دهیم و کاربرد آن را مطرح خواهیم کرد. در ادامه آزمون فیشر و تاثیر آن در آنالیز واریانس یکطرفه مطرح خواهد شد. در انتها هم علت استفاده از واریانس را در آزمون میانگین ها مطرح خواهیم کرد.

تحلیل واریانس چیست؟

فرض کنید می‌خواهیم در یک سازمان اداری بررسی کنیم آیا سطح تحصیلات بر میزان حقوق دریافتی تأثیر دارد. چون میزان حقوق، متغیری کمی و سطح تحصیلات متغیری کیفی است، برای این مسئله می‌توانیم از تحلیل واریانس (آنوا یا ANOVA) استفاده کنیم. برای این کار ابتدا میانگین میزان حقوق دریافتی را در هر یک از سطوح تحصیلات در نظر می‌گیریم. سپس توسط تحلیل واریانس بررسی می‌کنیم آیا میانگین‌های حقوق در سطوح تحصیلی مختلف با هم متفاوت هستند یا خیر.در صورت پذیرش فرضیه عدم برابر بودن میانگین‌های حقوق در سطوح مختلف تحصیلی، می‌توانیم نتیجه بگیریم سطح تحصیلات بر میزان حقوق دریافتی تأثیر دارد. در حقیقت با استفاده از تحلیل واریانس می‌توان بررسی آیا میانگین متغیر پاسخ در سطوح عامل مورد نظر دارای تفاوت هستند یا خیر.اما تحلیل واریانس شامل انواع بسیار زیادی است. معروف‌ترین انواع تحلیل واریانس، تحلیل واریانس یک‌طرفه و تحلیل واریانس دوطرفه است. تحلیل واریانس  از آزمون‌‌های فیشر (F) برای بررسی برابر بودن میانگین‌ها استفاده می‌کند که متعلق به سه یا تعدادی بیشتر از گروه‌ها هستند. در این مطلب، به تعدادی از سوالات مربوط به آزمون‌های فیشر (Fisher test) پاسخ می‌دهیم که برای بسیاری از محققین مورد ابهام است. سوالاتی از قبیل:

• آزمون فیشر چگونه عمل می‌کند؟
• چرا از آنالیز واریانس‌ها برای آزمون میانگین‌ها استفاده می‌کنیم؟

در این مطلب از مفاهیم و نمودارهای مختلف برای پاسخ به سوالات فوق در قالب آنالیز واریانس یک‌طرفه استفاده می‌کنیم.

آزمون فیشر و آماره های فیشر چیست؟

عبارت آزمون فیشر بر اساس این حقیقت است که این آزمون‌ها از آماره فیشر برای آزمون فرضیات استفاده می‌کنند. آماره فیشر برابر با نسبت دو واریانس است و از نام دانشمند آمارشناس، رونالد فیشر برگرفته شده است. واریانس‌ها پراکندگی داده‌ها در اطراف میانگین را اندازه‌گیری می‌کنند. واریانس‌های با مقدار بیشتر وقتی اتفاق می‌افتند که نقاط داده‌ها تمایل به قرارگیری در فواصل دورتری از میانگین را داشته باشند.اما تفسیر واریانس‌ها به طور مستقیم کار مشکلی است، زیرا واحد اندازه‌گیری آن‌ها مجذور (توان دوم) واحد اندازه‌گیری داده‌ها است. اگر جذر واریانس را در نظر بگیریم، انحراف معیار به دست می‌آید که تفسیر آن ساده‌تر است زیرا واحد اندازه‌گیری آن با واحد داده‌ها یکسان است. گرچه تفسیر واریانس‌‌ها به طور مستقیم سخت است، اما در برخی آزمون‌های آماری از آن‌ها استفاده می‌شود.آماره فیشر نسبت دو واریانس، یا به طور دقیق‌تر، نسبت دو میانگین مربعات (mean squares) است. میانگین مربعات همان واریانس است که بر درجات آزادی تقسیم شده، همان درجات آزادی که برای براورد واریانس به کار گرفته شده است.حال بیایید دقیق‌تر نگاه کنیم. واریانس، مجموع مربعات انحرافات از میانگین است. هر چه نمونه‌ بزرگ‌تری داشته باشیم، تعداد بیشتری مربع انحرافات برای جمع کردن داریم. نتیجه آن که هر چه مشاهدات بیشتری را اضافه کنیم، این مجموع بزرگ‌تر می‌شود. با به کارگیری درجات آزادی، میانگین‌ مربعات نیز نقش ایفا می‌کند. میانگین مربعات، تفاضل براورد هر اندازه‌گیری از واریانس را با توجه به تعداد اندازه‌گیری‌ها محاسبه می‌کند. اگر از میانگین مربعات استفاده نکنیم، واریانس‌ها قابل مقایسه نیستند و نسبت واریانس‌ها برای آماره فیشر منطقی نخواهد بود.با توجه به این که آزمون‌های فیشر نسبت دو واریانس را ارزیابی می‌کنند، ممکن است فکر کنیم تنها برای بررسی برابری واریانس‌ها به کار می‌آیند. اما در حقیقت آزمون‌های فیشر برای کارهای بیشتری نیز قابل استفاده هستند. آزمون‌های فیشر به طور جالبی انعطاف‌پذیرند، چون می‌توان واریانس‌های مختلفی را در آن‌ها به کار برد و انواع مختلفی از فرضیات را آزمون کرد. آزمون‌های فیشر می‌توانند برای مقایسه برازش مدل‌های مختلف، آزمون معناداری کلی مدل‌های رگرسیون، آزمون جملات خاص در مدل‌های خطی و بررسی برابری مجموعه‌ای از میانگین‌ها به کار روند.

آزمون فیشر در آنالیز واریانس یک‌طرفه

در آنالیز واریانس یک‌طرفه آزمون می‌کنیم آیا مجموعه‌ای از میانگین‌ها با هم برابرند یا خیر. برای آن که از آزمون فیشر برای این منظور استفاده کنیم، باید از واریانس‌های مناسب در نسبت استفاده کنیم. آماره فیشر در آنالیر واریانس یک‌طرفه بدین صورت تعریف می‌شود:

برای این که ببینیم آزمون‌های فیشر چگونه عمل می‌کنند، از یک مثال آنالیز واریانس یک‌طرفه استفاده می‌کنیم. فرض کنید در مطالعه‌ای یک عامل داریم و می‌خواهیم اثر آن را بر یک متغیر پاسخ کمّی بررسی کنیم (آنالیز واریانس یک طرفه چیست؟-با مثال کاربردی در SPSS). عامل مورد نظر دارای چهار گروه و حجم نمونه 40 است. پس از اجرای تحلیل واریانس، نتایج آن به شکل زیر شده است:

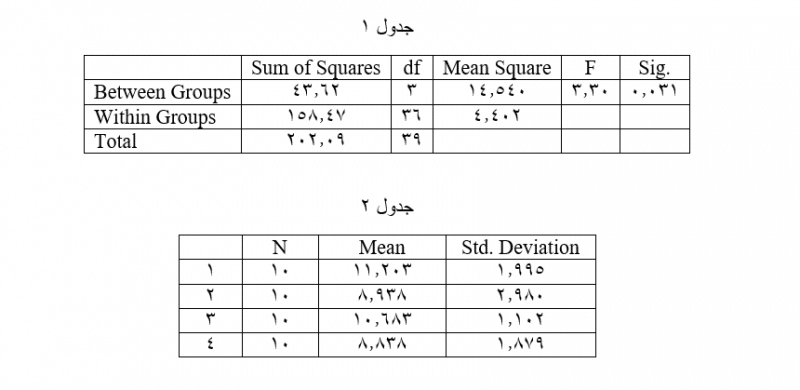
صورت کسر آماره فیشر (واریانس بین‌گروهی)

در تحلیل واریانس یک‌طرفه، میانگین هر یک از چهار گروه عامل محاسبه می‌شود که طبق جدول 2 عبارتند از: 11.203، 8.983، 10.683 و 8.838. میانگین‌های این گروه‌ها حول میانگین کلی (9.915) که از 40 مشاهده حاصل شده قرار گرفته‌اند.هر چه قدر این گروه‌ها دارای فاصله بیشتری از میانگین کلی باشند، واریانسی که در صورت کسر آماره فیشر قرار دارد، بزرگ‌تر می‌شود.راحت‌تر است آن است که بگوییم میانگین‌های گروه‌ها زمانی تفاوت معنی‌دار دارند که از یک‌دیگر دورتر باشند. این مسئله در آزمون فیشر به صورت بزرگ‌تر بودن واریانس در صورت کسر لحاظ می‌شود.برای درک بهتر این مطلب، نمودار زیر را ببینید. این نمودار دارای دو قسمت مجزا است که برای مقایسه دو حالت با یک‌دیگر در قالب یک نمودار آمده‌اند: یک حالت برای واریانس کوچک و حالت دیگر برای واریانس بزرگ. در هر کدام از این دو حالت، چهار نقطه قرار دارند که میانگین هر یک از چهار گروه هستند. همان طور که می‌بینیم، در حالت واریانس کوچک، نقاط نمودار (میانگین‌های گروه‌ها) دارای فواصل کم‌تری نسبت به یک‌دیگر هستند تا حالت واریانس بزرگ که نقاط نمودار با فواصل بیشتری نسبت به هم قرار گرفته‌اند.

حال مجدداً به خروجی تحلیل واریانس یک‌طرفه مراجعه می‌کنیم. باید کدام آماره را برای واریانس بین‌گروهی استفاده کنیم؟ این آماره در جدول یک، به صورت مربع میانگین واقع در سطر Between Groups یعنی عدد 13.394 است. این عدد، مجموع مربع فاصله‌ها از میانگین کلی است که تقسیم بر درجات آزادی عامل شده‌ است. هر چه میانگین‌‌های گروه‌های عامل از یک‌دیگر فاصله بیشتری بگیرند، این عدد نیز افزایش می‌یابد.

مخرج کسر آماره فیشر (واریانس درون‌گروهی)

حال مخرج کسر آماره فیشر را بررسی می‌کنیم که واریانس‌های داخل هر گروه را در نظر می‌گیرد. این واریانس درون‌گروهی، فاصله بین هر مشاهده با میانگین گروه مربوط به آن مشاهده را اندازه‌گیری می‌کند، فاصله بدست‌آمده را به توان دو می‌رساند و همه آن‌ها را با هم جمع می‌کند و در نهایت بر درجات آزادی خطا تقسیم می‌کند.هر چه مشاهدات داخل هر گروه به میانگین گروه مربوط به خود نزدیک‌تر باشند، واریانس درون‌گروهی کوچک‌تر می‌شود. برعکس هر چه مشاهدات داخل هر گروه از میانگین مربوط به خود دورتر باشند، واریانس درون‌گروهی افزایش می‌یابد.در نمودار زیر واریانس درون‌گروهی کوچک با واریانس درون‌گروهی بزرگ مقایسه شده است. منحنی‌های این نمودار نشان می‌دهند مشاهدات نمونه درون هر گروه چه قدر فشرده در اطراف میانگین آن گروه قرار گرفته‌اند. مخرج کسر آماره فیشر، یا همان واریانس درون‌گروهی، در قسمت راست نمودار زیر بزرگ‌تر است، زیرا مشاهدات نمونه در فواصل بیشتری نسبت به میانگین گروه قرار دارند.

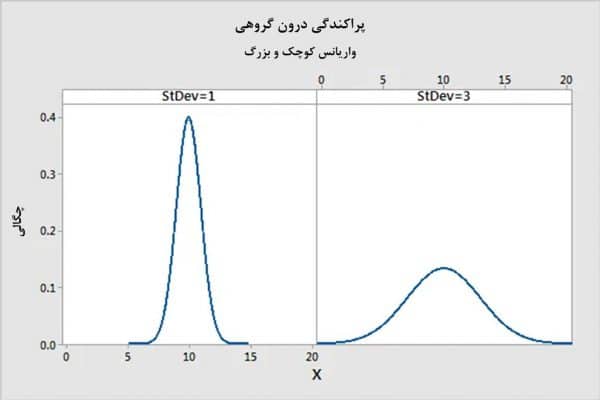
برای آن که نتیجه بگیریم میانگین‌های گروه‌ها برابر نیستند، باید واریانس درون‌گروهی کوچک باشد. چرا؟ چون واریانس درون‌گروهی نشان‌دهنده واریانسی است که توسط مدل تبیین نشده است. در آمار این واریانس را خطای تصادفی می‌نامند. هر چه خطا افزایش یابد، احتمال بیشتری وجود دارد که تفاوت‌های مشاهده‌شده بین میانگین‌های گروه‌ها به جای آن که از تفاوت‌های واقعی در گروه‌های جامعه ناشی شده باشد، به علت خطا به وجود آمده باشند. لذا واضح است که ما به دنبال مقادیر کم‌تری از خطا هستیم!حال بیایید دوباره به خروجی تحلیل واریانس یک‌طرفه نگاه کنیم. واریانس درون‌گروهی که در جدول 1 به نمایش درآمده برابر با 4.402 است.

آماره فیشر (نسبت واریانس بین‌گروهی به واریانس درون‌گروهی)

همان طور که گفتیم، آماره‌های فیشر نسبت دو واریانس هستند. اگر فرضیه صفر درست باشد، مقدار آماره فیشر تقریباً برابر با یک می‌شود (برای دانستن فرضیات صفر و یک به مقاله آنالیز واریانس یک طرفه مراجعه کنید). فرضیه صفر در آنالیز واریانس یک‌طرفه، به صورت عدم معنی‌داری عامل است.در نمودار قبل، دو مقدار متفاوت واریانس را که در یک آماره آزمون فیشر تحلیل واریانس یک‌طرفه به کار رفته‌اند دیدیم. حال این دو را کنار هم قرار ‌می‌دهیم و می‌بینیم ترکیب آن‌ها دو آماره فیشر کوچک و بزرگ را تولید می‌کند. در نمودارهای زیر گستره میانگین‌های گروه‌ها با گستره مشاهدات نمونه در داخل هر گروه قابل مقایسه است.

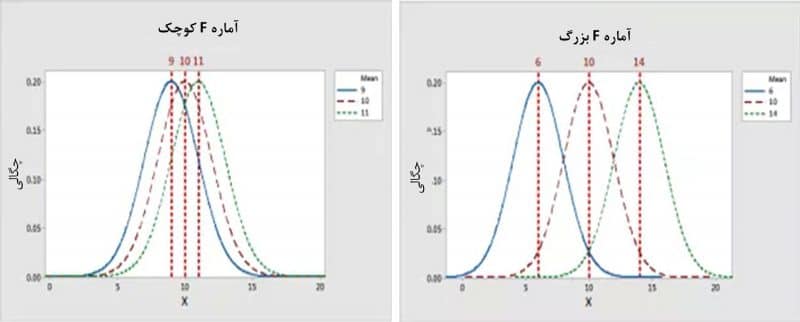
گراف سمت چپ (مقدار کوچک F): میانگین‌های گروه‌ها نسبت به پراکندگی درون‌گروهی با فشردگی بیشتری کنار هم قرار گرفته‌اند. فاصله بین میانگین‌ها نسبت به خطای تصادفی درون هر گروه، کوچک است. بنابراین نمی‌توان نتیجه گرفت این گروه‌ها واقعاً در جامعه نیز متفاوت هستند.گراف سمت راست (مقدار بزرگ): میانگین گروه‌ها نسبت به پراکندگی مشاهدات درون هر گروه بیشتر گسترده شده‌اند. در این حالت، احتمال زیادی وجود دارد که تفاوت‌های مشاهده‌شده بین میانگین‌های گروه‌ها واقعاً نشان‌دهنده تفاوت در سطوح جامعه باشند.

چگونگی محاسبه مقدار آماره فیشر

با مراجعه به خروجی مثال، می‌توانیم صورت و مخرج کسر آماره فیشر را به صورت زیر محاسبه کنیم:

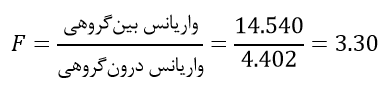
حال برای این که نتیجه بگیریم میانگین‌های گروه‌ها با هم برابر نیستند، باید مقدار آماره فیشر به اندازه کافی بزرگ باشد تا بتوانیم فرضیه صفر را رد کنیم. نکته قابل توجه در مورد آماره فیشر آن است که آماره‌ای فاقد واحد اندازه‌گیری است و این موضوع تفسیر آن را ساده می‌کند.مقدار آماره فیشر ما برابر با 3.30 شد که یعنی واریانس بین‌گروهی 3.3 برابرِ واریانس درون‌گروهی است. اما فرضیه صفر معادل با آن است که نسبت این واریانس‌ها برابر است که یعنی مقدار آماره فیشر برابر با یک می‌شود. بنابراین آیا آماره فیشری با مقدار 3.3 به اندازه کافی بزرگ است که فرضیه صفر را رد کنیم؟همان طور که می‌دانید، مقدار آماره فیشر را باید با مقادیر بحرانی جدول فیشر مقایسه کنیم. مقدار بحرانی جدول فیشر با درجات آزادی صورت 3 و درجات آزادی مخرج 36 (جدول 1) و با مقدار آلفای 0.05 برابر با 2.87 است. البته همان طور که اطلاع دارید، از جدول فیشر زمانی استفاده می‌شود که به طور دستی محاسبات را انجام می‌دهیم. زمانی که از نرم‌افزار استفاده می‌کنیم از p-مقدار یا sig استفاده می‌کنیم که توسط نرم‌افزار محاسبه می‌شود. در این مثال، مقدار sig برابر با 0.031 است که چون کوچک‌تر از 0.05 است باز هم فرضیه صفر رد می‌شود.

بالاخره چرا از واریانس‌ برای آزمون میانگین‌ها استفاده می‌کنیم؟

برگردیم به سوالی که در ابتدا در مورد تحلیل واریانس‌ها برای بررسی تفاوت میانگین‌های گروه‌ها مطرح کردیم. روی این جمله تمرکز می‌کنیم: «میانگین‌ها متفاوت هستند». این مسئله دقیقاً شامل پراکندگی میانگین‌های گروه‌ها است. اگر هیچ پراکندگی در میانگین‌ها وجود نداشته باشد، نمی‌توانند متفاوت باشند. به طور مشابه، هر چه تفاوت‌های بین میانگین‌ها بیشتر باشد، پراکندگی بیشتری نیز وجود خواهد داشت.آزمون‌های فیشر در مطالعات تحلیل واریانس، مقدار پراکندگی بین میانگین‌های گروه‌ها را بررسی می‌کنند. این بررسی بدین صورت است که در آن پراکندگی درون‌گروهی برای تعیین وجود تفاوت معنی‌دار بین میانگین‌های گروه‌ها به کار می‌رود. البته نتایج آزمون فیشر در صورتی که نشان‌دهنده تفاوت معنی‌دار بین میانگین‌های گروه‌ها باشد، فقط می‌گوید همه میانگین‌ها برابر نیستند. اما نمی‌تواند بگوید کدام میانگین‌ها برابر نیستند، برای این کار می‌توان از آزمون‌های تعقیبی استفاده کرد.در این مطلب سعی شد به تدوین خود مفهوم آنالیز واریانس پرداخته شود. در ادامه یکی از انواع تحلیل واریانس یعنی آماره فیشر نیز بررسی شد و همچنین در آینده مطالبی دیگر درباره آنالیز واریانس منتشر خواهد شد. چنانچه به مسائل آماری علاقه مندید میتوانید صفحه اینستاگرام آمار پیشرو را دنبال کنید و از جدید ترین مباحثی که منتشر می کنیم با خبر شوید.امیدواریم مطلب جامع و کامل برای شما ارائه اما چنانچه نارسایی در تحلیل واریانس احساس کردید می توانید در قسمت نظرات سوالات خود را مطرح کنید.چنانچه  به صورت اختصاصی تر می خواهید به سوالات شما پاسخ داده شود متخصصین ما آماده اند تا تجربه چندین ساله خود را در اختیار شما قرار دهند، به منظور بهره مندی از این خدمات در قسمت مشاوره آماری رایگان می توانید پرسش های خود را مطرح کنید.با توجه به کاربرد های مختلفی که تحلیل واریانس در بخش های علمی و غیر علمی دارد، چنانچه به منظور انجام تحلیل واریانس نیاز به کمک متخصصان دارید این خدمات را شرکت های آماری ارائه می دهند. یکی از این شرکت ها که با بهره گیری از افراد متخصص خدمات با کیفیتی را ارائه می دهد شرکت آمار پیشرو است.