مانوا یا تحلیل واریانس چند متغیره (MANOVA) درSPSS

[block id=”breadcrumb”]

تحلیل واریانس چندمتغیره مانوا (MANOVA) در زمره روش‌های تحلیل واریانس قرار دارد.در این مقاله ابتدا مفهوم تحلیل واریانس مانوا را بررسی کرده و سپس با مثالی ملموس تحلیل واریانس چند متغیره  در SPSS اجرا کردیم.

تحلیل واریانس چند متغیره یا مانوا(MANOVA) چیست؟

به عنوان مثالی از تحلیل واریانس چندمتغیره، فرض کنید می‌خواهیم تأثیر سطح فعالیت بدنی را بر کاهش وزن و کاهش فشار خون افراد بررسی کنیم. در این حالت، فعالیت بدنی که در سه سطح کم، متوسط و زیاد سنجیده می‌شود به عنوان عامل (متغیر مستقل) است و متغیرهای کاهش وزن و کاهش فشار خون به عنوان متغیرهای وابسته هستند. چون در این مثال بیش از یک متغیر وابسته وجود دارد، باید از تحلیل واریانس چندمتغیره استفاده کنیم.

چنان‌چه تنها یک متغیر وابسته وجود داشت (مثلاً فقط کاهش وزن) آن گاه باید از تحلیل واریانس یک‌طرفه برای بررسی اثر فعالیت بدنی بر آن استفاده می‌کردیم. هم‌چنین اگر فقط یک متغیر وابسته و دو متغیر مستقل وجود داشته باشد، آن‌گاه باید از تحلیل واریانس دوطرفه بهره گرفت. مثلاً فرض کنید اگر در همین مثال قصد داشتیم اثر سطح فعالیت بدنی و گروه خونی را بر کاهش وزن افراد بررسی کنیم، آن گاه تحلیل واریانس دوطرفه گزینه مناسبی بود.

تحلیل واریانس چندمتغیره یک‌طرفه (مانوای یک‌طرفه) برای تعیین این امر استفاده می‌شود که آیا تفاوتی بین گروه‌های یک متغیر مستقل در بیش از یک متغیر وابسته پیوسته وجود دارد یا خیر. هم چنین اگر بخواهیم اثر دو متغیر مستقل را بر بیش از یک متغیر وابسته بسنجیم، آن گاه باید از مانوای دوطرفه استفاده کنیم.حتی می توانید تحلیل کواریانس چند متغیره هم ببینید.

به عنوان مثال، از مانوای یک‌طرفه برای بررسی وجود تفاوت در حافظه کوتاه‌مدت و بلندمدت دانش‌آموزان بر اساس سخنرانی‌هایی با چهار مدت زمان متفاوت می‌توان استفاده کرد. در این مثال، دو متغیر وابسته عبارتند از حافظه کوتاه‌مدت و حافظه بلندمت، در حالی که متغیر مستقل، مدت زمان سخنرانی است که با چهار زمان 30، 60، 90 و 120 دقیقه اندازه‌گیری می‌شود.

باید توجه داشت که مانوا دارای یک آماره آزمون کلی است و نمی‌تواند بگوید کدام یک از گروه‌های متغیر مستقل به طور معنی‌دار از یک‌دیگر متفاوت هستند. این آماره تنها می‌تواند بگوید حداقل دو گروه دارای تفاوت هستند. چون ممکن است سه، چهار، پنج یا تعداد بیشتری گروه در طرح آزمایش داشته باشیم، تعیین آن که کدام یک از گروه‌ها متفاوت هستند مهم است. برای همین امر می‌توان از آزمون‌های تعقیبی استفاده کرد.

در ادامه طی یک مثال، اجرای تحلیل واریانس مانوا در SPSS شرح داده می‌شود. پیش از آن، شرایطی که باید برقرار باشند تا مجاز به استفاده از آنوا باشیم، ذکر می‌شوند.

شرایط استفاده از تحلیل واریانس چند متغیره مانوا

زمانی که برای انجام تحلیل‌های خود، مانوای یک‌طرفه را انتخاب می‌کنیم، قسمتی از فرایند شامل بررسی شرایط داده‌ها است تا مطمئن شویم داده‌ها اجازه اجرای مانوا را می‌دهند. برای اجرای مانوا، باید 9 شرط که در ادامه می‌آیند برقرار باشند. البته نباید تعجب کرد اگر یک یا دو تا از این شرط‌ها در اجرای آزمایش‌های واقعی برقرار نباشند. در این صورت معمولاً راه‌حل‌های جایگزین وجود دارند.

شرایطی که باید برای اجرای تحلیل واریانس چند متغیره برقرار باشند، عبارتند از:

1- باید تعداد دو یا بیشتر متغیر وابسته داشته باشیم که هر کدام در مقیاس‌های بازه‌ای یا نسبتی اندازه‌گیری شده‌اند (یعنی کمّی باشند). مثال‌هایی از متغیرهای وابسته که دارای این شرط باشند عبارتند از: زمان تجدید نظر (اندازه‌گیری‌شده به ساعت)؛ هوش (اندازه‌گیری‌شده با استفاده از امتیاز IQ)، عملکرد در امتحان (اندازه‌گیری‌شده از صفر تا 100)؛ وزن (اندازه‌گیری‌شده به کیلوگرم).

2- متغیر مستقل حاضر در مطالعه باید شامل دو یا تعدادی بیشتری گروه باشد. به عنوان مثال‌هایی از متغیر مستقلی که دارای این شرط هستند می‌توان از این موارد نام برد: نژاد (مثلاً در سه گروه قفقازی، آفریقایی-آمریکایی و اسپانیایی)؛ سطح فعالیت بدنی (مثلاً در چهار گروه بسیار کم، کم، متوسط و زیاد)؛ شغل (مثلاً در پنج گروه جراح، دکتر، پرستار، دندان‌پزشک و درمانگر).

3- مشاهدات باید مستقل از هم باشند، یعنی هیچ رابطه‌ای بین مشاهدات در هر گروه یا بین گروه‌های مختلف نباشد. به عنوان مثال، شرکت‌کنندگان حاضر در هر گروه نباید در بیش از یک گروه حضور داشته باشند. این مسئله بیشتر مربوط به طراحی پژوهش است و برای آن آزمونی وجود ندارد، ولی شرطی مهم برای اجرای مانوا است.

4- حجم نمونه باید کافی باشد. برای مانوا باید تعداد مشاهدات در هر گروه از متغیر مستقل از تعداد متغیرهای وابسته حاضر در مطالعه بیشتر باشند.

5- نباید داده‌های پرت تک‌متغیره یا چندمتغیره وجود داشته باشند. شناسایی داده‌های پرت تک‌متغیره با نمودار جعبه‌ای و داده‌های پرت چندمتغیره با استفاده از فاصله ماهالانوبیس (Mahalanobis distance) انجام می‌شود.

6- داده‌ها باید نرمال چندمتغیره باشند. متأسفانه، نرمال بودن چندگانه شرطی بحث‌برانگیز است و در SPSS نمی‌توان آن را بررسی کرد. به جای آن، فقط نرمال بودن هر یک از متغیرهای وابسته بررسی می‌شود. برای این کار می‌توان به عنوان مثال، از آزمون شاپیرو-ویلک استفاده کرد.

7- باید رابطه‌ای خطی بین هر جفت از متغیرهای وابسته به ازای هر گروه از متغیر مستقل وجود داشته باشد. اگر متغیرها به طور خطی وابسته نباشند، توان آزمون کاهش می‌یابد. برای بررسی این شرط می‌توان از نمودار ماتریس پراکَنش برای هر گروه از متغیر مستقل استفاده کرد.

8- ماتریس‌های واریانس-کوواریانس باید همگن باشند. برای بررسی این شرط می‌توان از آزمون اِم-باکس (Box’s M test) برای برابری کوواریانس استفاده کرد. اگر داده‌ها دارای این شرط نباشند، باید آزمون همگنی لِوِن (Leven) را برای همگنی واریانس نیز اجرا کرد تا شاید بتوان دلیل عدم برقراری شرط را پیدا کرد.

9- نباید هم‌خطی وجود داشته باشد. به طور مطلوب، متغیرهای وابسته باید همبستگی متوسطی با هم داشته باشند. اگر همبستگی‌ها خیلی کم باشند، بهتر است از آنواهای جداگانه استفاده شود. اما اگر همبستگی‌ها زیاد باشند (بیشتر از 0.9)، آن گاه همخطی وجود دارد. این مسئله برای تحلیل واریانس چند متغیره مشکل‌ساز است.

برای بررسی شروط شماره 5 تا 9 مذکور در بالا می‌توان از SPSS استفاده کرد. اما پیش از آن، باید مطمئن باشیم شروط شماره 1 تا 4 برقرار هستند، که برای آن‌ها نیازی به استفاده از SPSS نیست.

تحلیل واریانس چند متغیره مانوا در spss

برای یادگیری بهتر نحوه انجام تحلیل واریانس چند متغیره، این مثال را در نظر می‌گیریم.دانش‌آموزان حاضر در یک دبیرستان از سه مدرسه ابتدایی متفاوت آمده‌اند. مدیر دبیرستان می‌خواهد بداند آیا در بین دانش‌آموزان مدارس ابتدایی مختلف به لحاظ تحصیلی تفاوت وجود دارد یا خیر. به همین منظور، تعداد 20 دانش‌آموز از مدرسه A، 20 دانش‌آموز از مدرسه B و 20 دانش‌آموز از مدرسه C انتخاب می‌شوند و عملکرد تحصیلی آن‌ها توسط نمرات پایان‌سالی که در امتحانات انگلیسی و ریاضی کسب کرده‌اند اندازه‌گیری می‌شود. بنابراین دو متغیر وابسته شامل نمره انگلیسی و نمره ریاضی وجود دارد و متغیر مستقل، مدرسه است که شامل سه گروه مدرسه A، مدرسه B و مدرسه C است.

نرم افزار SPSS چیست؟

حال برای انجام مانوا، متغیرهای حاضر در SPSS بدین صورت در نظر گرفته می‌شوند. متغیر مستقل با نام School، متغیرهای وابسته به صورت English_Score و Maths_Score هستند. پس از بررسی برقراری شروط نه‌گانه که پیشتر ذکر شد، مانوا را طی مراحل زیر در SPSS اجرا می‌کنیم.

1- از مسیر زیر، پنجره مانوا را فراخوانی می‌کنیم:

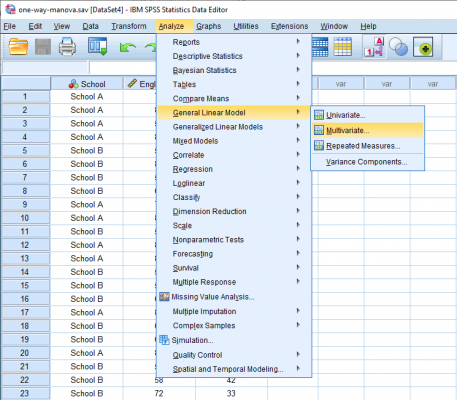
در ادامه پنجره زیر، یعنی پنجره مانوا ظاهر می‌شود:

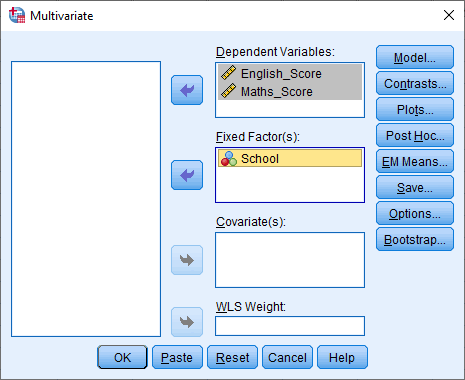
2- همانند شکل زیر، متغیر مستقل را به قسمت عامل‌های ثابت، و متغیرهای وابسته را به قسمت متغیرهای وابسته منتقل می‌کنیم:

3- حال روی گزینه Plots کلیک می‌کنیم و پنجره زیر ظاهر می‌شود:

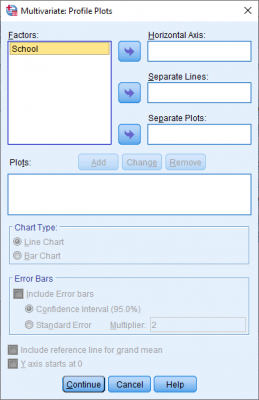
4- متغیر مستقل را به محور افقی، همانند شکل زیر منتقل می‌کنیم:

5- روی گزینه Add کلیک می‌کنیم. در این مرحله باید همانند شکل زیر، متغیر مستقل به قسمت نمودارها اضافه شده باشد:

6- روی Continue کلیک می‌کنیم و مجدداً به پنجره مانوا برمی‌گردیم.

7- حال روی Post Hoc کلیک می‌کنیم و به پنجره آزمون‌های تعقیبی همانند شکل زیر وارد می‌شویم:

8- متغیر مستقل را به قسمت آزمون‌های تعقیبی منتقل و گزینه آزمون توکی را همانند شکل فعال می‌کنیم:

نکته) می‌توان از آزمون‌های تعقیبی دیگر هم استفاده کرد که بستگی به طرح پژوهش دارد. اگر متغیر مستقل تنها دارای دو گروه باشد، احتیاج به استفاده از آزمون‌های تعقیبی نیست.

9- روی Continue کلیک می‌کنیم و مجدداً به پنجره تحلیل واریانس چند متغیره برمی‌گردیم.

10- روی EM Means کلیک می‌کنیم و همانند شکل زیر، به پنجره میانگین‌های حاشیه‌ای براوردشده می‌رویم:

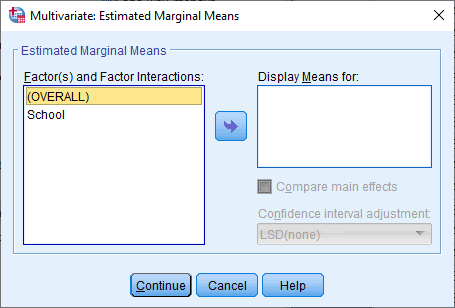
11- متغیر مستقل را از قسمت عامل‌ها به قسمت نمایش میانگین‌ها وارد می‌کنیم. این کار همانند پنجره زیر انجام می‌شود:

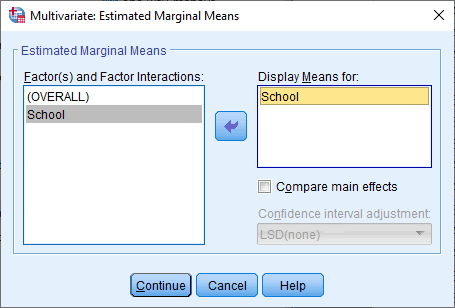
12- روی Continue کلیک می‌کنیم و باز هم به پنجره مانوا بازمی‌گردیم.

13- روی Options کلیک می‌کنیم و همانند شکل زیر، به پنجره گزینه‌های مانوا وارد می‌شویم:

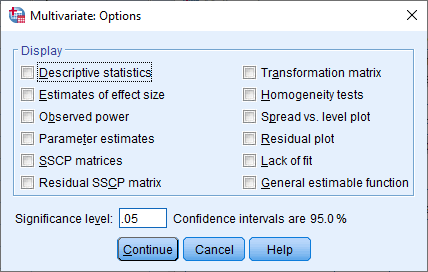
14- گزینه‌های آماره‌های توصیفی و اندازه‌اثرهای براوردشده را همانند شکل زیر فعال می‌کنیم:

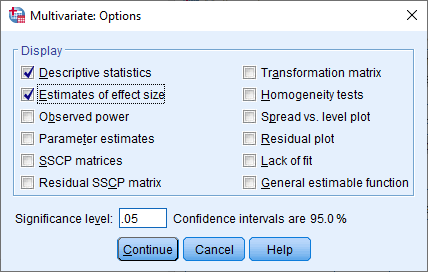
15- روی Continue کلیک می‌کنیم و به پنجره مانوا برمی‌گردیم.

16- روی OK کلیک می‌کنیم تا خروجی ظاهر شود.

تفسیر نتایج تحلیل واریانس چند متغیره

نرم‌افزار SPSS تعداد زیادی جدول برای خروجی تحلیل واریانس چند متغیره ارائه می‌کند. در این قسمت، فقط پنجره‌های اصلی که برای تفسیر نتایج مانوا احتیاج است بررسی می‌کنیم.

جدول آماره‌های توصیفی

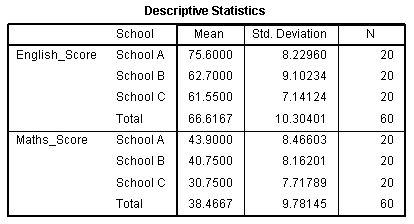
در این جدول، میانگین و انحراف معیار برای متغیرهای وابسته نمایش داده می‌شود، که توسط متغیر وابسته جدا شده‌اند. هم چنین، این جدول دارای سطرهای کل (Total) هم هست، که میانگین‌ها و انحراف معیارهای گروه‌ها را نمایش می‌دهد که فقط توسط متغیرمستقل جدا شده‌اند.

جدول آزمون‌های چندمتغیره

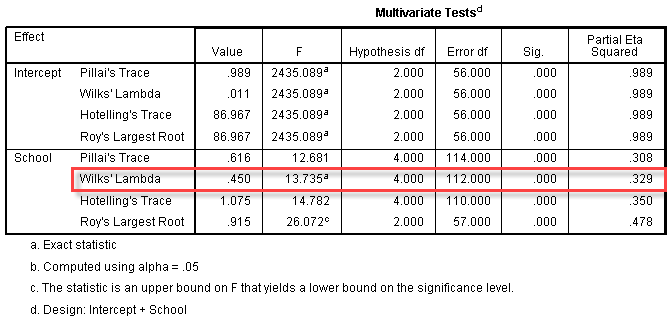
در این جدول، نتایج تحلیل واریانس چند متغیره ارائه شده است. در سطر دوم این جدول، نتیجه آزمون لامبدای ویلکس به نمایش درآمده که با مربع قرمز مشخص شده است. برای این که بدانیم آیا مانوا به طور آماری معنی‌دار است یا خیر، باید به مقدار Sig نگاه کنیم. در این جدول، مقدار Sig برابر با 0.000 شده است که کم‌تر از مقدار آلفا (0.05) و لذا معنی‌دار است. پس می‌توان نتیجه گرفت عملکرد تحصیلی دانش‌آموزانی که از مدرسه‌های ابتدایی متفاوت آمده‌اند با هم دارای تفاوت معنی‌دار است.

نتیجه به‌دست‌آمده را می‌توان بدین صورت گزارش کرد: بین عملکرد تحصیلی بر اساس مدارس قبلی دانش‌آموزان تفاوت معنی‌دار وجود دارد که در آن F (4, 112) = 13.74، p < .0005.

حال اگر آزمون معنی‌دار شده باشد (که در مثال حاضر معنی‌دار است)، باید از آزمون‌های تعقیبی نیز استفاده کرد که در ادامه خواهیم دید.

جدول آنواهای تک‌متغیره

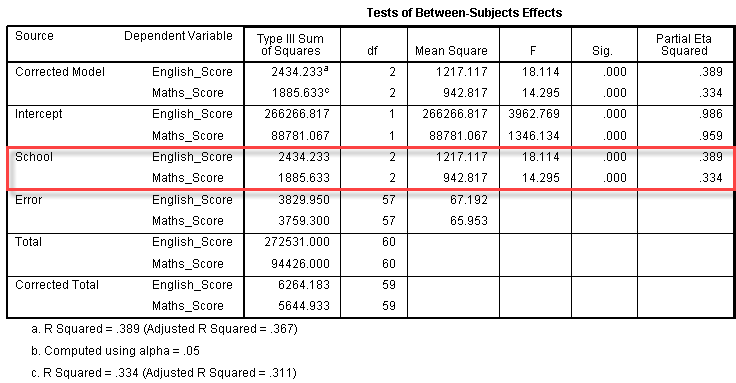
در جدول فوق، به سطرهایی که با مربع قرمز مشخص شده‌اند توجه می‌کنیم. با توجه به این سطرها می‌بینیم که مدرسه قبلی دارای اثری معنی‌دار بر هر دو متغیر وابسته نمره انگلیسی (F (2, 57) = 18.11، p < .0005) و نمره ریاضی (F (2, 57) = 14.30، p < .0005) است.

جدول مقایسات چندگانه

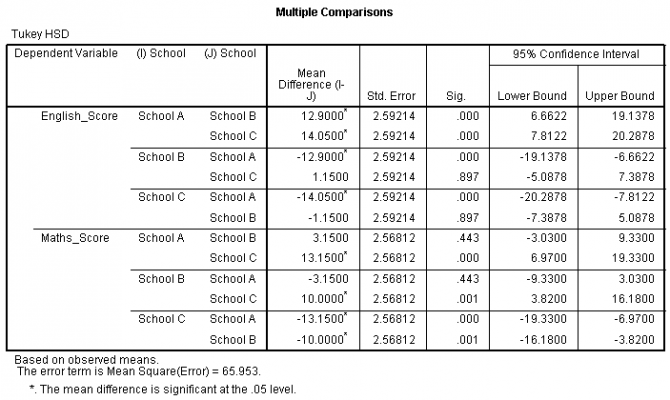
در این جدول نتیجه آزمون تعقیبی توکی ارائه شده است. این جدول نشان می‌دهد برای میانگین نمرات انگلیسی تفاوت معنی‌دار بین مدارس A و B (p < .0005)، مدارس A و C (p < .0005) وجود دارد، اما بین مدارس B و C تفاوت معنی‌دار وجود ندارد (p = .897). هم چنین، میانگین نمرات ریاضی دارای تفاوت معنی‌دار بین مدارس A و C (p < .0005) و مدارس B و C (p = .001) است، اما بین مدارس A و B دارای تفاوت معنی‌دار نیست (p = .443). این نتایج را می‌توان در نمودارهای زیر هم دید:

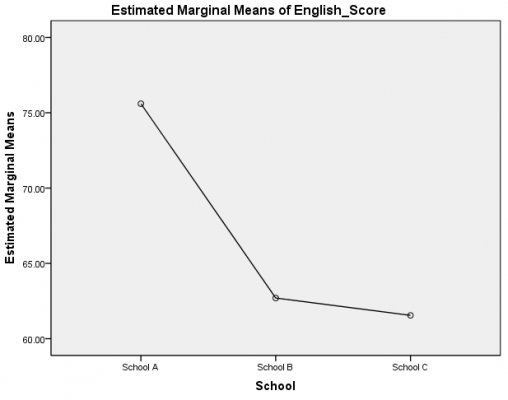
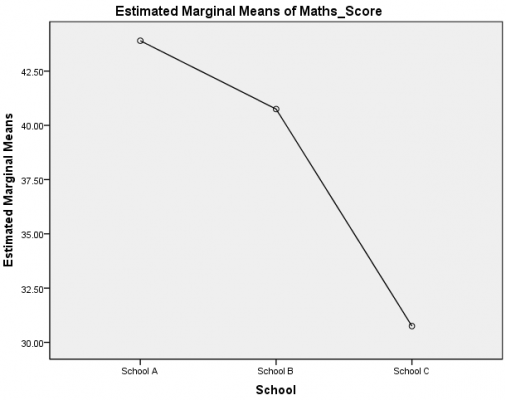
تحلیل واریانس چند متغره چه در مباحث تحلیل آماری پایان نامه، نوشتن فصل چهارم پایان نامه و چه در کسب و کار و سازمان های مختلف کاربرد های مختلفی دارد. در این مقاله سعی بر این بود تا شما با تمامی کاربرد های آن آشنا شوید. اما در این مسیر مشکلات فراوانی ممکن است که ایجاد شود. شما می توانید مشکلات را با افراد متخصص در میان بگذارید. این امکان در سایت آمار پیشرو در قسمت مشاوره آماری رایگان فراهم شده است. شما می توانید با تکمیل فرم منتظر تماس متخصصان باشید.

در این مقاله یکی از مباحث آماری آموزش داده شده است، برای با خبر شدن از جدید ترین آموزش ها و مطالب شما می توانید. صفحه اینستاگرامی شرکت آمار پیشرو را دنبال کنید.

در این مطلب سعی کردیم به بهترین شکل نحوه تحلیل واریانس چند متغیره را به شما آموزش دهیم اما قطعا این مبحث نیز همچون تمامی موضوعات دچار پیچیدگی های خاصی خواهد بود که چنانچه نیاز به انجام پروژه توسط افراد با تجربه باشد، شما می توانید در قسمت ثبت سفارش فرم مربوطه را تکمیل کرده و منتظر تماس متخصصان ما باشید. شرکت آمار پیشرو در سریعترین زمان ممکن با هزینه مناسب و با بهترین کیفیت این خدمات را در اختیار شما قرار خواهد داد.