همبستگی کانونی چیست?-تحلیل آن در SPSS

همبستگی کانونی به زبان ساده و با مثالی کاربردی و کاملا ملموس

همبستگی کانوني شبیه رگرسیون چند متغیری است، به این معنا که در این روش ترکیبی از متغیرهای پیش بینی کننده به منظور پیش بینی متغیر ملاک به کار برده می‌شود، تفاوت این دو روش در تعداد متغیرهای ملاک است. در رگرسیون چند متغیری فقط یک متغیر ملاک وجود دارد، در صورتی که همبستگی کانوني بیش از یک متغیر ملاک دارد.قبل از هز چیزی بهتر است که به مطلب رگرسیون سری بزنید و مفهوم آن را دریافت کنید.

فرض کنید محققی به نمره‌های یک عده دانشجو در متغیرهای پیش بینی کننده‌ای مانند خانواده، میانگین نمره های دبیرستان، علائق شغلی و تیپ شخصیت (درون‌گرایی و برون‌گرایی) دسترسی دارد. همچنین نمره های این دانشجویان در متغیرهای ملاکی مانند مدت فراغت از تحصیل، درآمد سالانه، پرسش‌های فیزیولوژیکی و روانی و میزان مشارکت در فعالیت‌های اجتماعی، که بعدا مورد اندازه‌گیری قرار گرفته‌اند، در دست است.

یک روش برای تعیین همبستگی بین متغیرهای پیش‌بینی کننده و متغیرهای ملاک این است که همبستگی هریک از متغیرهای پیش‌بینی کننده با هریک از متغیرهای ملاک به طور جداگانه با استفاده از روش همبستگی پیرسون محاسبه شود. روش دیگر، مطرح کردن این سؤال است که کدام دسته از متغیرهای پیش بینی کننده بهتر از دسته دیگر، متغیرهای ملاک را پیش بینی می‌کند. روشی که برای پاسخ دادن به این سؤال به کار برده می‌شود، همبستگی کانوني نامیده می‌شود.

همبستگی کانونی یکی از خدمات تحلیل آماری است که شما می توانید آن را خود انجام دهید یا به یک شرکت آماری بسپارید، اگر وقت لازم را دارید می توانید در این مطلب کامل یک مثال ملموس را حل کردیم که تمامی مواردی که به همبستگی کانونی مربوط می شود آموزش ببینید، اما چنانچه وقت کافی ندارید می توانید این نوع همبستگی را به عنوان یکی از خدمات تحلیل آماری با تعریف پروژه آماری از بخش خدمات سفارش دهید.

کاربرد همبستگی کانونی

تحقیقی که توسط هربرت والبرگ (۱۹۶۹) با استفاده از این روش اجرا شده است کاربرد آن ‌را نشان می‌دهد. هدف این تحقیق تعیین تاثیرات محیط اجتماعی کلاس، ویژگی‌های زندگی، شخصیتی و هوش دانش آموزان در یادگیری فیزیک در دبیرستان بود. تعداد زیادی متغیر در این تحقیق به کار برده شد: ۱۴متغیر برای اندازه‌گیری محیط اجتماعی کلاس، ۷ متغیر برای اندازه گیری شخصیت، ۲۰ سوال برای ویژگی‌های زندگی و ۶ نوع اندازه ‌گیری در مورد پیشرفت دانش آموزان در درس فیزیک (۳مورد، شناختی و ۳ مورد، غیر شناختی).

بدین طریق توده‌ای از اطلاعات به دست آمد که ابتدا با استفاده همبستگی ساده خطی پیرسون مورد تجزیه و تحلیل قرار گرفتند. یعنی، ابتدا همبستگی هر متغیر پیش بینی کننده با هریک از متغیرهایی که پیشرفت دانش آموزان را در درس  فیزیک نشان می‌داد، محاسبه شد. سپس همبستگی کانوني به منظور توصیف دقیق همبستگی‌ها محاسبه شد.

از این تجزیه و تحلیل، دو همبستگی کانوني معنادار به دست آمد (این همبستگی‌ها شبیه عواملی بودند که در تجزیه و تحلیل عاملی پیدا می‌شوند). بر اساس اولین همبستگی کانوني، کلاس‌هایی که بهترین ملاک شناختی یادگیری درس فیزیک را کسب کرده‌اند، کلاس‌هایی هستند که دانش آموزان آنها طرفدار استبداد و تمرکز قدرت در کلاس نیستند، بهره‌ی هوشی و نمره‌های درسی بالایی دارند و کلاس خود را مشکل می‌دانند.

بر اساس همبستگی دوم کانوني، کلاس‌هایی که بهترین ملاک غیر شناختی یادگیری درس فیزیک را کسب کرده‌اند، کلاس‌هایی هستند که دانش آموزان آنها جوایز بیشتری را در مسابقات علمی کسب کرده‌اند، مطالعات غیر درسی بیشتری دارند، مدرسه را دوست دارند و فکر نمی‌کنند که کلاسشان کسالت آور و نامطبوع است.

اساس ریاضی همبستگی کانوني

همانند محاسبات و تفسیر نتایج همبستگی کانونی کاملا پیچیده است. با وجود این، نوشته‌های مجله‌های علمی – تحقیقی حکایت از آن دارند که استفاده از این روش، روز به روز افزایش می‌یابد. همبستگی کانوني را می‌توان در پیش بینی‌های عملی به کار برد. این روش به ویژه زمانی به کار برده می‌شود که محقق علاقه‌مند است همبستگی بین دسته‌ای از متغیرهای پیش‌بینی کننده را با گروهی از متغیرهای ملاک اندازه‌گیری و کشف کند، و اندازه گیری‌های این دو دسته متغیر نیز ممکن است در زمان‌های مختلف انجام شده باشند.

تحلیل همبستگی کانوني شناخت وکمی کردن رابطه بین دو مجموعه از متغیرها را بررسی می‌کند. به عنوان مثال رابطه بین متغیرهای سیاست دولتی با متغیرهای هدف اقتصادی و یا رابطه متغیرهای عملکرد دانشکده با متغیرهای موفقیت آمیز پیش دانشگاهی را شامل می‌شود.

می‌خواهیم رابطه بین دو گروه از متغیرها را اندازه گیری کنیم، فرض کنید اولین گروه از p متغیر را با بردار تصادفی  X¹ و دومین گروه از q متغیر را با بردار تصادفی X² نشان دهیم.

برای بردارهای تصادفی X¹ و  X²داریم:

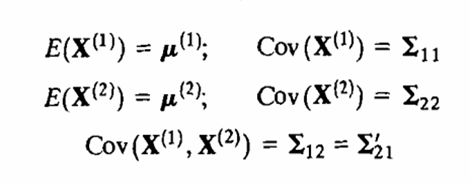
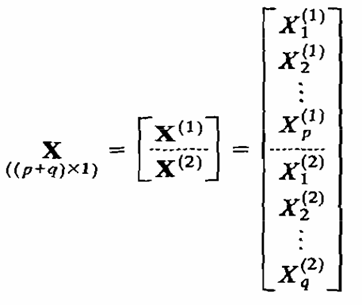
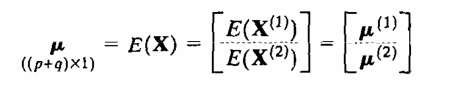
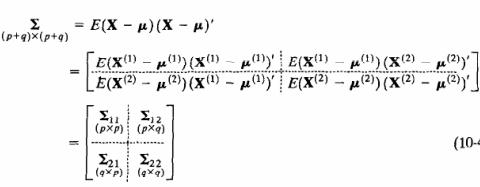
کوواریانس‌های بین زوج‌های متغیرها از مجموعه‌های مختلف، یک متغیر ازX¹ ، یک متغیر از X² در Σ₁₂ یا معادل با آن در Σ ₂₁ قرار دارد. یعنی pq عضو Σ₁₂ ارتباط بین دو مجموعه را اندازه می‌گیرد. وقتی p و q نسبتا بزرگ باشند، تعبیر اعضای Σ₁₂ بطور جمعی معمولا بی فایده است. علاوه بر این اغلب ترکیبات خطی متغیرها که اندازه‌های خلاصه شده ساده ای را از مجموعه ای از متغیرها فراهم می‌کنند، برای اهداف تخمینی و مقایسه ای جالب و مفیداند. کار اصلی تحلیل همبستگی کانونی این است که روابط بین مجموعه های X¹وX² را بجای pq کوواریانس در Σ₁₂ بر حسب چند کوواریانسی که به دقت انتخاب شده اند، خلاصه کند.

متغیرهای کانونی و همبستگی های کانوني

تحلیل همبستگی کانوني روی همبستگی بین یک ترکیب خطی از متغیرهای یک مجموعه و یک ترکیب خطی از متغیرهای مجموعه دیگر متمرکز می‌شود. ابتدا هدف ما این است که دو ترکیب خطی با بیشترین همبستگی را تعیین کنیم سپس دو ترکیب خطی را تعیین می‌کنیم که در میان تمام زوج های ناهمبسته با زوج انتخاب شده اول دارای بیشترین همبستگی باشد و این فرآیند را ادامه می‌دهیم. زوج های ترکیبات خطی را متغیرهای کانوني و همبستگی آن‌ها را همبستگی های کانوني می‌نامیم.

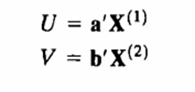
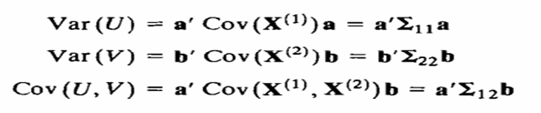
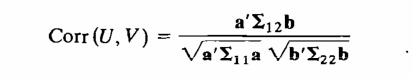
بردارهای ضرایب a و b را طوری پیدا می‌کنیم که همبستگی فوق تا حد ممکن بزرگ باشد.

تعریف:

اولین زوج متغیرهای کانوني، زوج ترکیب خطیU¹  وV¹است که دارای واریانس‌های واحد بوده که همبستگی فوق را ماکزیمم کند.

دومین زوج از متغیرهای کانوني، ترکیبات خطیU²  وV²هستند که دارای واریانس‌های واحد است که همبستگی فوق را در میان تمام انتخاب‌هایی که با اولین زوج متغیرهای کانوني ناهمبسته می‌باشد را ماکزیمم کند.

kامین زوج از متغیرهای کانوني، ترکیبات خطیU^k  وV^kهستند که دارای واریانس‌های واحد بوده که همبستگی فوق را در میان تمام انتخاب‌های ناهمبسته باk-1 زوج متغیر کانوني قبلی ماکزیمم کند. همبستگی بین زوج kام از متغیرهای کانوني را همبستگی کانوني kام می‌نامند.

بردارهای α^k  وb^k به ترتیب kامین بردارهای همبستگی کانوني برای X¹وX² نامیده می‌شوند.

تحلیل همبستگی کانوني دارای بعضی خاصیت های ماکسیمال مشابه با خاصیت های تحلیل مولفه اصلی است. اما در حالیکه تحلیل مولفه اصلی بستگی های درونی بین مجموعه ای از متغیرها را در نظر می‌گیرد، تمرکز همبستگی کانوني بر همبستگی بین دو گروه ازمتغیرهاست.

یک راه بررسی تحلیل همبستگی کانوني بسط رگرسیون چندگانه است. بخاطر آورید که درتحلیل رگرسیون چندگانه متغیرها به یک مجموعهx  شامل q متغیر و یک مجموعه y شامل p=1 متغیر افراز می‌شوند. جواب رگرسیون چندگانه مستلزم پیداکردن آن ترکیب خطی ′xα است که قویا با y همبسته است. حال آنکه در تحلیل همبستگی کانوني مجموعه y شامل بیشتر از یک متغیر است.

در جستجوی بردارهای a و b هستیم که همبستگی بین′X¹ α  و ′X² bرا ماکزیمم می‌کنند. اگرX¹  به عنوان علت X² تعبیر شود آنگاه ′X¹ α را ممکن است بهترین پیشگو′X² b و را ملاک بیشترین قابلیت  پیشگویی نامید.

پیش از انجام تحلیل همبستگی کانونی در SPSS بهتر است بدانید ابتدا نرم افزار spss چیست؟

نرم افزار SPSSبه عنوان یکی از پر کاربرد ترین نرم افزار های آماری شناخته می شود،دوره آموزش نرم افزار SPSS یک دوره کامل که با مثال های کاربردی تمامی مباحث کاربردی در نرم افزار را گام به گام آموزش میدهد،علاوه بر این از پشتیبانی خیلی خوبی برای انجام پروژه برخوردار است.یک فرصت اشتعال خوب نیز در پروژه های آماری برای مهارت آموزان فراهم خواهد شد.

تحلیل همبستگی کانونی در SPSS

برای اجرای فرمان همبستگی کانونی از مسیر Analyze → Correlate → Canonical Correlation استفاده می‌کنیم.

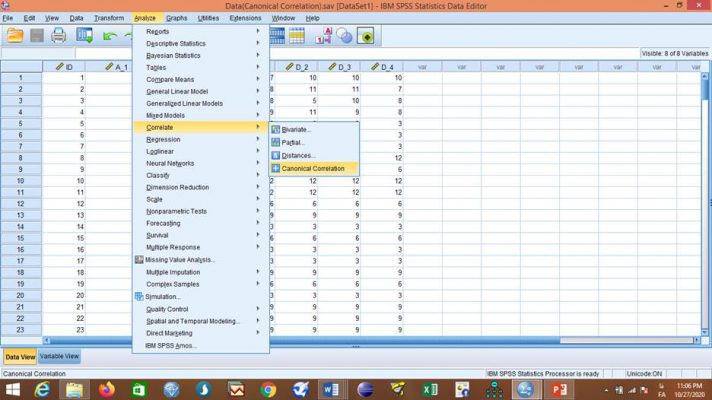
متغیرهای گروه اول را در Set1 و متغیرهای گروه دوم را در Set2 قرار می‌دهیم.

خروجی به شکل زیر نمایش می‌یابد:

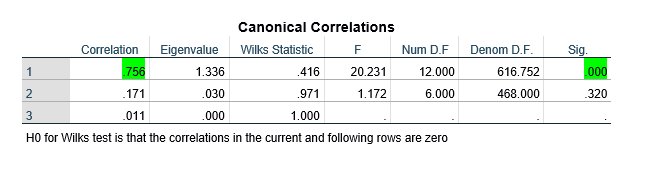
در کانون اول، ضریب همبستگی کانونی بین دو متغیر کانونی استرس شغلی و حمایت خودمختاری برابر 0/756 و مقدار معناداری متناظر با آن کوچکتر از 0/50 (0/000) به دست آمده است. بنابراین ضریب همبستگی کانونی بین این دو متغیر در سطح معناداری 0/50 معنادار است. مجذور ضریب همبستگی کانونی (0/756) ریشه کانونی نام دارد و برابر 0/571 است که یعنی متغیرهای اصلی مربوط به متغیر کانونی استرس شغلی 57 درصد از تغییرات متغیرهای اصلی مربوط به متغیر کانونی حمایت خودمختاری را پیش‌بینی و تبیین می‌کنند و بالعکس.

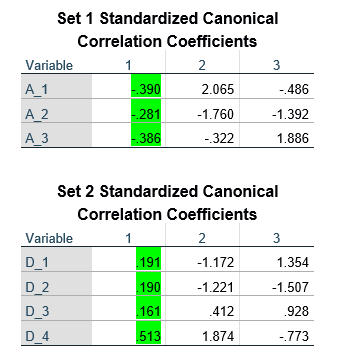
اعداد هایلایت شده در جدول زیر آمده است:

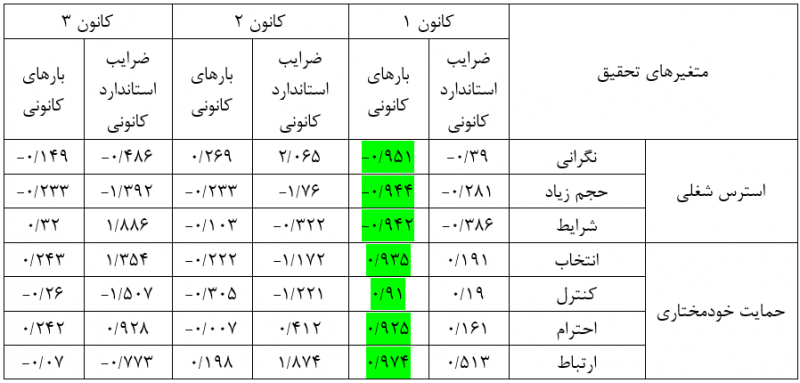
متغیرهای نگرانی، حجم زیاد و شرایط با بارهای کانونی 0/951-، 0/944- و 0/942- نقش معناداری را در پیش‌بینی متغیر کانونی حمایت خود مختاری داشته‌اند. و مجذور این بارهای کانونی به ترتیب 0/904، 0/891 و 0/887 است. در پیش بینی واریانس متغیر حمایت خودمختاری سهم متغیر نگرانی 90 درصد، سهم متغیر حجم زیاد 89 درصد و سهم متغیر شرایط 89 درصد است.

متغیرهای انتخاب، کنترل، احترام و ارتباط با بارهای کانونی 0/935، 0/91، 0/925 و 0/974 نقش معناداری را در پیش‌بینی متغیر کانونی استرس شغلی داشته‌اند. و مجذور این بارهای کانونی به ترتیب 0/874، 0/828، 0/856 و 0/949 است. در پیش بینی واریانس متغیر استرس شغلی سهم متغیر انتخاب 87 درصد، سهم متغیر کنترل 83 درصد، سهم متغیر احترام 86 درصد و سهم متغیر ارتباط 95 درصد است.

همبستگی کانونی یکی از انواع همبستیگ است که کاربرد های متنوعی دارد، در این مطلب سعی شده کلیه مطالب مربوط به همبستگی کانونی مطرح گردد اما چنانچه در مسیر اجرای آن به مشکل برخورد کردیدو نیاز به مشورت با افراد با تجربه را داشتید، در قسمت مشاوره آماری رایگان می توانید با متخصصان با تجربه آمار پیشرو ارتباط برقرار کنید. چنانچه علاقه مند به مباحث آماری هستید می توانید صفحه اینستاگرام آمار پیشرو را دنبال کنید و از مطالب جدیدی که بر روی سایت آپلود می گردد استفاده کنید.

همبستگی کانونی ممکن است در برخی پروژه ها از پیچیدگی خاصی برخوردار باشد، در این میان شما می توانید با ثبت سفارش در سایت آمار پیشرو از کارشناسان با تجربه در انجام همبستگی کانونی استفاده کنید.