آزمون Z در SPSS با مثال ملموس

آزمون Z یا آزمون خطای استاندارد میانگین یکی از مفاهیم مهم در علم آمار است. ما در این مطلب سعی کردیم به صورت ملموس ابتدا مفهوم آن را برای شما شرح دهیم و سپس آن را در SPSS اجرا کنیم. در ادامه همراه ما باشید. چنانچه می خواهید بیشتر و بهتر با تمامی قابلیت های نرم افزار SPSS آشنا شوید می توانید به دوره آموزشی SPSS مراجعه کنید.

آزمون z چیست؟

ازمون خطای استاندارد یک آزمون آماری است و در صورتیکه واریانس دو جامعه معلوم و حجم نمونه بزرگ باشد برای تعیین برابری میانگین دو جامعه به کار می رود.

فرض میشود که آماره آزمون داری توزیع نرمال می باشد و برای انجام دقیق آن باید پارامترهای مزاحم مانند انحراف معیار معلوم باشند.

نکات مهم درباره آزمون خطای استاندارد میانگین

Z-test  یک آزمون آماری است و وقتی واریانس معلوم و اندازه نمونه زیاد باشد، تفاوت یا عدم تفاوت میانگین دو جامعه را تعیین میکند.

آزمون z آزمون فرضیه ای است که در آن آماره z دارای توزیع نرمال میباشد.

آماره z یا نمره z عددی است که نتیجه آزمون z را نشان می دهد.

آزمون خطای استاندارد میانگین ارتباط نزدیکی با آزمون های t دارند، اما آزمون های t هنگامی به کار میروند که اندازه نمونه ها کوچک است. در آزمون های  z فرض می کنند که انحراف استاندارد معلوم است، در حالی که در آزمونt   انحراف استاندارد نامعلوم است.

نرم افزار SPSS چیست و چه کاربردی دارد؟

درک بهتر و ملموس آزمون زد

 آزمون z نیز یک آزمون فرضیه است که در آن آماره  z دارای توزیع نرمال است. از آزمون z بهتر است برای نمونه های بزرگتر از 30 استفاده شود زیرا تحت قضیه حد مرکزی، هرچه تعداد نمونه ها بیشتر شود، نمونه ها تقریبا از توزیع نرمال پیروی می کنند.

هنگام انجام آزمون z ، فرضیه صفر و فرضیه مخالف، آلفا و نمره z باید بیان شوند. در مرحله بعد، باید آماره آزمون محاسبه شود و نتایج بیان شود. آماری z یا نمره z عددی است که نمایانگر چند انحراف معیار بالای یا کمتر از میانگین جامعه است و در واقع یک نمره حاصل از آزمون z میباشد.

نمونه ای از آزمون هایی که می توانند به صورت آزمون های z انجام شوند شامل آزمون مکان یک نمونه ای، آزمون مکان دو نمونه ای، آزمون اختلاف زوج و برآورد حداکثر احتمال است. آزمونz  ارتباط نزدیکی با آزمونt  دارند، اما آزمون t  هنگامی به کار میرود که حجم نمونه کوچک باشد همچنین، در آزمونt  فرض می کنند که انحراف استاندارد نامعلوم است، در حالی که در آزمون  z  فرض می کنند که انحراف استاندارد مشخص است. اگر انحراف معیار جامعه نامعلوم باشد، فرض برابری واریانس نمونه با واریانس جامعه صورت می گیرد.

یک نمونه آزمون z تک نمونه ای

فرض کنید یک سرمایه گذار می خواهد آزمایش کند که آیا متوسط بازده روزانه سهام بیش از 1 درصد است، یک نمونه تصادفی ساده با حجم 50 انتخاب می کند و بازده این نمونه به طور متوسط 2 درصد است. فرض کنید انحراف معیار بازده 2.5 درصد باشد. بنابراین، فرضیه صفر این است که میانگین یا میانه  برابر با 3 درصد باشد.

فرض کنید الفا 0.05 انتخاب شده است در این صورت الفا در هر طرف آزمون 0.025 است. همچنین فرضیه آماری دو طرفه می باشد. متعاقبا اگر مقدار z بزرگتر از  1.96 یا کوچکتر از 1.96- باشد فرضیه صفر رد میشود. آماره z مقدار بحرانی 1.96 یا 1.96- را دارد. میانگین بازده انتخاب شده برای آزمون، از میانگین نمونه ها محاسبه میشود سپس مقدار حاصل را بر انحراف استاندارد تقسیم بر ریشه مربع تعداد مقادیر تقسیم شده تقسیم کنید. بنابراین آماره آزمون برابر است با:

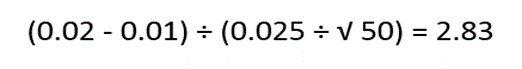
چون z بزرگتر از 1.96 است سرمایه گذار فرض صفر را رد می کند و نتیجه می گیرد که میانگین بازده روزانه بیشتر از 1 درصد است.

تفاوت بین آزمون Z و آزمون T چیست؟

Z-test  ارتباط نزدیکی با T-Test  دارند ، اما آزمون های t هنگامی به کار میروند که اندازه نمونه ها کوچک است. در آزمونهای z فرض می کنند که انحراف استاندارد معلوم  است، در حالی که در آزمونt   انحراف استاندارد نامعلوم است. اگر انحراف استاندارد جامعه ناشناخته باشد، اما اندازه نمونه بیشتر یا برابر با ۳۰ باشد، فرض واریانس نمونه برابر واریانس جامعه استفاده میکنیم و آزمون z را به کار میبریم.برای دریافت اطلاعات بیشتر درباره آزمون T می توانید به این مطلب مراجعه کنید.

قضیه حد مرکزی چیست؟

در مطالعه نظریه احتمال، نظریه حد مرکزی بیان میکند با فرض اینکه تمام نمونه ها دارای حجم یکسان هستند، و بدون در نظر گرفتن شکل توزیع جامعه، هر چه حجم نمونه بیشتر شود توزیع نمونه از توزیع نرمال پیروی میکند. لازم به ذکر است حجم نمونه های برابر یا بیشتر از 30 در قضیه حد مرکزی برای  پیش بینی ویژگی های جامعه کافی است.

آماره Z چیست ؟

 آماره  zیک عدد است که نشان میدهد چند انحراف استاندارد بالا یا پایین تر از میانگین جامعه است که نمره حاصل از یک آزمون صفر شود، نشان میدهد که مقدار نقطه   zاست یا اندازه گیری عددی رابطه یک مقدار را با میانگین مقادیر نشان میدهد.اگر مقدار z مورد نظر با میانگین مقادیر یکسان است.

مقادیر z ممکن است مثبت یا منفی باشند مقادیر مثبت نشان دهنده ی مقدار بالاتر از میانگین و مقادیر منفی نشان دهنده مقدار کمتر از میانگین است.

“z-test” یک اصطلاح عمومی برای هر آزمون آماری است که در آن آماره آزمون (معمولاً به عنوان آماره z شناخته می شود) از یک توزیع نرمال پیروی می کند. همان طور که با آزمون های t، انواع مختلفی از آزمون ها تحت دسته آزمون  tوجود دارد، به همین ترتیب انواع مختلفی از آزمون z وجود دارد.

با این حال، رایج ترین استفاده از اصطلاح “z-test” به آزمون  zتک نمونه ای اشاره دارد، در واقع این شایع ترین تنوع مورد استفاده آزمون z است. آزمون z تک نمونه ای به ما این امکان را می دهد که میانگین یک نمونه را با میانگین فرضی جامعه ای که نمونه از آن ها گرفته شده است مقایسه کنیم تا مشخص شود که آیا میانگین نمونه با میانگین فرضی تفاوت قابل توجهی دارد یا نه.

در این مثال ما،  آزمایش می کنیم که آیا کودکان مناطق محروم در یک سال معین وزن متوسط بیشتری نسبت به میانگین وزن تمام کودکان همان  سال دارند یاخیر. چون میانگین ها را مقایسه میکنید، داده هایی که شما استفاده می کنید باید داده های پیوسته یا scale (فاصله ای یا نسبتی) باشد. مثلا وزن، قد، وزن، شاخص توده بدنیBMI، دما، درامد و …

این مثالی از آزمون تک نمونه ای z است که مربوط به کودکانی است که در  سال 2016-2017 مورد تحقیق قرار گرفته اند. 34467 نفر پاسخ دهنده وجود دارد. دو متغیری که بررسی می کنیم:

• وزن – تمام کودکان همان سال به کیلوگرم (WeightAll)
• وزن محروم ترین کودکان همان سال (1 IMD)، به کیلوگرم (MostDep)

نکته: هر دو متغیر متغیر پیوسته یا  scaleهستند و بنابراین کد گذاری نمی شوند.

یکی از فرضیات آزمون تک نمونه ای  z این است که توزیع داده ها تقریباً نرمال است. برای تست نرمال بودن با استفاده از SPSS این گونه عمل میکنیم:

به منوی نوار ابزار میرویم:

در کادری که باز می شود، هر دو متغیر را به کادر “متغیرها” منتقل کنید و سپس OK را کلیک کنید تا تجزیه و تحلیل انجام شود. ابتدا باید تعیین کنید که داده ها از توزیع نرمال پیروی میکنند سپس می توانید اقدام به اجرای آزمون تک نمونه ای  zکنید.

پیش از انجام هر آزمون آماری در خور توجه است که بخش های امار توصیفی متغیر ها را بررسی نماییم. برای این کار به منوی نوار ابزار میرویم:

در کادری که باز می شود، هر دو متغیر را به کادر لیست متغیرها منتقل کنید.

گزینه  “Display frequency tables” را تیک بزنید. در سمت راست کادر، روی دکمه “Statistics” کلیک کنید. این کادر دیگری را باز می کند و شما پارامتر هایی که نیاز به سنجش ان ها دارید از قبیل، میانگین، میانه، انحراف استاندارد، واریانس، و دامنه را انتخاب می کنید. سپس روی ادامه کلیک کنید.

سپس به صفحه قبلی بازمیگردید. در سمت راست کادر، روی دکمه “نمودارها” کلیک کنید. این یک کادر دیگری را باز می کند، و گزینه “Histograms” انتخاب کنید .

در  SPSS یک تابع معین برای انجام آزمون تک نمونه ای z وجود ندارد .به همین دلیل میتوانید در صفحه syntax با استفاده از کد های زیر این آزمون را انجام دهید.

با استفاده از مسیر زیر صفحه syntax را باز کنید:

سپس کد های زیر را اجرا نمایید

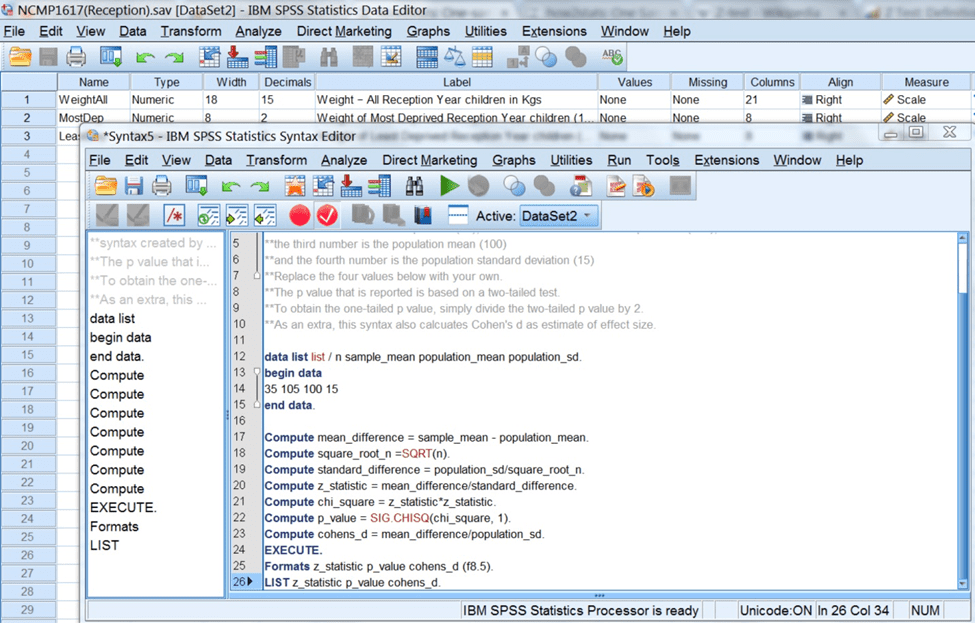
در کادر زرد رنگ مشخص شده در عکس زیرحجم نمونه، میانگین نمونه، میانگین جامعه و انحراف استاندارد است که باید مطابق با نمونه و جامعه آماری مد نظرتان تغییر کند اما بقیه دستورات یکسان میباشند.

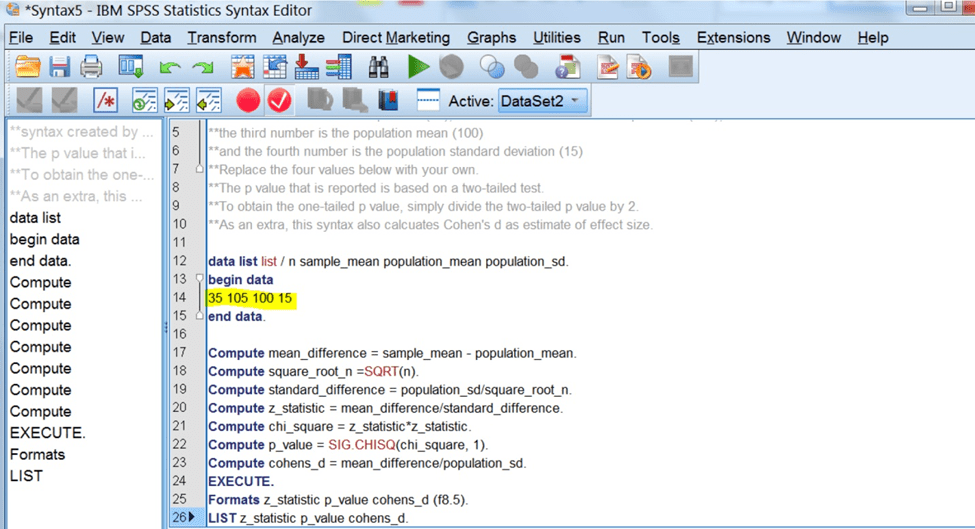
ما در کادر زیر پارامتر های ذکر شده را مطابق با مشخصات مثال تغییر دادیم:

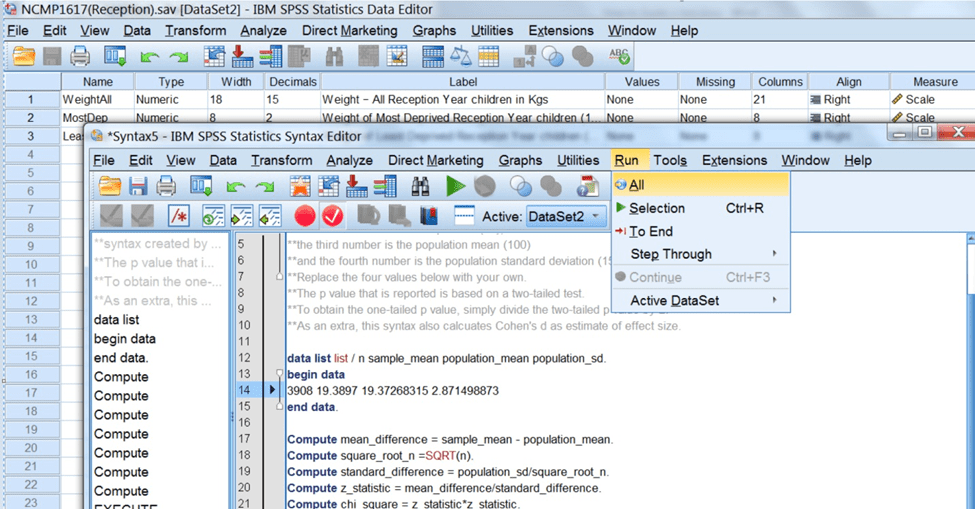
بعد از اینکه گزینه Run all را انتخاب میکنید خروجی زیر به نمایش می اید:

SPSS دو جدول به ما میدهد که اولین مربوط به شاخص های گرایش مرکزی میباشد. بر خلاف دامنه، میانگین دو گروه به طور چشمگیری تفاوت ندارد. جامعه کلی دامنه بزرگتری نسبت به جامعه  گروه محروم دارد. با توجه به توزیع، بیشتراکثریت وزن جامعه کلی بین 16.5 تا 22.24 کیلوگرم تغییرمی کند، در حالی که در گروه محروم، وزن اکثریت بین 16.31 تا 22.47 کیلوگرم تغییر می کند. به نظر می رسد تفاوت کوچکی وجود دارد، اما به نظر می رسد همپوشانی روشنی بین توزیع ها نیز وجود دارد.

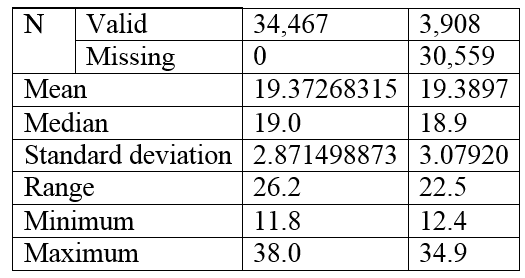
جدول دوم در خروجی SPSS:

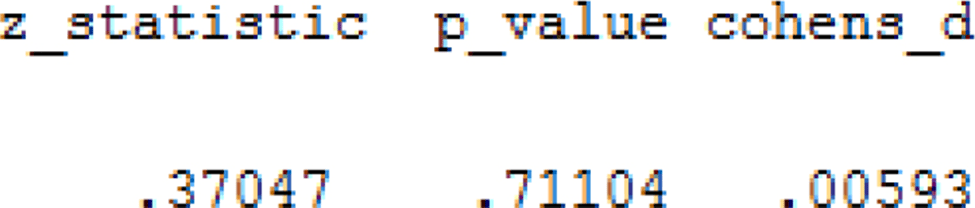
مشاهده میکنیم که آماره z برابر با 0.37047 و پی ولیو 0.71104 میباشد. نتایج ما معنی دار نیستند.      بنابراین فرضیه صفر رد نمیشود یعنی میانگین وزن کودکان محروم  بالاتر از میانگین وزن تمام کودکان نیست.

آزمون z دو نمونه ای

این آزمون بررسی میکند که در دو جامعه مستقل از هم رویدادی به طور مشابه رخ میدهد ؟

برای مثال آیا درصد مساوی از دانش آموزان دختر و پسر به برخی از سوالات امتحانی به درستی پاسخ می دهند؟ شکل زیر طرح هایی دارد که داده های مورد نیاز ممکن است چه شکلی باشد.

نمونه تصادفی ساده 175 نفر پسر و 164 نفر دختر 5 سؤال امتحانی را تکميل کردند. تعدادی از داده های خام در زیر نشان داده شده است

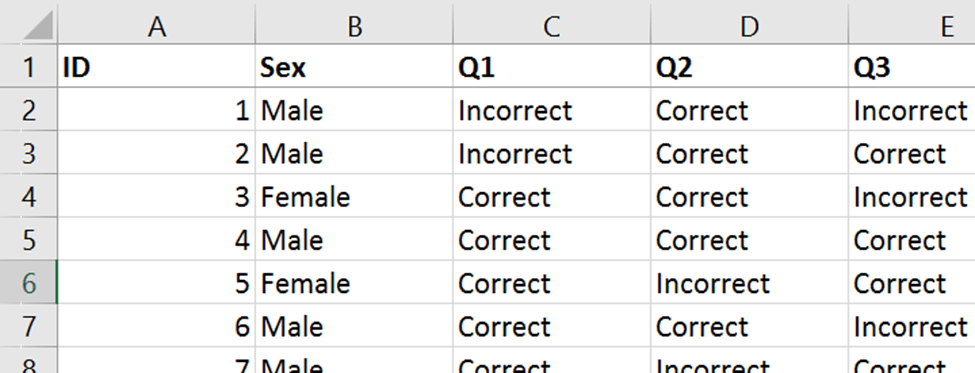
بیایید اول به سوال اول امتحان نگاه کنیم. داده های خام در مورد این سوال را می توان با جدول احتمالی نشان داده شده در زیر خلاصه کرد.

بنابراین جدول احتمالی ما درصد پاسخگویان زن و مرد را نشان می دهد که به درستی به سوال 1 پاسخ داده اند. اما در آمار معمولاً نسبت ها را بر درصدها ترجیح می دهیم. خلاصه یافته های ما، می بینیم که

• نسبت p1 = 0.720 از n1 = 175 دانش آموز پسربه این سوال درست پاسخ دادند
• نسبت p2 = 0.768 از n2 = 164 دانش آموز دختر به این سوال درست پاسخ دادند

در نمونه ما دانش آموزان دختر کمی بهتر از دانش آموزان پسر عمل کردند.

معمولا نتیج نمونه با جوامع خود متفاوت هستند.

حتی اگر کل جوامع مرد و زن به طور مشابه عمل کنند، باز هم ممکن است تفاوت نمونه کوچکی پیدا کنیم. این امر به راحتی می تواند ناشی ازانتخاب  نمونه های تصادفی دانش آموزان باشد. آزمون z تلاش می کند تا این فرضیه را باطل کند و به این ترتیب نشان دهد که جوامع واقعاً عملکرد متفاوتی انجام می دهند.

فرضیه صفر آزمون z برای نسبت های مستقل این است که تفاوت بین ۲ نسبت جامعه  صفر است.

اگر این فرض درست باشد، آنگاه تفاوت بین ۲ نسبت نمونه باید نزدیک به صفر باشد. نتایجی که با صفر بسیارفاصله دارند فرض صفر را رد میکنند .

فرضیات آزمون z

مشاهدات مستقل هستند

اندازه نمونه کافی باشد:

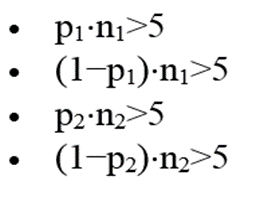
فرمول z

در قدم اول تفاوت بین دو نسبت نمونه را محاسبه میکنیم.

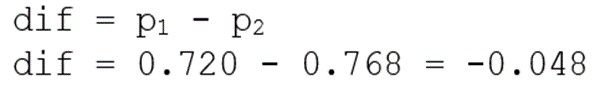
خطای استاندارد برای این تفاوت بستگی به نسبت جمعیت دارد. بدیهی است که ما آن را نمی دانیم اما ما می‌توانیم نسبت جمعیت را به طور  تخمینی محاسبه کنیم.

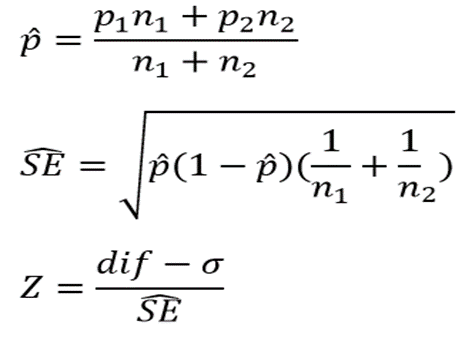
که δ تفاوت جامعه فرضی را نشان می دهد. فرضیه صفرما بیان می کند که δ = 0 (هر دو نسبت جوامع برابر است).

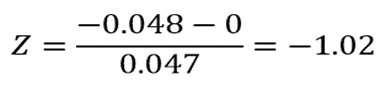
اگر فرضیات آزمون z برقرار باشند ، آنگاه z تقریباً از  توزیع نرمال استاندارد پیروی می کند.

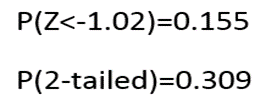
بنابراین فرض صفر رد نمیشود .

برای انجام آزمون z در SPSS گزینه خاصی وجود ندارد اما میتوانیم به جای ان از آزمون کای اسکوئر استفاده کنیم. مقدار حاصل از این آزمون معادل پی ولیو دو طرفه است که میتوانست از آزمون z به دست اید :

Analyze > Descriptive Statistics > Crosstabs

• متغیر های مستقل را در قسمت Rows  و متغیر های وابسته در قسمت columns  وارد کنید
• روی گزینه statistics  کلیک کنید سپس روی square روبه روی Chi-square  کلیک کنید
• سپس روی continue  و سپس ok  کلیک نمایید

امیدواریم در این مطلب توانسته باشیم تمام علامت سوال های ذهن شما را در زمینه آزمون Z پاسخ داده باشیم. شما می توانید مطالب جدید آماری را در صفحه اینستاگرام آمار پیشرو ببینید و آن را دنبال کنید. اگر سوالی دارید و نظرتون نسبت به این مطلب را می توانید در قسمت کامنت ها وارد کنید.