آزمون کولموگروف اسمیرنوف برای نرمال بودن داده ها در SPSS

آزمون کولموگروف اسمیرنوف چیست و چه کاربردی دارد؟

آزمون کولموگروف اسمیرنوف یکی از آزمون‌هایی که نام آن را برای بررسی نرمال بودن زیاد شنیده‌ایم. برای استفاده از بسیاری از روش‌های آماری معروف، لازم است داده‌ها از توزیع نرمال پیروی کنند. در حقیقت برای بسیاری از آزمون‌های پارامتری باید داده‌ها دارای توزیع نرمال باشند. به همین علت، لازم است پیش از استفاده از این آزمون‌ها، با بهره‌گیری از روش‌های آماری، درباره نرمال بودن داده‌های مورد بررسی اطمینان حاصل کنیم.

. بنابراین کاربرد آزمون کولموگروف اسمیرنوف در تعیین نرمال بودن داده‌ها به عنوان مثال در تحلیل آماری است.این آزمون به عنوان یکی از خدمات آماری شناخته می شود. که می توانید آن را انجام دهید و یا به افراد متخصص بسپارید. اما این آزمون، تنها روش برای بررسی نرمال بودن نیست و روش‌های گوناگون دیگری نیز برای این منظور وجود دارند.

انواع روش های نرمال بودن داده

در این مطلب، روش‌های بررسی نرمال بودن داده‌ها را شرح خواهیم داد. این روش‌ها دارای دو نوع کلی هستند . برخی از آن‌ها بر مبنای آزمون‌های آماری و برخی دیگر بر مبنای بررسی‌های بصری هستند. آزمون‌های آماری دارای این مزیت هستند که قضاوت عینی درباره نرمال بودن را فراهم می‌کنند، اما نقص آن‌ها این است که به اندازه کافی در حجم نمونه کوچک حساس نیستند و در حجم نمونه بزرگ نیز بیش از حد حساس هستند. به همین علت، برخی از آماردان‌ها ترجیح می‌دهند از نمودارها استفاده کنند که توسط آن‌ها می‌توان قضاوت ذهنی درباره نرمال بودن انجام داد.

مزیت تفسیرهای نموداری این است که در مواقعی که آزمون‌های عددی کم‌تر یا بیش‌تر از حد حساس هستند، امکان قضاوت خوب را به ما می‌دهند. با این حال روش‌های نموداری، بی‌طرف نیستند که نقص آن‌ها به شمار می‌رود. اگر از تجربه کافی برای تفسیر نمودارهای مربوط به بررسی نرمال بودن داده‌ها برخوردار نباشیم، بهتر است به نتایج عددی اتکا کنیم.

در ادامه، رایج‌ترین روش‌های بررسی نرمال بودن داده‌ها در نرم‌افزار SPSS را خواهیم دید و به ویژه بر اجرای آزمون کولموگروف اسمیرنوف در SPSS تمرکز خواهیم داشت. نرم افزار spss به عنوان یکی از پر کاربرد ترین نرم افزار های آماری شناخته می شود،دوره آموزش نرم افزار SPSS یک دوره کامل که با مثال های کاربردی تمامی مباحث کاربردی در نرم افزار را گام به گام آموزش میدهد، علاوه بر اینکه از پشتیبانی خیلی خوبی برای انجام پروژه برخوردار است.یک فرصت اشتعال خوب نیز در پروژه های آماری برای مهارت آموزان فراهم خواهد شد

SPSS چیست؟ به زبان ساده

آزمون کولموگروف اسمیرنوف در spss

فرض کنید مجموعه داده‌هایی شامل دو متغیر داریم. یکی از این متغیرها سطح آموزش نرم‌افزار (Course) در سه سطح مبتدی، متوسط و پیشرفته، و دیگری زمان صرف‌شده برای حل مسئله با نرم‌افزار (Time) است. داده‌ها شامل 30 آزمودنی است (حجم نمونه برابر با 30 است).  در این مجموعه داده‌ها، قصد داریم نرمال بودن متغیر زمان (Time) را با استفاده از SPSS بررسی کنیم. برای این کار، مراحل زیر را طی می‌کنیم:

مرحله 1

ابتدا از مسیر زیر، پنجره Explore را باز می‌کنیم:

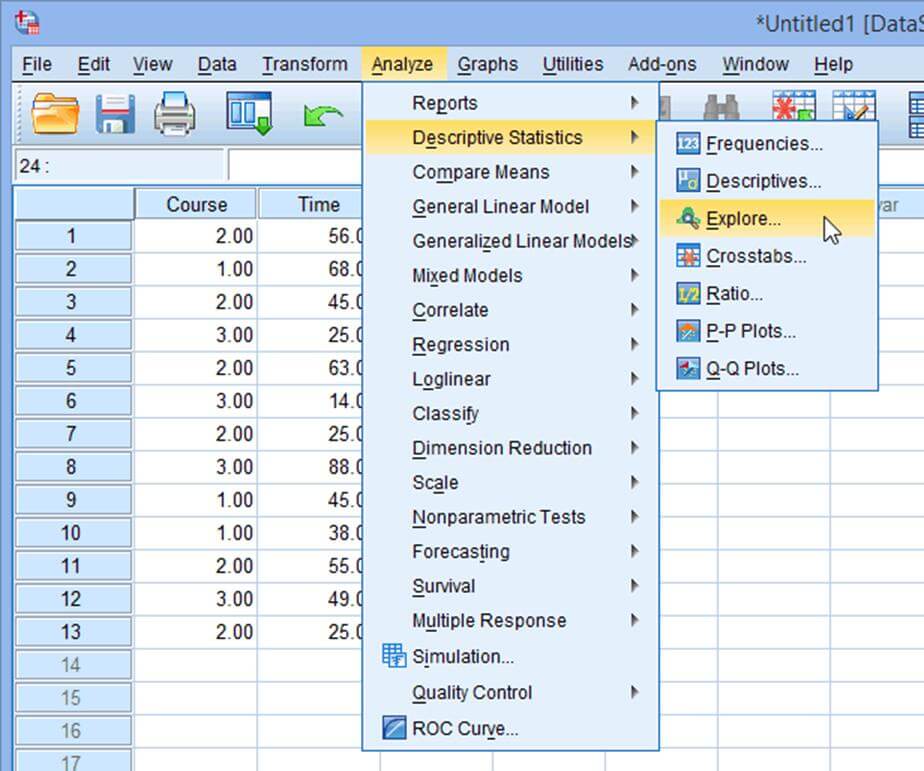
مرحله 2

پنجره Explore به صورت شکل زیر ظاهر می‌شود:

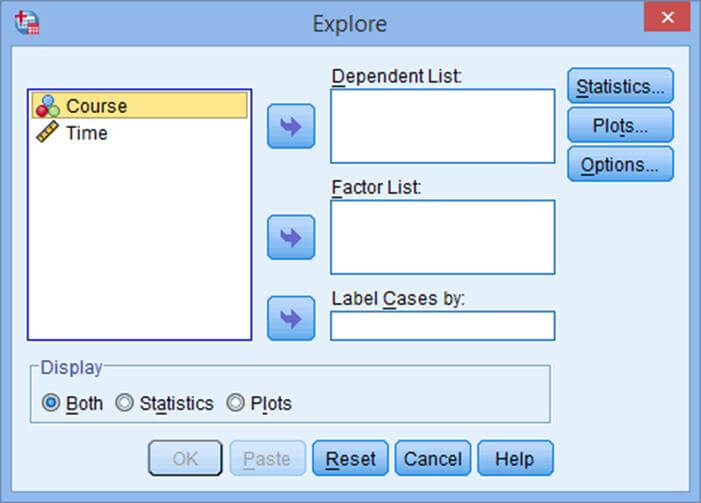
مرحله 3

متغیر زمان را که به دنبال بررسی نرمال بودن آن هستیم، همانند شکل زیر به قسمت فهرست متغیرهای وابسته منتقل می‌کنیم:

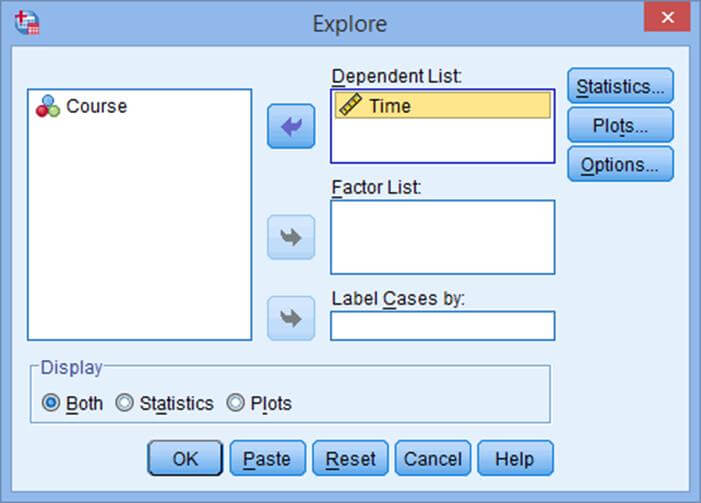
مرحله 4

حال روی دکمه آماره‌ها (Statistics) کلیک می‌کنیم تا پنجره آماره‌ها همانند شکل زیر ظاهر شود:

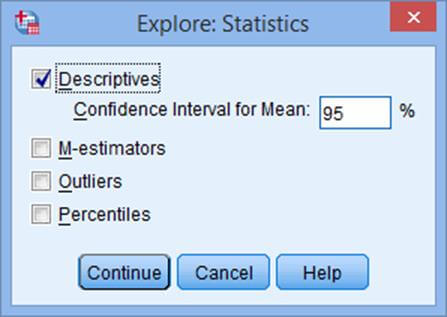
پس از آن کلید ادامه (Continue) را می‌زنیم.

مرحله 5

حال روی دکمه Plots کلیک می‌کنیم. در پنجره‌ای که ظاهر می‌شود،‌ گزینه‌ها را همانند شکل زیر انتخاب می‌کنیم:

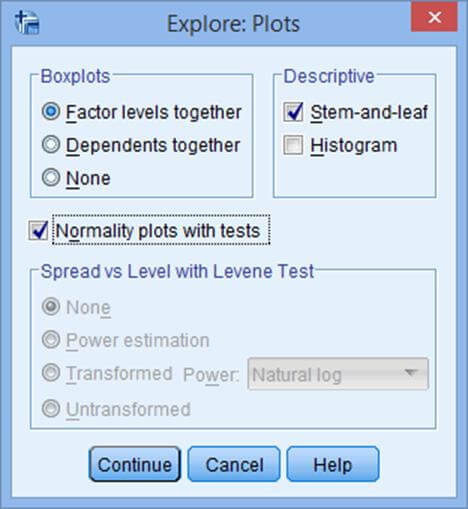
مرحله 6

روی کلید ادامه (Continue) کلیک می‌کنیم.

مرحله 7

روی کلید Ok کلیک می‌کنیم.

خروجی SPSS در بررسی نرمال بودن داده‌ها

وقتی در SPSS از پنجره Explore استفاده می‌کنیم، در خروجی آن تعداد زیادی جدول و نمودار ظاهر می‌شود. دلیلش آن است که از این پنجره فقط برای بررسی نرمال بودن استفاده نمی‌شود و کاربردهای دیگری نیز دارد. اما وقتی به دنبال بررسی نرمال بودن داده‌ها هستیم، معمولاً بر روی دو تا از این خروجی‌ها تمرکز می‌کنیم: جدول آزمون‌های نرمال که مربوط به روش‌های عددی بررسی نرمال بودن است، و نمودار چندک-چندک (Q-Q) نرمال که مربوط به روش‌های نموداری می‌شود.

آزمون کولموگروف اسمیرنوف برای بررسی نرمال بودن

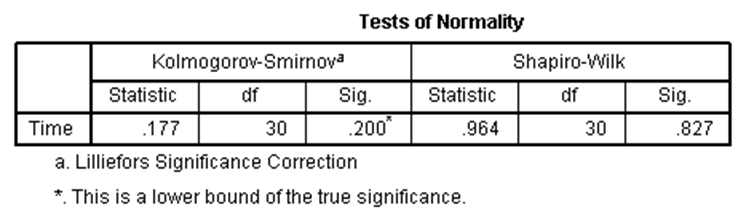
در جدول بالا، نتایج مربوط به دو آزمون آماری معروف برای نرمال بودن، یعنی کولموگروف اسميرنف و شاپیرو ویلک نشان داده شده است.

نکته: ممکن است بپرسید آیا دو آزمون کولموگروف اسميرنف و شاپیرو ویلک با هم تفاوتی دارند و از کدام یک از آن‌ها باید برای بررسی نرمال بودن داده‌ها استفاد کرد. آزمون شاپیرو ویلک فقط برای بررسی نرمال بودن داده‌ها استفاده می‌شود و دارای توان آماری بیش‌تری است. در حالی که آزمون کولموگروف اسميرنف را می‌توان برای بررسی تعلق داده‌ها به سایر توزیع‌های آماری نیز استفاده کرد. این آزمون دارای توان آماری کم‌تری نسبت به آزمون شاپیرو ویلک است و به داده‌های پرت نیز حساس است. بعضی آماردانان، آزمون شاپیرو ویلک را آزمون بهتری برای بررسی نرمال بودن داده‌ها می‌دانند، با این حال استفاده از آزمون کولموگروف اسميرنف رایج‌تر است.

حال چگونه از نتیجه آزمون‌های کولموگروف اسميرنف و شاپیرو ویلک، نرمال بودن را تشخیص بدهیم؟ اگر مقدار Sig در جدول این آزمون‌ها بزرگ‌تر از 0.05 باشد، آن‌گاه داده‌ها نرمال هستند و در صورتی که از 0.05 کوچک‌تر باشد، توزیع داده‌ها نرمال نیست. با توجه به جدول بالا می‌بینیم که برای آزمون کولموگروف اسميرنف، مقدار Sig برابر با 0.200 شده که چون از 0.05 بزرگ‌تر است، لذا نشان‌دهنده نرمال بودن داده‌ها است. این نتیجه برای آزمون شاپیرو ویلک نیز برقرار است، زیرا مقدار Sig آن برابر با 0.827 و بزرگ‌تر از 0.05 است.

نمودار Q-Q برای بررسی نرمال بودن

برای بررسی نرمال بودن داده‌ها از روی نمودار، می‌توانیم از خروجی مربوط به نمودار Q-Q استفاده کنیم. نمودار Q-Q مربوط به این مثال در شکل زیر آمده است. اگر داده‌ها به طور نرمال توزیع شده باشند، نقاط داده‌ها نزدیک به خط اریب قرار می‌گیرند. چنان چه نقاط داده‌ها از خط اریب فاصله داشته باشند و الگوی آن‌ها شبیه به این خط نباشد، آن گاه دارای توزیع نرمال نیستند.

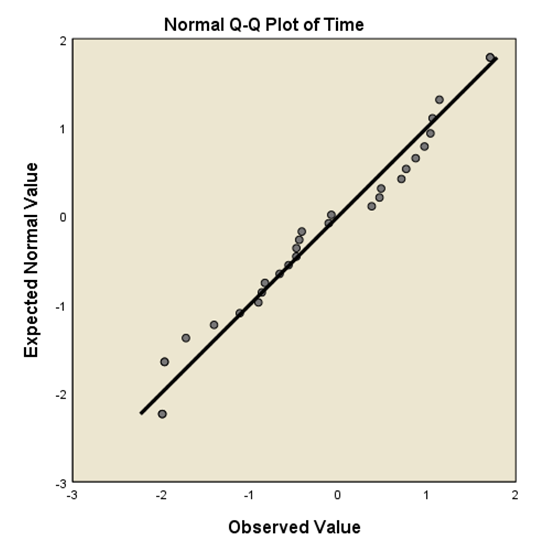
همان طور که در نمودار Q-Q در شکل بالا می‌توانیم ببینیم، نقاط داده‌ها بسیار نزدیک به خط اریب هستند و به نظر نمی‌رسد الگوی آن‌ها چندان تفاوتی با این خط داشته باشد. لذا با توجه به این نمودار، داده‌ها دارای توزیع نرمال هستند.

در این مقاله سعی کردیم یکی از رایج ترین روش های آزمون نرمال بودن نمودار یعنی آزمون کولموگروف اسمیرنوف به شما توضیح دهیم. چنانچه مشکلی در میانه راه دارید می توانید از افراد متخصص مشورت بگیرید، سایت آمار پیشرو در صفحه مشاوره آماری رایگان امکانی را فراهم کرده تا بتوانید با افراد متخصص ارتباط برقرار کنید و مشکلات پروژه را با آن ها مطرح کنید.

برای آگاهی از روش های دیگر نرمال بودن و بسیاری دیگر از مباحث آماری می توانید صفحه اینستاگرام آمار پیشرو را دنبال کنید. اگر می خواهید پروژه خود را به افراد خبره بسپارید و در کمترین زمان و با منصفانه ترین هزینه آن ها را تحویل بگیرید. به صفحه ثبت سفارش مراجعه کرده و با تکمیل فرم د راولین فرصت کارشناسان ما با شما تماس خواهند گرفت.