محاسبه آنلاین فرمول کوکران برای تعیین حجم نمونه

یکی از فرمول های پر کاربرد تعیین حجم نمونه فرمول کوکران است. محاسبه آنلاین فرمول کوکران تنها با وارد کردن حجم جامعه. در بسیاری از تحقیقات قرار است یک فرضیه را درباره‌ی یک جامعه‌ی خاص بررسی کنیم‌. مثلاً می‌خواهیم بدانیم آیا میانگین وزن دانش‌آموزان پسر سال سوم دبستان در ایران با متوسط جهانی آن برابر است یا خیر. طبق آمار اعلام‌شده، تعداد این دانش‌آموزان در ایران حدود ۶۵۰ تا ۷۰۰ هزار نفر است.این تعداد (حجم جامعه) حقیقتاً عدد بزرگی است و ناگفته پیداست که مراجعه به تک‌تک این دانش‌آموزان و ثبت میزان وزن آنان، کاری اگر نه غیرممکن ولی بسیار مشکل، وقت‌گیر و هزینه‌بر است.برای راحت تر شدن کار از فرمول کوکران استفاده می کنیم و حجم نمونه را به دست می آوریم. در ادبیات آماری، مراجعه به تک‌تک اعضای جامعه‌ی مورد بررسی «سرشماری» نامیده می‌شود.

محاسبه آنلاین تعیین حجم نمونه با فرمول کوکران

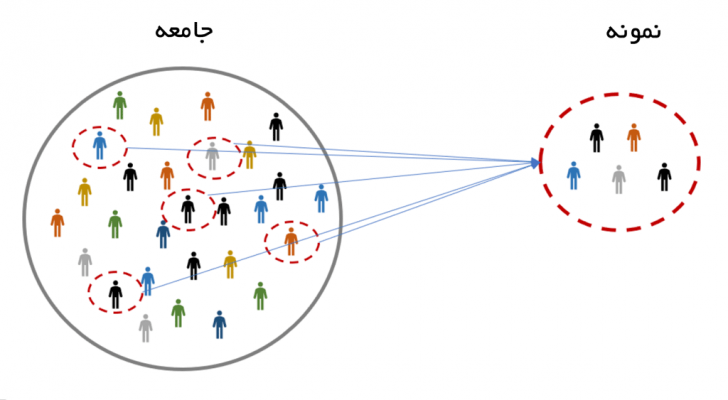
حجم نمونه یا سر شماری؟

معمولاً انجام سرشماری تنها از عهده‌ی سازمان‌های بزرگ و عمدتاً دولتی برمی‌آید. اما در مورد تیم‌های پژوهشی کوچک و به‌ویژه دانشجویان چه‌طور؟ پژوهش‌های آن‌ها از طریق مراجعه به اعضای جامعه‌ی مورد نظر باید انجام شود. اما این جامعه به لحاظ جمعیت آن قدر بزرگ یا به لحاظ دسترسی آن قدر پراکنده است که امکان مراجعه به همه‌ی اعضای آن وجود ندارد.

 این افراد چگونه می‌توانند پژوهش خود را به انجام برسانند؟ این جاست که آمار استنباطی می‌تواند به کمک پژوهش‌گران بیاید. آمار استنباطی به ما می‌گوید که نیاز نیست به سراغ همگی افراد جامعه برویم و می‌توانیم پژوهش خود را فقط با درصد نسبتاً کمی از جامعه انجام بدهیم، در حالی که نتایج به دست‌آمده هم‌چنان معتبر و علمی باشد.

 اما چگونه چنین امری ممکن است؟ عقل سلیم می‌گوید اگر بر اساس اطلاعات یک بخش از جامعه در مورد کل آن نتیجه‌گیری کنیم، این نتیجه‌گیری احتمالاً دچار اشتباه و خطاست. آمار استنباطی هم این حقیقت را تأیید می‌کند، اما دستاوردی که در اختیار ما قرار می‌دهد آن است که خطای نتیجه‌گیری را از یک مقدار مبهم و کنترل‌نشده به یک مقدار روشن و مهارشده تبدیل می‌کند.

در واقع آمار استنباطی شاخه‌ای از علم آمار است که با بهره‌گیری از قوانین متقَن ریاضی، مجوز علمی برای تعمیم نتایج به دست‌آمده از نمونه یک جامعه به کل جامعه را فراهم می‌کند.

آمار استنباطی می‌گوید ابتدا از جامعه‌ی خود نمونه‌ای را اختیار کنید و سپس سوالات یا فرضیات خود را با استفاده از آن بررسی و نتیجه‌گیری کنید. در نهایت این نتایج را به جامعه تعمیم دهید ولی بدانید که این نتیجه‌گیری را با در نظر گرفتن یک درصد مشخص و البته کوچکی خطا انجام داده‌اید. این خطا چون با روش‌های دقیق و منطقی لحاظ شده، نتایج ما را علمی و قابل پذیرش می‌کند.

حجم نمونه چیست؟

حال که دانستیم آمار استنباطی چه ابزار ارزشمندی را در اختیار ما قرار می‌دهد این را نیز باید بدانیم که استفاده از این ابزار اگر با رعایت شرایط آن همراه نباشد نتایج نادرست و گمراه‌کننده به دست خواهد داد. به عبارت دیگر، یک پژوهش‌گر برای آن که بتواند نتایج نمونه را به جامعه تعمیم دهد به دنبال مجوز علمی است و آمار استنباطی این مجوز را در اختیار وی قرار می‌دهد، ولی این مجوز همراه با اما و اگرهایی است. یکی از این اما و اگرهای بزرگ، حجم نمونه است.

حجم نمونه، تعداد اعضایی از جامعه است که در نمونه حضور پیدا می‌کنند. این تعداد چه قدر باید باشد؟شاید ساده‌ترین و رایج‌ترین پاسخ به این سوال بدین صورت باشد: هر چه حجم نمونه بیش‌تر باشد بهتر است! خبر تکان‌دهنده این است که طبق قوانین آمار استنباطی، این باور عمومی اشتباه است!!! ازدیاد نامتناسب حجم نمونه، تنها باعث افزایش نامتناسب دقت می‌شود اما کیفیت نتایج نهایی را افزایش نمی‌دهد.

چرا باید حجم نمونه را مشخص کنیم

برای توضیح این موضوع در مثالی که پیشتر ذکر شد، فرضیه‌ی برابری میانگین وزن دانش‌آموزان پسر سوم دبستان با مقدار 29 کیلوگرم را در نظر بگیرید (فرضیه صفر). دراین صورت فرضیه مقابل (فرضیه یک) به صورت عدم برابری میانگین وزن با 29 است.

برای این که فرضیه‌ صفر را رد کنیم، باید شواهد کافی ارائه کنیم که نشان دهند میانگین وزن، عددی غیر از 29 است. این شواهد از طریق داده‌های موجود در نمونه فراهم می‌شود. بدین صورت که با استفاده از اطلاعات موجود در داده‌ها و به کارگیری روش‌های آماری مناسب، در نهایت تصمیم می‌گیریم که باید فرضیه صفر را رد کنیم یا خیر.

 رد فرضیه صفر معادل با پذیرش فرضیه یک است و پذیرش آن نیز معادل با رد فرضیه یک قلمداد می‌شود. اما این تصمیم می‌تواند در واقعیت درست یا غلط باشد. به عبارت دیگر، ممکن است میانگین وزن دانش‌‌آموزان در واقعیت 29 کیلوگرم باشد، اما آن را به اشتباه نابرابر با 29 تشخیص بدهیم و در نهایت، فرضیه صفر را رد کنیم.

نتایج نمونه و خطا های آن

 در این صورت طبق تعاریف آماری، دچار خطای نوع یک شده‌ایم. در حالت دیگر، ممکن است مرتکب یک نوع دیگر از خطا بشویم که آن را خطای نوع دو می‌نامیم. این نوع خطا زمانی رخ می‌دهد که فرضیه یک را به اشتباه رد کنیم.

زمانی که تصمیم نهایی در مورد قبول یا رد فرضیات بر اساس نتایج نمونه را می‌گیریم، نمی‌دانیم که تصمیم اتخاذ‌شده در حقیقت درست است یا غلط. زیرا درست یا غلط بودن آن بستگی به مشخصات جامعه دارد و ما نیز از اطلاعات کل جامعه آگاهی نداریم. اطلاعات ما فقط محدود به نمونه است و به همین علت به استفاده از روش‌های آمار استنباطی روی آورده‌ایم.

 اما با وجودی که در واقعیت نمی‌دانیم در تصمیم اتخاذ‌شده دچار خطا شده‌ایم، می‌توانیم «احتمال» ارتکاب آن را در نظر بگیریم و آن را تا حد ممکن کاهش دهیم. به عبارت دیگر، در حالی که این امکان را نداریم که بدانیم تصمیم ما دچار خطا هست یا نه، می‌توانیم سعی کنیم طوری عمل تصمیم‌گیری را انجام دهیم که احتمال بروز خطا در آن بسیار کم باشد.

در این صورت، می‌توانیم با اطمینان بسیار بالایی نتایج تصمیم اتخاذشده را بیان و از آن در پژوهش‌های علمی استفاده کنیم. به طور دقیق‌تر اگر مقدار احتمال خطای نوع یک را با آلفا (alpha) و مقدار احتمال خطای نوع دو را با بِتا (beta) نشان دهیم، باید سعی کنیم کلیه‌ی عملیات مربوط به محاسبات آماری را طوری انجام دهیم که آلفا و بتا تا حد ممکن کوچک باشند.

اما مقادیر مناسب و معقول برای آلفا و بتا را چگونه انتخاب کنیم؟

حالت مطلوب این است که هر دوی آن‌ها با هم و تا حد امکان کوچک شوند، اما این کار در عمل غیرممکن است و می‌توانیم یکی را ثابت نگه داریم و دیگری را کوچک کنیم. در پژوهش‌ها، فرضیه صفر از اهمیت بیشتری برخوردار است، بدین معنا که اگر آن را به اشتباه رد کنیم (یعنی دچار خطای نوع یک شویم)، زیان ناشی از آن بیشتر از رد اشتباه فرضیه یک است (خطای نوع دو).

 لذا در انجام آزمون فرضیه‌ها، آلفا برابر با یک مقدار ثابت و کوچک (معمولاً 0.001، 0.05 یا 0.1) در نظر گرفته و سعی می‌شود بتا تا حد ممکن کوچک شود. البته در ادبیات آماری، معمولاً به جای بتا از توان آماری (statistical power) استفاده می‌شود. توان برابر است با یک منهای بتا، و لذا رابطه‌ی معکوس با بتا دارد. بنابراین در طراحی آزمون فرضیه، آلفا ثابت در نظر گرفته و مقدار توان تا حد ممکن بزرگ می‌شود.

تعیین حجم نمونه چه اهمیتی دارد؟

حال می خواهیم به تبیین حجم نمونه بپردازیم. همان طور که پیشتر گفتیم، کم‌تر بودن یا بیشتر بودن حجم نمونه از حد مورد لزوم، هر دو مشکلات خاص خود را به دنبال دارند. اگر حجم نمونه کم‌تر از حد لازم باشد، آن گاه آزمون مربوطه از توان و دقت کافی برای کشف حقیقت برخوردار نیست.

در مثال وزن دانش‌آموزان، ممکن است میانگین واقعی وزن دانش‌آموزان پسر در ایران 34 کیلوگرم باشد که در این صورت فرضیه صفر درست نیست. اما اگر نمونه با حجمی کم‌تر از مقدار مورد نیاز گردآوری شود، ممکن است آزمون نتواند اختلاف بین مقدار واقعی (34) با مقدار فرضیه‌ای (29) را تشخیص دهد و لذا فرضیه یک به اشتباه رد شود.

 در این حالت، حجم نمونه کم باعث کاهش بیش از حد توان آزمون و در نتیجه کاهش دقت آن شده است. اما از طرف دیگر، اگر حجم نمونه بیش از حد بزرگ انتخاب شود، توان آزمون و در نتیجه، دقت آن بیش از حد افزایش می‌یابد. این یعنی آزمون به اختلافات حتی کوچکِ شناسایی‌شده از نمونه با مقادیر فرضیه‌ای نیز حساس می‌شود.

در مثال مورد بحث، ممکن است میانگین واقعی وزن برابر با 28.5 باشد که در این صورت تقریباً می‌توان گفت فرضیه صفر درست است. اما اگر حجم نمونه بسیار بالا در نظر گرفته شود، آزمون ممکن است در نهایت از اطلاعات نمونه این اختلاف جزئی را معنی‌دار تشخیص دهد و به اشتباه فرضیه صفر را رد کند. در این حالت توان آزمون (و در نتیجه دقت آن) به نسبت آلفا بیش از حد بزرگ است که باعث می‌شود باز هم نتایج غیرواقعی برای آزمون به دست بیاید. بنابراین همان طور که می‌بینید در هر دو حالت، کوچک یا بزرگ بودن بیش از حد حجم نمونه، نتایج نامطلوبی ممکن است به بار بیاورد. 

حجم نمونه را چگونه تعیین کنیم؟

تا این جا دانستیم که حجم نمونه را نباید بر اساس باورهای نادرست تعیین کرد، چرا که ممکن است نتایج نامطلوبی به دست بدهد. پس چگونه باید حجم نمونه را تعیین نمود؟ پاسخ این است که حجم نمونه را باید با توجه به شرایط عمومی و شرایط اختصاصی هر مسئله تعیین کرد. منظور از شرایط عمومی، شرایطی هستند که در هر مسئله‌ی آزمون فرضیه جدا از نوع و هدف آن وجود دارند.

 به عنوان مثال، مقادیر آلفا و توان که در این بحث توضیح داده شدند، در هر مسئله آزمون فرضیه وجود دارند و لذا در تعیین حجم نمونه باید در در نظر گرفته شوند. اما شرایط اختصاصی، شرایطی هستند که بستگی به نوع مسئله دارند و در آزمون فرضیه‌‌ی مربوط به آن ظاهر می‌شوند.

مثلاً در مطالعات همبستگی که در آن‌ها از ضریب همبستگی پیرسون (Pearson) استفاده می‌شود، مهم است که بدانیم اندازه‌اثر (که در مطالب آینده توضیح داده خواهد شد) چه قدر باید باشد. لذا میزان اندازه‌اثر در نظر گرفته شده نیز در حجم نمونه تأثیر خواهد داشت.

تعیین حجم نمونه و اهمیت آن

همان طور که بیان شد، عمل تعیین حجم نمونه را باید در هر مسئله با توجه به شرایط و خصوصیات آن مسئله انجام داد. بر این اساس، مبحث تعیین حجم نمونه در طیف گسترده‌ای از مسائل آماری مطرح می‌شود. مسائلی از قبیل مطالعات مربوط به میانگین، مطالعات همبستگی، مطالعات تحلیل بقا، مطالعات مورد شاهدی و غیره از جمله مسائل پرکاربرد در انواع پژوهش‌ها هستند که هر کدام روش‌ها و نکات خاص خود در تعیین حجم نمونه را دارند.

 در مطلب حاضر، فقط مقدمه‌ای کوتاه بر لزوم تعیین حجم نمونه و اهمیت دقت در انجام آن بیان شد. امروزه برای انتشار نتایج تحقیقات در منابع معتبر، در هر شاخه از علوم انسانی یا علوم تجربی، علاوه بر نیاز به کیفیت مطالب در حوزه مورد نظر، نیازمند به معتبر بودن روش‌های آماری به‌کارگرفته شده در آن مطالعات هستیم.

به عنوان مثال، داوران ژورنال‌های علمی معتبر، بخش‌های مربوط به روش‌های آماری مقاله را به دقت و با دید نقادانه مطالعه می‌کنند و در مورد آن به ارائه‌ی نظر می‌پردازند. در این میان، حجم نمونه و چگونگی انتخاب آن نیز یکی از مواردی است که نویسندگان مقاله باید دلایل و توضیحات معتبری برای آن داشته باشند.

 لذا آگاهی و تسلط پژوهش‌گران حوزه‌های مختلف به بحث تعیین حجم نمونه، امری مهم و اجتناب‌ناپذیر است. شما می توانید برای دستیابی به حجم نمونه از خدمات شرکت های آماری استفاده کنید. در مطالب آینده، بحث تعیین حجم نمونه در هر کدام از مسائل آماری مختلف برای پژوهش‌گران فعال در زمینه‌های مختلف، به تفصیل بیان خواهد شد.در ادامه، به معرفی و بررسی یکی از روش‌های معروف در تعیین حجم نمونه پرداخته می‌شود.

فرمول کوکران

در مسیر انجام پژوهش، قسمتی از فصل سوم پایان نامه یا رساله به توضیح جامعه آماری، نمونه آماری، روش نمونه‌گیری و حجم نمونه مناسب اختصاص دارد. حال آن‌که این موضوع باید در اولین قدم و در زمان تهیه پروپوزال پژوهشی مورد توجه قرار گیرد. پژوهشگر بایستی جامعه هدف مورد نظر خود را به صورت شفاف تعریف نماید، تعداد کل افراد که در جامعه قرار دارند را مشخص کند و با توجه به روش انجام پژوهش نسبت به محاسبه حجم نمونه مناسب و اختصاص روش نمونه‌گیری بهینه اقدام کند.

یکی از روش‌های پرکاربرد در تعیین حجم نمونه، استفاده از فرمول کوکران است. این فرمول در دو حالت مورد استفاده قرار می‌گیرد و در اکثر پایان‌نامه‌ها و رساله‌ها می‌تواند مورد استفاده قرار بگیرد اما استفاده نابجا از این فرمول پیامدهایی در پی دارد که پیش‌تر از آن یاد کردیم. قبل از این که وارد بحث محاسبه حجم نمونه با استفاده از فرمول کوکران شویم در ابتدا تعریف جامعه آماری و فرآیند نمونه‌گیری را یادآوری می‌کنیم.

جامعه آماری مجموعه‌ای از افراد و یا اشیا هستند که حداقل در یک صفت اشتراک دارند. نمونه‌گیری در واقع انتخاب نمونه‌ای از جامعه آماری است که نمونه انتخابی باید ویژگی‌های خاصی داشته باشد تا بتوان نتایج حاصل از نمونه را برای جامعه آماری تعمیم داد.

تعیین حجم نمونه با فرمول کوکران

تعیین اندازه نمونه اهمیت فراوانی در قابلیت تعمیم نتایج آزمون به جامعه دارد. روش‌های مختلفی جهت تعیین اندازه نمونه وجود دارد که دقیق‌ترین روش‌ها، روش‌های ریاضی جهت محاسبه اندازه نمونه است. یکی از این روش‌ها استفاده از فرمول کوکران است. همانطور که می‌دانیم جامعه آماری می‌تواند مقداری معلوم باشد مانند دانش‌آموزان مقطع دبستان شهرستان مشهد و یا مدیران ارشد بانک صادرات شهرستان بیرجند و همچنین می‌تواند مقداری نامعلوم باشد مانند افراد مراجعه‌کننده به بیمارستان‌ها و درمانگاه‌ها. با استفاده از فرمول کوکران می‌توانیم برای هر دو جامعه آماری معلوم و نامعلوم، حجم نمونه را تعیین کنیم.

1. حجم نمونه وقتی حجم جامعه آماری معلوم است.
2. حجم نمونه وقتی حجم جامعه آماری نامعلوم است.

 فرمول کوکران امکان محاسبه‌ی حجم مناسب نمونه بر اساس سطح مشخصی از دقت، سطح مشخصی از اطمینان و نسبت اعضایی که دارای صفت خاصی هستند می‌دهد. فرمول کوکران عبارت است از:

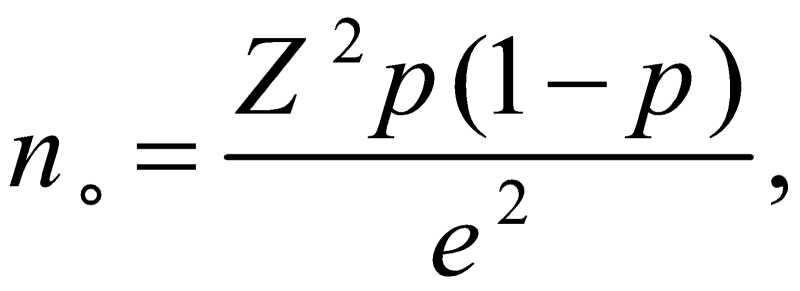
که در آن 

p نسبت (براوردشده) از افرادی از جامعه است که دارای صفت مورد نظر هستند؛

e سطح دلخواه دقت (حاشیه خطا) است. این مقدار تعیین می‌کند که مقدار نسبت براوردشده حداکثر چقدر با مقدار واقعی آن تفاوت داشته باشد؛

Z صدک مرتبه است که از جدول توزیع نرمال پیدا می‌شود ونیز همان احتمال خطای نوع یک است. مقداررا همان سطح اطمینان می‌نامند.

فرمول کوکران برای جامعه نامحدود

در این قسمت می بینید که فرمول کوکران برای جامعه نامحدود چگونه برقرار است.

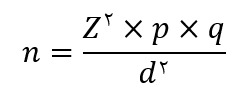
مثال کاربردی برای محاسبه فرمول کوکران برای جامعه نامحدود

فرض کنید در حال انجام مطالعه بر روی افراد مقیم در یک شهر بزرگ هستیم، و می‌خواهیم تعداد افرادی را که صبح‌ها در خانه به صرف صبحانه می‌پردازند بدانیم. اطلاعات چندانی در مورد این که از کجا شروع کنیم نداریم و لذا فرض می‌کنیم نیمی از خانواده‌ها در خانه صبحانه را صرف می‌کنند. در این صورت p=0.5 و واریانس حداکثر را خواهیم داشت. حال فرض کنید می‌خواهیم سطح اطمینان 95 درصد داشته باشیم، و دقت هم 5 درصد باشد. در سطح اطمینان 95 درصد مقدار Z برابر با 1.96 است، لذا داریم:

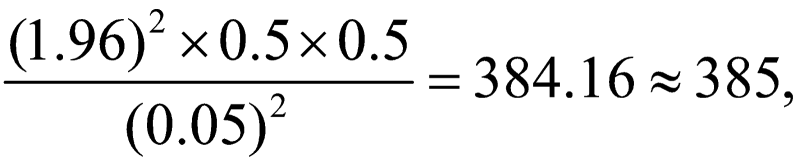
فرمول کوکران برای جامعه محدود (تصحیح فرمول کوکران برای محاسبات حجم نمونه در جوامع کوچک)

فرمول کوکران برای مواقعی که با جوامع بزرگ (جامعه نامحدود) سر و کار داریم به کار می‌آید. اگر حجم نمونه ثابت باشد، اطلاعاتی که از یک جامعه‌ی کوچک به دست می‌آید بیشتر از جامعه‌ی بزرگ است. لذا در فرمول کوکران، تصحیحی در نظر گرفته شده که در صورت کوچک بودن حجم جامعه، عدد به دست آمده از این فرمول را کاهش می‌دهد.

دقت کنید که جوامع با حجم بزرگ به عنوان جوامع نامحدود و جوامع با حجم کوچک به عنوان جوامع محدود در نظر گرفته می‌شوند. در این حالت، حجم نمونه عبارت است از:

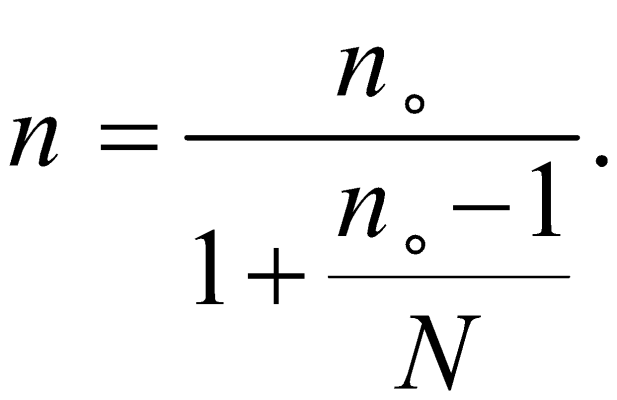
در فرمول بالا، N حجم جامعه،

حجم نمونه‌ در فرمول اصلی کوکران و n حجم نمونه‌ی تصحیح‌شده و جدید است.

در مثال قبل، اگر تعداد کل خانواده‌ها در جامعه‌ی مورد نظر 1000 باشد، آن گاه

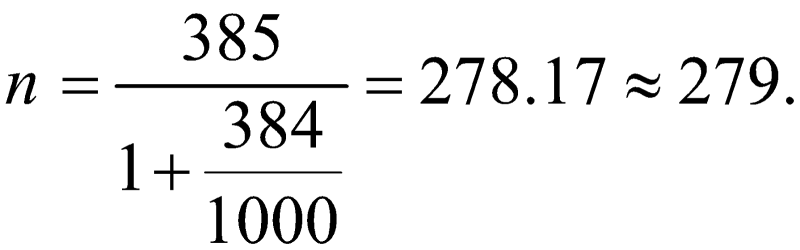
نکات مهم در استفاده از فرمول کوکران برای تعیین حجم نمونه

1- در صورت معلوم نبودن p می‌توان مقدار آن را از طریق یک نمونه اولیه (پایلوت) براورد کرد. بدین صورت که ابتدا نمونه‌ای کوچک (مثلاً با حجم 20 تا 30) از جامعه فراهم و مقدار p را به ازای آن براورد می‌کنیم. سپس از مقدار براوردشده در فرمول کوکران استفاده می‌کنیم.

2- استفاده از فرمول مورگان برای تعیین حجم نمونه تنها زمانی مجاز است که به دنبال براورد نسبت یک صفت در جامعه هستیم. استفاده از این فرمول برای اهدافی غیر از این مورد، اشتباه و غیرمنطقی است.

محاسبه تعیین حجم نمونه با فرمول کوکران در اکسل

فایلی که برای دانلود در اختیار شما قرار داده شده به شما کمک می کند تا با وارد کردن اطلاعات پایان نامه خود بتوانید، حجم نمونه خود را دریافت کنید. برای دانلود این فایل بر روی عبارت تعیین حجم نمونه با فرمول کوکران در اکسل کلیک کنید.

در چه صورت نمی‌توان از فرمول کوکران استفاده کرد؟

از آنجایی که شیوه درست تعیین حجم نمونه برای هر مطالعه تحقیقاتی حائز اهمیت است، بنابراین نمی‌شود در تمام موارد از فرمول کوکران برای انتخاب حجم نمونه استفاده کرد. به‌عنوان مثال در بعضی تحقیقات کیفی تعداد 15 تا 30 نفر برای حجم نمونه کفایت می‌کند و یا در بعضی تحقیقات تعداد حجم نمونه نامشخص است و تا رسیدن به اجماع نظر باید ادامه پیدا کند. همچنین در مواردی مانند طرح‌های آزمایش پیش‌آزمون و پس‌آزمون، تحلیل سلسله مراتبی، در بعضی موارد مدلسازی معادلات ساختاری و … نمی‌توان از فرمول کوکران استفاده کرد. معمولا در نظرسنجی‌ها و افکارسنجی‌ها به شرط برقراری سایر شرایط استفاده از فرمول کوکران مجاز است.

جدول مورگان

جدول مورگان از محاسبه‌ی حجم نمونه به ازای مقادیر مشخص پارامترها در فرمول کوکران به دست آمده است. در این جدول، مقدار p برابر با 0.5، مقدار برابر با 0.05 و مقدار e نیز برابر با 0.05 قرار داده شده و سپس به ازای مقادیر مختلف N مقادیر حجم نمونه محاسبه و در جدولی ارائه شده است. این مقادیر برای پارامترها، منجر به بیشترین حجم نمونه ممکن می‌شود و لذا استفاده از این جدول که متأسفانه تعداد زیادی از کارهای پژوهشی نیز از آن بهره می‌گیرند، درست نیست.

دلایل این امر نیز پیشتر مطرح شد. اول آن که جدول مورگان (که برگرفته از فرمول کوکران است) فقط برای مواردی که براورد نسبتی از یک صفت در جامعه مورد نظر باشد مجاز است. دوم آن که هر مسئله شرایط خاص خود را دارد و بر اساس آن شرایط باید مقادیر پارامترها تعیین گردد، نه آن که مقادیر یکسانی از پارامترها برای همه‌ی مسائل مورد استفاده قرار گیرد.

موضوع تعیین حجم نمونه و انتخاب یک نمونه مناسب، یکی از مسائلی است که اکثر پژوهشگران در شروع مطالعه خود با آن سر و کار دارند. همانطور که می‌دانید تعداد حجم نمونه باید طوری انتخاب شود که قابل تعمیم به کل جامعه آماری باشد. بر هیچ‌کس پوشیده نیست که چنانچه حجم نمونه کمتر از میزان لازم در نظر گرفته شود، ممکن است نتایج استنباط شده از آن در مورد جامعه از دقت کافی برخوردار نباشد.

اما این برداشت نادرست نیز وجود دارد که حجم نمونه هر چه بزرگ‌تر باشد (یعنی هر چه حجم نمونه به حجم جامعه نزدیک‌تر باشد)، وضعیت بهتری برای مطالعه انتظار می‌رود. باید توجه داشت که همواره در نمونه‌های با حجم بزرگ، تضمینی برای اتخاذ تصمیم منطبق بر واقعیت وجود ندارد. بنابراین مشکلات استفاده از حجم نمونه بزرگ در مطالعات بر همگان آشکار نیست.

روش تعیین حجم نمونه یکی از مهم ترین مباحث در پرپوزال است.بسیاری از افراد به دلیل نداشتن تخصص لازم در رشته های مختلف نمی توانند روش مناسب را انتخاب کنند. به منظور مشورت با افراد متخصص در تحلیل آماری پایان نامه پل ارتباطی را در سایت آمار پیشرو ایجاد کردیم که شما می توانید از نظر خبرگان استفاده کنید. برای بهره مندی از افراد متخصص به صورت رایگان به بخش مشاوره آماری رایگان مراجعه کنید.

چنانچه به دنبال آموزش های بیشتر در مسیر تحلیل آماری پایان نامه هستید، میتوانید مباحث معادلات ساختاری، آنالیز واریانس ، آزمون t  را در بلاگ سایت آمار پیشرو ببینید. برای با خبر شدن از مطالب جدید آماری و بروز نگه داشتن علم آماری خود می توانید صفحه اینستاگرام آمار پیشرو را دنبال کنید.

در این مقاله سعی کردیم نکات مهم تعیین حجم نمونه را برای شما شرح دهیم. اما چنانچه در مسیر تحلیل آماری پایان نامه نیاز به خدمات آماری مختلف در حوزه پایان نامه هستید می توانید شرح خدمات این حوزه را در بخش تحلیل آماری پایان نامه مشاهده کنید. با تکمیل فرم در بخش ثبت سفارش می توانید بخش آماری پایان نامه خود را به افراد خبره در گروه آمار پیشرو بسپارید.