تحلیل مسیر Path Analysis چیست؟-با مثال هایی ملموس

[block id=”breadcrumb”]

تحلیل مسیر Path Analysis چیست؟

تحلیل مسیر تکنیکی آماری است که با استفاده از معادلات رگرسیون خطی استاندارد (معادلات رگرسیون خطی بر حسب ضرایب رگرسیون استاندارد) به میزان انطباق یک مدل علی نظری با واقعیت (داده‌ها) می‌پردازد. به عبارت دیگر تحلیل مسیر تکنیکی برای آزمون تجربی مدل علی نظری است. علاوه بر این اگر مدل علی نظری با داده‌های جمعیتی معین انطباق داشته باشد می‌توان انواع اثرات (اثر مستقیم و غیرمستقیم و کاذب و خالص) تک تک متغیرهای مستقل بر متغیر وابسته مدل علی نظری را نیز حساب کرد.

 بهتر است قبل از هز چیزی بهتر است که به مطلب رگرسیون سری بزنید و مفهوم آن را دریافت کنید.

تحلیل مسیر یکی از خدمات تحلیل آماری است که شما می توانید آن را خود انجام دهید یا به یک شرکت آماری بسپارید، اگر وقت لازم را دارید می توانید در این مطلب کامل یک مثال ملمویس را حل کردیم که کامل آموزش ببینید، اما چنانچه وقت کافی ندارید می توانید این خدمت را به عنوان یکی از خدمات تحلیل آماری با تعریف پروژه آماری از بخش خدمات سفارش دهید.

مدل علی نظری Theoretical Causal Model چیست؟

مدل علی نظری مجموعه‌ای از متغیرهای مستقل (علت) و متغیر وابسته (معلول) و روابط بین آنهاست که بر اساس چارچوب نظری و استدلال نظری ساخته می‌شود. تحلیل مسیر مختص آزمون مدل علی نظری است که روابط متغیرها در آن مدل یک‌سویه است. به عبارت دیگر تحلیل مسیر برای آزمون مدلی که متضمن روابط متقابل بین متغیرهاست به کار نمی‌رود.

آزمون مدل علی در تحلیل مسیر مستلزم ترسیم مدل علی به صورت نموداری است به نام نمودار مسیر که متغیرها را بر حسب نظم و ترتیب و توالی علی نظری نشان می‌دهد (مانند شکل1). عنوان نمودار در نمودار مسیر تأکیدی است بر یک‌سویه بودن رابطه متغیرها و از همین روست که تکنیک آماری آزمون مدل علی نظری را تحلیل مسیر می‌خوانند.

تعریف 1: تحلیل مسیر تکنیکی است آماری برای آزمون تجربی مدل علی نظری.

نمودار مسیر Path Diagram چیست؟

در نمودار مسیرمتغیرها بر حسب نظم و ترتیب و توالی علی نظری از چپ به راست قرار می‌گیرند. روابط بین متغیرها و نظم و ترتیب و تقدم و تأخر آنها هم به استدلال نظری متکی است. رابطه علی هر متغیری با متغیر دیگر را یک پیکان نشان می‌دهد که آن دو را به هم وصل می‌کند. پیکان مبین مسیر علی متغیر علت بر متغیر معلول است. متغیر علت در انتهای پیکان قرار می‌گیرد و متغیر معلول در نوک پیکان.

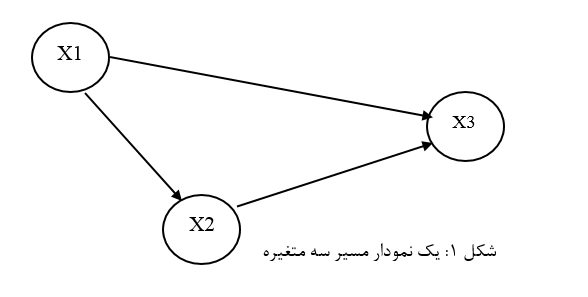
به عنوان مثال نمودار مسیر شکل 1 نشان می‌دهد که دو متغیر مستقل X1 و X2 بر متغیر وابسته X3 اثر علی دارند. علاوه بر آن متغیر مستقل X1 بر متغیر X2 نیز اثر علی دارد.

متغیرهای درونزاد Endogenius و برونزاد Exogenous به چه معناست ؟

در نمودار مسیر به متغیر مستقلی که خود متأثر از متغیر یا متغیرهای مستقل دیگر در نمودار مسیر است و در واقع وابسته متغیرهای مستقل دیگر است متغیر درونزاد اطلاق می‌شود. به متغیر مستقلی هم که متأثر از هیچ متغیر مستقلی در نمودار مسیر نیست متغیر برونزاد گفته می‌شود.

متغیر وابسته نمودار مسیر هم‌متغیری است که متأثر از همه متغیرهای مستقل‌هاست اما بر هیچ متغیری اثر ندارد.

تعریف 2: مدل علی نظری عبارت است از یک دسته متغیر مستقل (علت) و یک متغیر وابسته (معلول) و روابط نظری بین آنها.

در نمودار مسیر شکل 1 متغیر مستقل X1 که معلول هیچ متغیر مستقلی در نمودار مسیر نیست متغیر برونزاد است و متغیر مستقل X2 که متأثر از متغیر X1 است متغیر درونزاد به شمار می‌آید و متغیر X3 هم که بر هیچ متغیری اثر ندارد متغیر وابسته است.

تعریف 3: متغیر برونزاد متغیر مستقلی است که متأثر از هیچ متغیر مستقل نمودار مسیر نیست و متغیر درونزاد متغیر مستقلی است که حداقل متأثر از یکی از متغیرهای مستقل نمودار مسیر است.

مفروضات تحلیل مسیر

تحلیل مسیر مبتنی بر مفروضاتی به این شرح است:

• متغیرها کمی و یا دو وجهی‌اند.
• روابط متغیرها خطی و جمع پذیر است و شامل روابط منحنی و تعاملی نمی‌شود.
• جریان علیت در متغیرها یکطرفه است.
• باقیمانده یک متغیر با باقیمانده‌های سایر متغیرها همبسته نیست.

انجام تحلیل مسیر منوط به تحقق این مفروضات و شرایط است. متغیرهای مستقل باید کمی و یا دووجهی باشند و رابطه متغیرهای کمی با متغیر وابسته نیز خطی باشد. از این متغیرهای مستقل نباید به صورت تعاملی اثر مضاعفی بر متغیر وابسته داشته باشند.

فرض یکطرفه‌بودن جریان علیت در متغیرها نیز بدان معناست که بر اساس استدلال نظری روابط علی بین متغیرها باید یکطرفه باشد و متغیرهایی را که با هم رابطه متقابل دارند نمی‌توان وارد نمودار مسیر کرد و مورد تحلیل قرار داد. فرض آخر نیز بدان معناست که همبستگی باقیمانده هر متغیر با باقیمانده‌های سایر متغیرها باید صفر باشد.

متغیرهای ظاهری را هم نمی‌توان در تحلیل مسیر به کار برد چه آنها طبقات یک متغیرند و از این رو همبستگی بالایی با هم دارند اما این همبستگی‌ها رابطه علی نیست که بتوان وارد تحلیل مسیر کرد.

اجرای آزمون نمودار مسیر به صورت مرحله به مرحله

برای آزمون تجربی یک نمودار مسیر (مدل علی نظری) بعد از گردآوری داده‌ها از جمعیتی معین (یا نمونه‌ای احتمالی از آن) و اطمینان از تحقق مفروضات تحلیل مسیر برای متغیر وابسته و هر یک از متغیرهای درونزاد یک تحلیل رگرسیون خطی انجام می‌دهیم.

چنانچه ضرایب رگرسیون تمام رگرسیون‌های خطی معنادار بود (سطح معناداری آنها مساوی 05/0 یا کمتر بود) و از طرف دیگر همبستگی متغیرهایی که در نمودار مسیر رابطه‌ای با هم ندارند صفر شد نمودار مسیر با واقعیت (داده‌های جمعیتی معین) انطباق دارد. در این صورت مدل علی مورد تحلیل برازنده آن جمعیت معین است. به عبارت دیگر مدل علی برازندگی دارد.

نکته 1: آزمون تجربی نمودار مسیر مستلزم تشکیل یک معادله رگرسیون خطی برای متغیر وابسته و یک معادله رگرسیون خطی برای هر یک از متغیرهای مستقل درونزاد است.

به طور خلاصه آزمون تجربی یک نمودار مسیر مستلزم سه مرحله است:

مرحله 1 وارسی مفروضات

مرحله 2 تحلیل رگرسیون خطی

مرحله 3 نتیجه‌گیری درباره برازندگی مدل

در اینجا برای نشان‌دادن مراحل عملی آزمون یک نمودار مسیر از چند مثال ساده استفاده می‌کنیم.

مثال 1: فرض کنیم محققی بر اساس چارچوب نظری و استدلال نظری مدلی علی به صورت نمودار مسیر شکل 1 ارائه کرده است که نشان می‌دهد دو متغیر مستقل X1 و X2 بر متغیر وابسته X3 اثر علی دارند. همچنین متغیر X1 بر متغیر X2 نیز اثر علی دارد. وی داده‌های مقتضی برای سنجش متغیرهای نمودار مسیر را نیز از نمونه‌ای احتمالی از جمعیتی معین (گیریم ساکنان شهر خوشاب) گردآوری کرده است (جدول1).

برای انجام تحلیل مسیر در گام اول مفروضات آن را وارسی می‌کنیم.

مرحله 1 وارسی مفروضات

همانطور که در جدول 1 می‌بینیم هر سه متغیر مستقل X1 و X2 وX3 کمی‌اند (فرض اول).

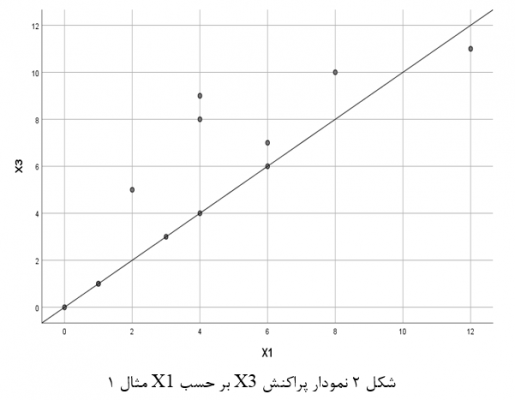
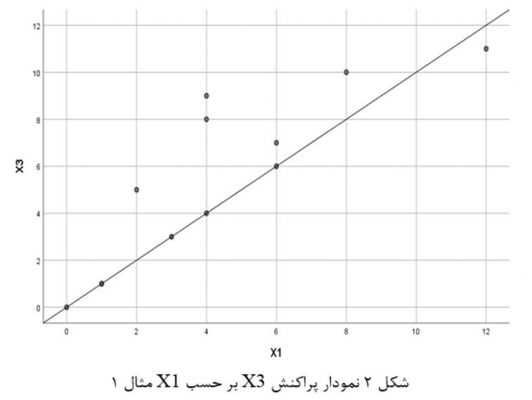
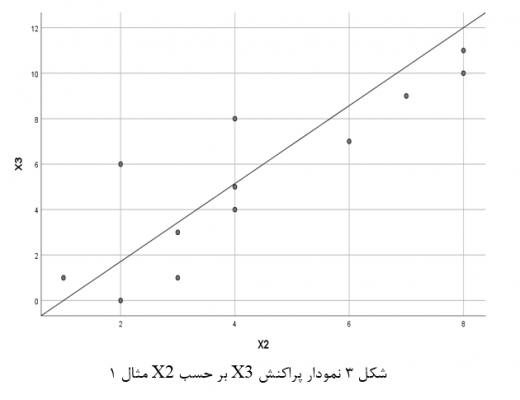
در شکل 2 نیز می‌بینیم در نمودار پراکنش متغیر وابسته X3 بر حسب متغیر X1 رابطه آنها خطی است. در شکل 3 هم می‌بینیم در نمودار پراکنش متغیر X3 بر حسب متغیر X2 رابطه آنها خطی است. در شکل 4 هم می‌بینیم در نمودار پراکنش متغیر درونزاد X2 با متغیر برونزاد X1 رابطه آنها خطی است (فرض دوم).

جمع‌پذیری روابط را نیز مفروض می‌گیریم. فرض یکطرفه‌بودن جریان علیت در متغیرها نیز مبتنی بر استدلال نظری محقق است (فرض سوم).

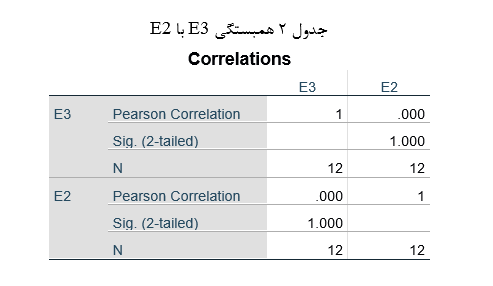
در جدول 2 هم می‌بینیم همبستگی E3 که باقیمانده رگرسیون خطی X1 با X2 و X3 است با E2 که باقیمانده رگرسیون خطی X2 با X1 است صفر است (فرض چهارم).

حال با حصول اطمینان از مفروضات تحلیل مسیر در گام دوم به تحلیل‌های رگرسیون خطی مقتضی می‌پردازیم.

مرحله 2 تحلیل‌های رگرسیون خطی

بیشتر بخوانید: رگرسیون خطی ساده چیست؟

تحلیل مسیر مثال 1 مستلزم دو تحلیل (معادله) رگرسیون خطی است: یکی رگرسیون خطی متغیر وابسته X3 با دو متغیر مستقل X1 وX2:

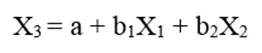
و دیگری رگرسیون خطی متغیر مستقل درونزاد X2 با متغیر مستقل X2 :

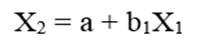
تحلیل رگرسیون خطی متغیر وابسته X3 با دو متغیر مستقل X1 وX2 (جدول 3) نشان می‌دهد هر دو متغیر مستقل با متغیر وابسته دارای رابطه معنادار هستند:

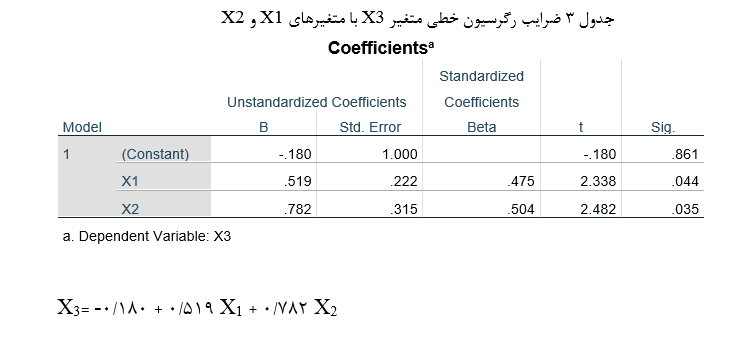
تحلیل رگرسیون خطی متغیر مستقل درونزاد X2 با متغیر مستقل X1 هم نشان می‌دهد آن دو با هم رابطه معنادار دارند (جدول 4):

بعد از تحلیل‌های رگرسیون خطی مقتضی نمودار مسیر در گام سوم درباره برازندگی نمودار مسیر (مدل علی) نتیجه‌گیری می‌کنیم.

مرحله 3 نتیجه‌گیری درباره  برازندگی مدل

همان‌طور که پیشتر به میان آمد هرگاه ضرایب رگرسیون تمام رگرسیون‌های خطی مقتضی معنادار بود (سطح معناداری آنها مساوی 05/0 یا کمتر بود) و همبستگی متغیرهایی که در نمودار مسیر رابطه‌ای با هم ندارند صفر شد نمودار مسیر با واقعیت (داده‌های جمعیتی معین) انطباق دارد.

درباره نمودار مسیر مثال 1 که ضرایب رگرسیون هر دو رگرسیون‌های خطی مقتضی معنادار بود نتیجه می‌گیریم نمودار مسیر مثال 1 با واقعیت (داده‌های جمعیتی معین) انطباق دارد. این بدان معناست که مدل علی محقق (شکل 1) برازنده آن جمعیت است. به عبارت دیگر نمودار مسیر مثال 1 دارای برازندگی است.

هرگاه نمودار مسیر دارای برازندگی در جمعیت مورد آزمون بود (مانند نمودار مسیر شکل 1) میزان برازندگی آن را مشخص کرده و ضرایب مسیر مدل را وارد نمودار مسیر می‌کنیم.

اما چنانچه ضریب رگرسیون یکی از متغیرهای مستقل در یکی از تحلیل‌های رگرسیون‌های خطی معنادار نبود یا بین متغیرهایی که در نمودار مسیر رابطه‌ای با هم ندارند همبستگی وجود داشت نمودار مسیر با واقعیت انطباق ندارد و فاقد برازندگی در جمعیت مورد آزمون تأیید نمی‌شود.

مثال 2: فرض کنیم محققی بر اساس چارچوب نظری و استدلال نظری یک مدل علی به صورت نمودار مسیر شکل 5 ارائه کرده است که نشان می‌دهد دو متغیر مستقل X1 وX2 بر متغیر وابسته X3 اثر علی دارند و بین متغیر X1 و X2 نیز رابطه‌ای وجود ندارد.

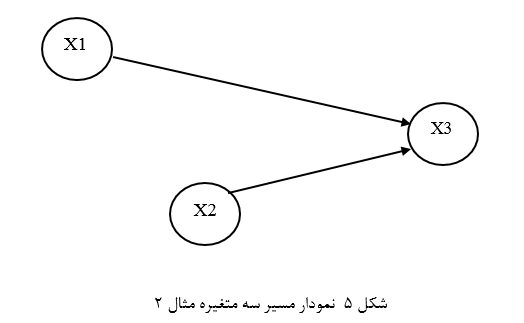
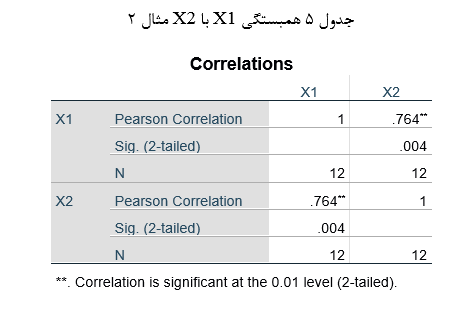
حال اگر همان داده‌های مثال 1 را برای آزمون نمودار مسیر وی به کار ببریم چون بین دو متغیر مستقل X1 وX2 همبستگی وجود دارد (جدول 5) نمودار مسیر مذکور با واقعیت انطباق ندارد و فاقد برازندگی در جمعیت مورد آزمون است. به عبارت دیگر این نمودار مسیر در این آزمون تأیید نمی‌شود.

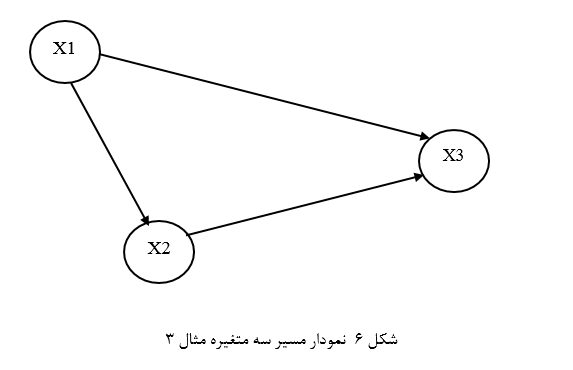
مثال 3: فرض کنیم محققی بر اساس چارچوب نظری و استدلال نظری یک مدل علی به صورت نمودار مسیر شکل 6 ارائه کرده است که نشان می‌دهد دو متغیر مستقل X1 وX2 بر متغیر وابسته X3 اثر علی دارند. همچنین متغیر X1 هم بر متغیر X2 اثر علی دارد. وی داده‌های مقتضی برای سنجش متغیرهای نمودار مسیر را نیز از نمونه‌ای احتمالی از جمعیتی معین (گیریم ساکنان شهر قشلاق) گردآوری کرده است (جدول 6).

تحلیل رگرسیون خطی متغیر وابسته X3 با دو متغیر مستقل X1 وX2 (جدول 7) نشان می‌دهد هر دو متغیر مستقل رابطه معناداری با متغیر وابسته دارند. اما تحلیل رگرسیون خطی متغیر مستقل درونزاد X2 با متغیر مستقل X1 نشان می‌دهد بین آن دو رابطه‌ای وجود ندارد (جدول 8).

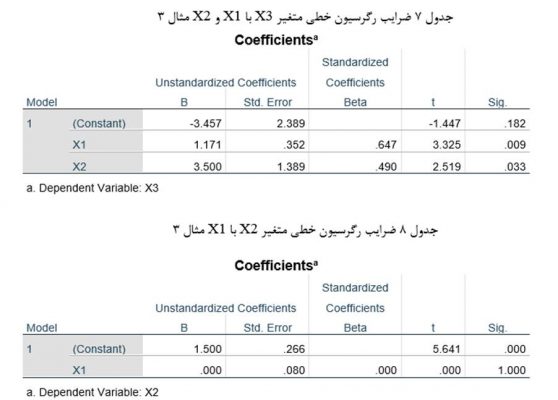
در اینجا نمودار مسیر مذکور با واقعیت انطباق ندارد چون فرض شده بود متغیر X1 بر متغیر X2 اثر علی دارد. بنابراین مدل مذکور فاقد برازندگی در جمعیت مورد آزمون است. به عبارت دیگر نمودار مسیر مثال 3 در این آزمون تأیید نمی‌شود.

شاخص برازندگی مدل علی

در تحلیل مسیر ضریب تعیین (R²)  متغیر وابسته مشخص می‌کند که یک مدل علی نظری دارای برازندگی چقدر با واقعیت (داده‌ها) انطباق دارد. از این رو ضریب تعیین رگرسیون خطی متغیر وابسته با متغیرهای مستقل شاخص برازندگی مدل علی نظری به شمار می‌آید.

ضریب تعیین هم مبین آن است که چه نسبتی از تغییر کل متغیر وابسته ناشی از مجموعه متغیرهای مستقل است. حداکثر مقدار ضریب تعیین یک و حداقل آن صفر است. هر چه مقدار ضریب تعیین به یک نزدیک‌تر باشد برازندگی مدل علی نظری بیشتر است.

در جایی که نمودار مسیر همه متغیرهای مستقل مؤثر در متغیر وابسته را در برگیرد ضریب تعیین به حداکثر مقدار خود (یک) می‌رسد و بدان معناست که همه تغییر متغیر وابسته ناشی از متغیرهای مستقل است و برازندگی مدل علی نظری کامل است. در جایی هم که معادله رگرسیون خطی هیچ یک از متغیرهای مستقل مؤثر بر متغیر وابسته در برنگیرد ضریب تعیین صفر می‌شود که بدان معناست هیچ نسبتی از تغییر متغیر وابسته ناشی از متغیرهای مستقل نیست و مدل علی فاقد برازندگی است.

نمودار مسیر مثال 1 دارای برازندگی بود. بنابراین ضریب تعیین رگرسیون خطی متغیر وابسته آن با متغیرهای مستقل بیانگر میزان برازندگی آن نمودار مسیر است. در این مدل ضریب تعیین رگرسیون خطی متغیر وابسته X1 وX2 حدود 85/0 است (جدول 9) که نشان می‌دهد اگر روابط علی بین متغیرها وجود داشته باشد 85/0 از تغییر متغیر وابسته X3 ناشی از متغیرهای مستقل X1 وX2 است.

ضریب مسیر Path Coefficient چه مفهوم و کاربردی دارد؟

ضریب مسیرضریب رگرسیون استاندارد متغیر علت با متغیر معلول در معادله رگرسیون خطی است که نمودار مسیر اقتضا می‌کند و مبین اثر مستقیم متغیر علت بر متغیر معلول است. در جایی که نمودار مسیر دارای برازندگی در جمعیت مورد آزمون بود ضرایب مسیر را وارد نمودار مسیر می‌کنیم (مانند شکل 7).

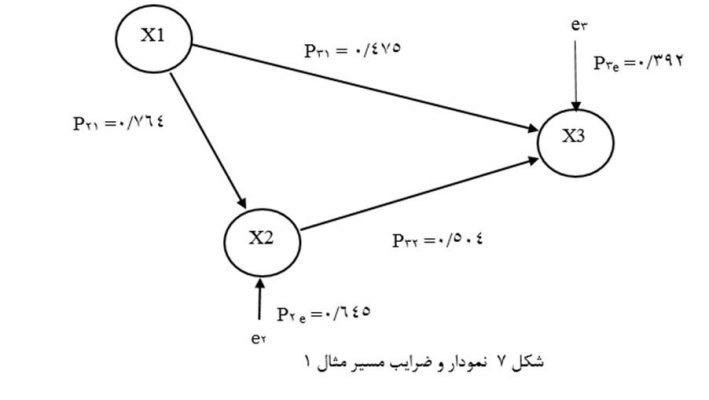
هر ضریب مسیر را با نماد P_ij نشان می‌دهیم. در نماد P_ij اندیس i ام مبین متغیر معلول و اندیس j ام مبین متغیر علت است. برای اجتناب از شلوغی نمودار مسیر متغیرها را به ترتیب رابطه علت و معلولی شماره‌گذاری کرده و در اندیس نماد ضریب مسیر نیز فقط شماره متغیرها را به کار می‌بریم.

به عنوان مثال در شکل 7 ضریب مسیر P₃₁ مبین ضریب رگرسیون استاندارد متغیر مستقل X1 با متغیر وابسته X3 است و ضریب مسیر P₃₂ مبین ضریب رگرسیون استاندارد متغیر مستقل X2 با متغیر وابسته X3 .

مقادیر ضرایب مسیر هم از رگرسیون خطی که مدل علی اقتضا می‌کند به دست می‌آید. به عنوان مثال در نمودار مسیر شکل 7 ضرایب مسیر از رگرسیون خطی متغیر X3 با متغیرهای X1 و X2 که نتایج آن در جدول 3 آمده است و رگرسیون خطی متغیر X2 با متغیر X1 که نتایج آن در جدول 4 ارائه شده است به دست می‌آید.

طبق جدول 3 ضریب رگرسیون استاندارد X1 با X3 معادل 475/0 است. پس در نمودار مسیر شکل 4 مقدار ضریب مسیر P₃₁ را 475/0 درج می‌کنیم. همینطور مقدار ضریب رگرسیون استاندارد X2 با X3 را که 504/0 است برای ضریب مسیر P₃₂ می‌نویسیم. مقدار ضریب مسیر P₂₁ هم مقدار ضریب رگرسیون استاندارد متغیر مستقل X1 با متغیر مستقل درونزاد X2 است که مطابق جدول 4 معادل 764/0 است.

تعریف 4: ضریب مسیر ضریب رگرسیون استاندارد متغیر علت با متغیر معلول در معادله رگرسیون خطی نمودار مسیر است.

ضریب مسیر باقیماندهResidual Path Coefficient چیست؟

ضریب مسیر باقیمانده  ضریب مسیر عوامل ناشناخته است. عوامل ناشناخته هم متغیرهایی هستند که مدل علی آنها را در بر نگرفته است. ترسیم آنها در نمودار برای نشان‌ دادن سهم عوامل ناشناخته در متغیر معلول یا نسبتی از تغییر متغیر معلول است که در مدل علی تبیین نشده باقی مانده است. عوامل ناشناخته متغیر معلول X_j را با نماد e_j و ضریب مسیر آن را با نماد P_je نشان می‌دهیم. به عنوان مثال در شکل 7 باقیمانده متغیر X3 با نماد ₃e نشان داده شده است و ضریب مسیر آن با نمادP_e3.

ضریب مسیر باقیمانده متغیر معلول X_j با نماد P_je عبارت است از جذر نسبت تغییر متغیر معلول که در نمودار مسیر تبیین نشده باقیمانده است:

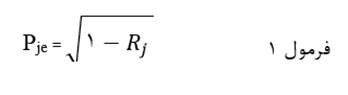
که در آن R_j ضریب تعیین مقدار معلول X_j است.

به عنوان مثال ضریب مسیر باقیمانده متغیر X3 در نمودار مسیر شکل 7 با توجه به این که مقدار ضریب تعیین رگرسیون X3 با دو متغیر مستقل X1 و X2 معادل 846/0 است (جدول 9) عبارت است از:

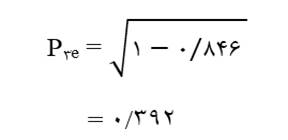
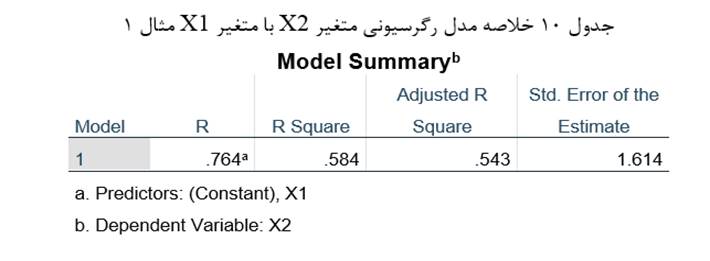
و ضریب مسیر باقیمانده متغیر X2 با توجه به این که مقدار ضریب تعیین رگرسیون آن متغیر با متغیر X1 معادل 584/0 است (جدول 10) عبارت است از:

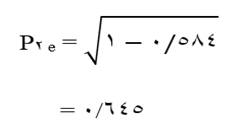
اثرات متغیرهای مستقل کدامند؟

در مدل علی نظری دارای برازندگی که مدلی است که با داده‌های جمعیتی معین انطباق دارد می‌توان اثرات مختلف تک تک متغیرهای مستقل بر متغیر وابسته را نیز مشخص کرد: اثر مرتبه صفر و اثر مستقیم و اثر غیرمستقیم و اثر کاذب و اثر خالص.

اثر مرتبه صفر Zero-Order Effect

اثر مرتبه صفریک متغیر مستقل بر متغیر وابسته همبستگی آن دو متغیر بدون به حساب آوردن سایر متغیرهای نمودار مسیر است. به عبارت دیگر اثر مرتبه صفر متغیر مستقل بر متغیر وابسته همان همبستگی آن دو متغیر است.

تعریف 5: ضریب مسیر باقیمانده ضریب مسیر متغیرهای ناشناخته است که در مدل علی قرار ندارند.

در تحلیل مسیر اثر مرتبه صفر یک متغیر مستقل بر متغیر وابسته به سه اثر جداگانه تقسیم می‌شود: اثر مستقیم و اثر غیرمستقیم و اثر کاذب. به عبارت دیگر اثر مرتبه صفر یک متغیر مستقل بر متغیر وابسته با نماد r_ij عبارت است از مجموع سه اثر مذکور:

که درآن p_ij اثر مستقیم متغیر مستقل X_j بر متغیر وابسته X_i و ir_ij اثرغیرمستقیم و sr_ij اثر کاذب آن.

نکته 2: اثر مرتبه صفر یک متغیر مستقل بر متغیر وابسته همبستگی آن دو متغیر است که در نمودار مسیر به سه اثر مستقیم و غیرمستقیم و کاذب تجزیه می‌شود.

نمودار مسیر اثر مستقیم چیست؟

در نمودار مسیر اثر مستقیم یک متغیر اثر بلافصل و بی‌واسطه آن متغیر بر متغیر دیگری است که با پیکان نشان داده می‌شود و مقدار آن همان ضریب مسیر دو متغیر است. به عبارت دیگر ضریب مسیر p_ij مبین اثر مستقیم متغیرjام بر متغیر iام است.

تعریف 6: اثر مستقیم یک متغیر مستقل اثر بی‌واسطه آن بر متغیر وابسته است که همان ضریب مسیر دو متغیر است.

به عنوان مثال در نمودار مسیر شکل 7 ضریب مسیر P₃₁ که معادل 475/0 است اثر مستقیم متغیر مستقل X1 بر متغیر وابسته X3 است و ضریب مسیر P₃₂ که معادل 504/0 است اثر مستقیم متغیر مستقل X2 بر متغیر وابسته X3 است. همچنین ضریب مسیرP₂₁ که معادل 764/0 است اثر مستقیم متغیر برونزاد X1 بر متغیر مستقل درونزاد X2 است.

نمودار مسیر اثر غیر مستقیم چه کاربردی دارد؟

در نمودار مسیر اثر غیرمستقیم تأثیر متغیری بر متغیری دیگر از طریق متغیر یا متغیرهای رابط است. متغیر رابط هم متغیری است که هم متأثر از متغیر علت است و هم مؤثر بر متغیر معلول. مقدار اثر غیرمستقیم از ضرب کردن ضرایب مسیری که در آن مسیر غیرمستقیم قرار دارند به دست می‌آید.

به عنوان مثال در شکل 7 متغیر مستقل X1 از طریق متغیر مستقل X2 بر متغیر وابسته X3 اثر غیرمستقیم دارد. مقدار این اثر غیرمستقیم عبارت است از حاصل ضرب ضریب مسیر P₂₁ در ضریب مسیرP32:

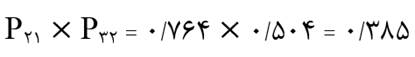
اما متغیر مستقل X2 بر متغیر وابسته X3 اثر غیرمستقیم ندارد. به عبارت دیگر اثر غیرمستقیم متغیر مستقل X2 بر متغیر وابسته X3 صفر است.

تعریف 7: اثر غیرمستقیم یک متغیر مستقل اثر آن بر متغیر وابسته از طریق متغیر یا متغیرهای رابطی است که بین آن دو قرار دارند.

اثر کاذب در نمودار مسیر چه کاربردی دارد؟

در نمودار مسیر اثر کاذب یک متغیر مستقل بخشی از اثر آن متغیر بر متغیر وابسته است که ناشی از تأثیر متغیر یا متغیرهای دیگر مدل بر هردو متغیر است.

به عنوان مثال در نمودار مسیر شکل 7 اثر کاذب متغیر مستقل X2 بر متغیر وابسته X3 بخشی از اثر متغیر مستقل X2 بر متغیر وابسته X3 است که ناشی از اثر متغیر مستقل X1 است چه هر دو متغیر X2 وX3 متأثر از آن متغیرند.

اما متغیر مستقل X1 اثر کاذبی بر متغیر وابسته X3 ندارد چه در آن نمودار مسیر هیچ متغیری وجود ندارد که هر دو متغیر متأثر از آن باشند. یک متغیر مستقل برونزاد فاقد اثر کاذب است زیرا طبق تعریف متغیر مستقل برونزاد در یک نمودار مسیر متغیری است که هیچ متغیری بر آن تأثیر ندارد.

تعریف 8: اثر کاذب یک متغیر بخشی از اثر یک متغیر علت بر متغیر معلول است که ناشی از تأثیر متغیر یا متغیرهای دیگر مدل بر هر دو متغیر است.

اثر کاذب متغیر مستقل بر متغیر وابسته از تجزیه اثر مرتبه صفر به سه اثر مستقیم و غیرمستقیم و کاذب به دست می‌آید:

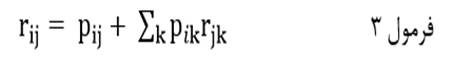
که درآن r_ij اثر مرتبه صفر متغیر مستقل X_j بر متغیر وابسته X_i است وp_ij ضریب مسیر متغیر مستقل X_j با متغیر وابسته X_i و p_ik ضریب مسیر متغیر وابسته X_i با متغیر مستقلی است که اثر مستقیمی بر متغیر مستقل X_j دارد و r_jk همبستگی متغیر مستقل X_j با متغیر مستقلی است که اثر مستقیمی بر آن دارد.

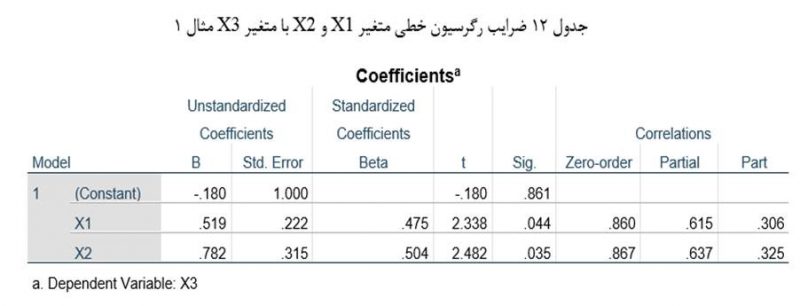
به عنوان مثال در نمودار مسیر شکل 7 برای احتساب اثر کاذب متغیر مستقل X2 بر متغیر وابسته X3 همبستگی مرتبه صفر آن دو متغیر را با توجه به ضرایب مسیر مقتضی در نمودار مسیر و همبستگی متغیرهای مدل (جدول 11) با فرمول 3 تجزیه می‌کنیم:

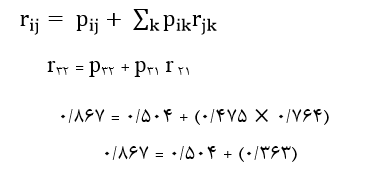
در این مثال اثر مستقیم X2 بر X3 (که همان ضریب مسیر آن دو متغیر است) 0/504 و اثر غیرمستقیم آن صفر است. بنابراین اثر کاذب X2 بر X3 معادل 0/363 است.

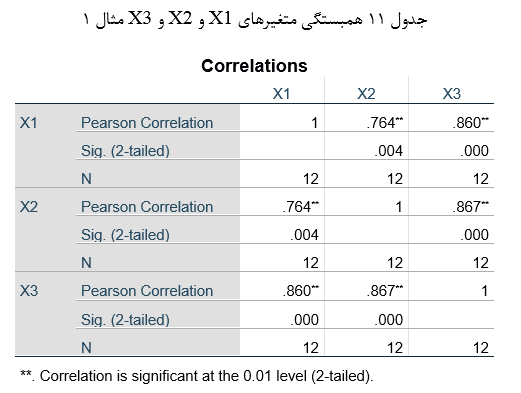
اثر کاذب متغیر مستقل بر متغیر وابسته را می‌توان به صورت ساده هم به دست آورد. از آنجا که همبستگی مرتبه صفر دو متغیر مجموع اثر مستقیم و اثر غیرمستقیم و اثر کاذب متغیر مستقل بر متغیر وابسته است (فرمول 3) در نتیجه اثر کاذب متغیر مستقل بر متغیر وابسته با نماد sr_ij عبارت است از:

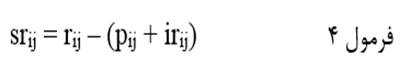
که در آن r_ij اثر مرتبه صفر متغیر مستقل X_j بر متغیر وابسته X_i است و p_ij اثر مستقیم متغیر X_j بر متغیر وابسته X_i و ir_ij اثر غیرمستقیم X_j بر X_i.

به عنوان مثال در نمودار مسیر شکل 7 که اثر مرتبه صفر متغیر مستقل X2 بر متغیر وابسته X3 معادل 0/637 (جدول 12) و اثر مستقیم X2 برX3 (که همان ضریب مسیر آن دو است) 0/504 است و متغیر مستقل X2 بر متغیر وابسته X3 اثر غیرمستقیمی ندارد (اثر غیرمستقیم X2 برX3 صفر است) اثر کاذب X2 بر X3  عبارت است از:

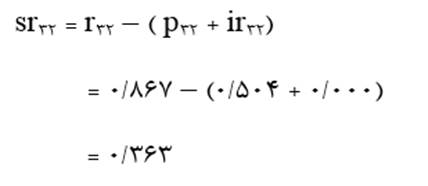
که معادل همان مقداری است که با فرمول 3 به دست آمد.

نکته 3: در نمودار مسیر متغیر مستقل برونزاد بر هیچ متغیری اثر کاذب ندارد.

نکته 4: در نمودار مسیر متغیر مستقل درونزاد بر متغیر وابسته اثر کاذب دارد.

اثر خالص در نمودار مسیر چه کاربردی دارد؟

در نمودار مسیر اثر خالص متغیر مستقل X_j بر متغیر وابسته X_i (با نماد pr_ij ) همبستگی دو متغیر بعد از حذف (کنترل) اثر متغیرهای مستقل مؤثر بر متغیر مستقل X_j از آن متغیر مستقل است.

احتساب اثر خالص متغیر مستقل به روابط بین متغیرهای مستقل نمودار مسیر بستگی دارد. برای احتساب اثر خالص متغیر مستقل X_j بر متغیر وابسته X_i از متغیر مستقل X_j به عنوان متغیر وابسته با متغیرهای مستقل دیگر که بر اساس نمودار مسیر بر آن متغیر مستقل مؤثرند رگرسیون خطی می‌گیریم و باقیمانده‌های آن را به صورت یک متغیر در نظرگرفته و بین آن متغیر باقیمانده و متغیر وابسته X_i همبستگی دو متغیره می‌گیریم.

تعریف 9: اثر خالص یک متغیر مستقل عبارت است از اثر آن بر متغیر وابسته بعد از برداشتن اثر سایر متغیرهای مؤثر برآن.

در واقع اثر خالص متغیر مستقل X_j بر متغیر وابسته X_i همان همبستگی نیمه جزیی دو متغیر است. از این رو اثر خالص متغیر مستقل X_j بر متغیر وابسته X_i را می‌توان با فرمان همبستگی جزیی و نیمه جزیی در رگرسیون خطی متغیر وابسته X_i با متغیر مستقل X_j و متغیرهای مستقل مؤثر بر متغیر مستقل X_j به دست آورد.

به عنوان مثال در نمودار مسیر شکل 7 اثر خالص متغیر مستقل X2 بر متغیر وابسته X3 اثر متغیر X2 بعد از برداشتن اثر متغیر مستقل X1 از روی آن است که همان همبستگی نیمه جزیی دو متغیرX2 و X3 با کنترل متغیر X1 است. همان‌طور که در جدول 12 آمده است این همبستگی نیمه جزیی 0/325 است. این بدان معناست که در نمودار مسیر مثال 1 (شکل7) اثر خالص متغیر مستقل X2 بر متغیر وابسته X2 معادل 0/325 است.

در نمودار مسیر اثر خالص متغیر مستقل برونزاد بر متغیر وابسته همان همبستگی مرتبه صفر آن است چه متغیر مستقل برونزاد در یک نمودار مسیر متغیری است که هیچ متغیری بر آن تأثیر ندارد. به عنوان مثال در نمودار مسیر شکل 7 اثر خالص متغیر مستقل برونزاد X1 بر متغیر وابسته X3 همان همبستگی مرتبه صفر آن است که معادل 0/860 است (جدول 12).

کاربرد مجذور اثر خالص در نمودار مسیر چیست ؟

در نمودار مسیر مجذور اثر خالص یک متغیر مستقل نسبتی از تغییر متغیر وابسته است که آن متغیر مستقل به تنهایی تبیین می‌کند و اگر قائل به رابطه علی بین آن دو باشیم نسبتی از تغییر متغیر وابسته است که ناشی از آن متغیر مستقل است.

مجموع مجذور اثر خالص متغیرهای مستقل هم نسبتی از تغییر متغیر وابسته است که مجموعه متغیرهای مستقل نمودار مسیر تبیین می‌کند. از این رو مجموع مجذور اثر خالص متغیرهای مستقل معادل ضریب تعیین (R² ) نمودار مسیر است که مبین نسبتی از تغییر متغیر وابسته است که مجموعه متغیرهای مستقل تبیین می‌کند:

که در آن pr_ij اثر خالص متغیر مستقل X_j بر متغیر وابسته X_i است.

به عنوان مثال در نمودار مسیر شکل 7 که اثر خالص متغیر مستقل X2 بر متغیر وابسته X3 معادل 0/325 و اثر خالص متغیر مستقل X1 معادل 0/860 است ضریب تعیین عبارت است از:

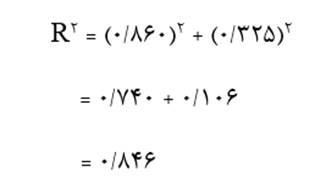
که معادل مقدار ضریب تعیین رگرسیون خطی متغیر X3 با متغیرهای X1 و X2 است (جدول 9).

کاربرد اثرات متغیرهای مستقل در تحلیل مسیر

در تحلیل مسیر تعیین اثرات مختلف تک تک متغیرهای مستقل اساساً برای مقایسه تأثیر متغیرهای مستقل بر متغیر وابسته از جوانب گوناگون است. با مقایسه اثرات مستقیم معلوم می‌شود کدام متغیر مستقل بیشترین یا کمترین اثر مستقیم را بر متغیر وابسته دارد. یا با مقایسه اثرات غیرمستقیم مشخص می‌شود کدام متغیر مستقل بیشترین یا کمترین اثر غیرمستقیم را بر متغیر وابسته دارد. یا کدام متغیر مستقل بیشترین یا کمترین اثر کاذب را دارد.

اما از همه مهمتر مقایسه اثرات خالص است که نشان می‌دهد هر متغیر مستقل نمودار مسیر چه نقشی در متغیر وابسته دارد. به ویژه مجذور اثرات خالص حائز اهمیت است که نشان می‌دهد هر متغیر مستقلی چه نسبتی از تغییر وابسته را تبیین می‌کند.

برای تسهیل مقایسه اثرات مختلف یک متغیر مستقل و مقایسه اثرات مختلف متغیرهای مستقل همه اثرات مختلف متغیرهای مستقل یک نمودار مسیر را در جدولی تحت عنوان ماتریس اثرات ارائه می‌کنیم.

ماتریس اثرات چیست؟

ماتریس اثراتجدولی است شامل تمام اثرات متغیرهای مستقل یک نمودار مسیر (مانند جدول 13) که برای مقایسه اثرات مختلف متغیرهای نمودار مسیر به کار می‌رود.

در ستون اول ماتریس اثرات نام متغیرهای مستقل نمودار مسیر درج می‌شود. ستون دوم به همبستگی متغیرهای مستقل با متغیر وابسته اختصاص دارد که همان اثر مرتبه صفر متغیرهای مستقل است و از سه جزء (اثر مستقیم و اثرغیرمستقیم و اثر کاذب) تشکیل شده است. اثر مستقیم در ستون سوم می‌آید که اثر بلافصل متغیر مستقل بر متغیر وابسته است. اثر غیرمستقیم که اثر متغیر مستقل بر متغیر وابسته از طریق متغیر یا متغیرهای دیگر است در ستون چهارم می‌آید. اثر کاذب هم که بخشی از اثر متغیرمستقل بر متغیر وابسته است که ناشی از تأثیر متغیر یا متغیرهای دیگر مدل بر هر دو متغیر است در ستون بعدی می‌آید.

ستون ششم ماتریس اثرات به اثر خالص متغیرهای مستقل بر متغیر وابسته اختصاص دارد که همبستگی هر متغیر مستقل با متغیر وابسته بعد از برداشتن اثر متغیرهای مستقل مؤثر بر آن متغیر مستقل از روی آن متغیر مستقل است. ستون آخر هم مجذور اثر خالص متغیرهای مستقل است که مبین نسبتی از تغییر متغیر وابسته است که هر یک از متغیرهای مستقل تبیین می‌کند.

با تهیه ماتریس اثرات با سهولت می‌توان به ارزیابی و مقایسه اثرات مختلف متغیرهای مستقل پرداخت. به عنوان مثال در ماتریس اثرات نمودار مسیر شکل 7 (جدول 13) می‌بینیم همبستگی مرتبه صفر و اثر مستقیم متغیر مستقل X2 اندکی بیشتر از متغیر مستقل X1 است. اما متغیر مستقل X1 اثر غیرمستقیمی بر متغیر وابسته دارد در حالی که متغیر مستقل X2 اثر غیرمستقیم ندارد. در عوض X2 دارای اثر کاذب بر متغیر وابسته است در حالی که متغیر مستقل X1 اثر کاذب ندارد.

مقایسه اثرات خالص نشان می‌دهد اثر خالص متغیر مستقل X1 بر متغیر وابسته به مراتب بیشتر از اثر خالص متغیر مستقل X2 است. مجذور اثر خالص متغیر مستقل X1 بر متغیر وابسته که 0/740 است حدود هفت برابر مجذور اثر خالص متغیر مستقل X2 است که فقط 0/106 است. این بدان معناست که سهم متغیر مستقل X1 در تبیین متغیر وابسته حدود هفت برابر سهم متغیر مستقل X2 است.

مثال 4: در این مثال تمام مراحل یک تحلیل مسیر 4 متغیره را انجام می‌دهیم. فرض کنیم محققی بر اساس چارچوبی نظری استدلال می‌کند سه متغیر جنسیت و تحصیلات و سمت اداری سه عامل عمده درآمد کارکنان حقوق‌بگیر است.

استدلال وی به طور خلاصه به این شرح است: در جوامع معاصر عموماً جایگاه مردان بالاتر از زنان است و از این رو به طور متوسط درآمد مردان از زنان بیشتر است. تحصیلات هم بیانگر تخصص است و تقسیم کار در جوامع معاصر هم مبتنی بر تخصص است. بنابراین درآمد رابطه مستقیمی با تحصیلات دارد: هر چه تحصیلات بیشتر درآمد بیشتر. سمت اداری هم جایگاهی در سلسله مراتب اداری است و طبعاً رابطه مستقیمی با درآمد دارد (هر چه سمت اداری بالاتر درآمد بیشتر).

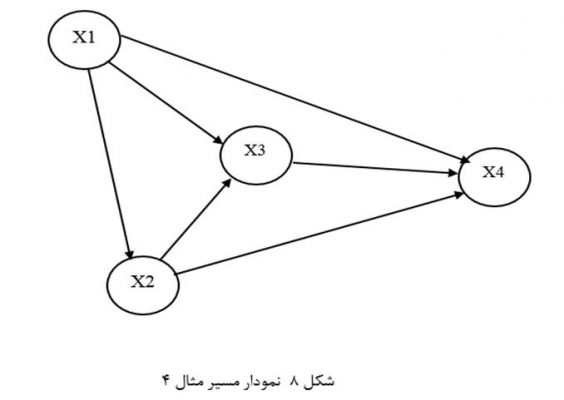
همچنین سمت‌های اداری به همان دلیل بالا بودن جایگاه مردان و اهمیت تخصص عموماً به مردان و افراد دارای تحصیلات بالاتر اختصاص می‌یابد. به عبارت دیگر جنسیت و تحصیلات بر سمت اداری تأثیر دارد. و باز به دلیل بالا بودن جایگاه مردان به طور متوسط تحصیلات مردان بالاتر است. به عبارت دیگر جنسیت بر تحصیلات هم تأثیر دارند. مجموعه این روابط بین چهار متغیر به صورت نمودار مسیر شکل 8 ترسیم شده است.

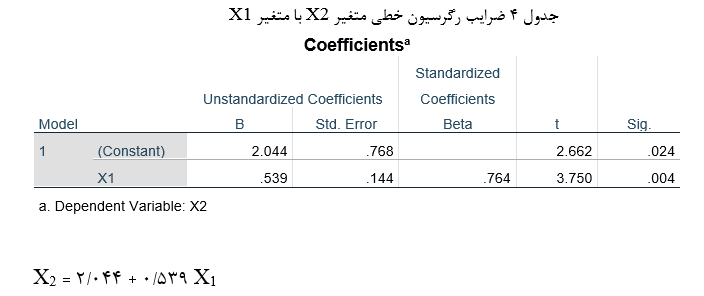
گیریم داده‌های مقتضی برای سنجش متغیرهای نمودار مسیر شکل 8 و آزمون مدل را از نمونه‌ای احتمالی از جمعیتی معین (کارکنان شرکت بزرگ الف) گرد آورده‌ایم (جدول 14). جنسیت (X1) متغیری دوشقی و به صورت صفر و 1 کدگذاری شده (صفر برای زن و 1 برای مرد) و تحصیلات (X2) متغیری کمی بر حسب سال و سمت اداری (X3) از پایین‌ترین تا بالاترین سطح به صورت متغیری کمی از صفر تا 4 و درآمد ماهانه (X3) متغیری کمی بر حسب هزار تومان اندازه‌گیری و وارد فایل SPSS شده است.

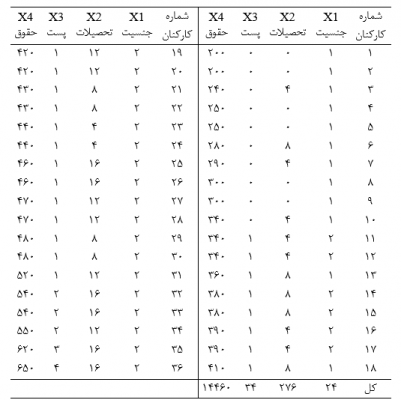
حال برای تحلیل مسیر مدل مذکور در مرحله اول به وارسی مفروضات می‌پردازیم. همان‌طور که به میان آمد جنسیت (X1) متغیری دوشقی و تحصیلات(X2)  و سمت اداری (X3) هم به صورت متغیری کمی اندازه‌گیری شده‌اند (فرض اول). در شکل 9 الی 11 نیز می‌بینیم روابط متغیرهای معلول با متغیرهای علت خطی است (فرض دوم) و جمع‌پذیری روابط را نیز مفروض می‌گیریم.

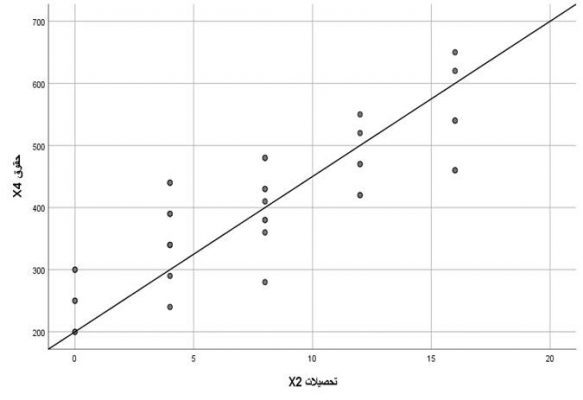
شکل 9 نمودار پراکنش X4 بر حسب X2 مثال 4

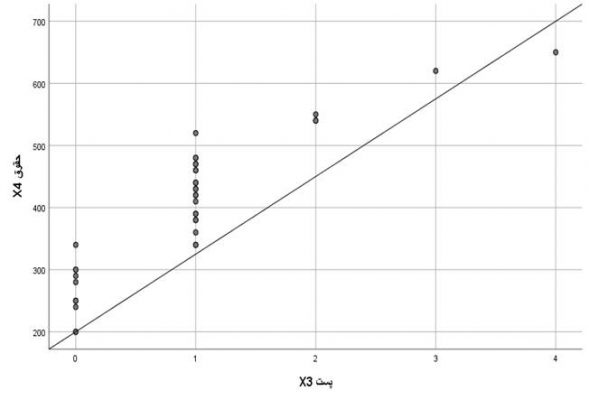
شکل 10 نمودار پراکنش X4 بر حسب X3 مثال 4

فرض یکطرفه‌بودن جریان علت در متغیرها نیز مبتنی بر استدلال نظری محقق است (فرض سوم) و همان‌طور که در جدول 15 می‌بینیم همبستگی E4 (باقیمانده X4 ) با E3 (باقیمانده X3 ) و با E2 (باقیمانده X2 ) و همبستگی E3 با E2 همگی صفرند (فرض چهارم).

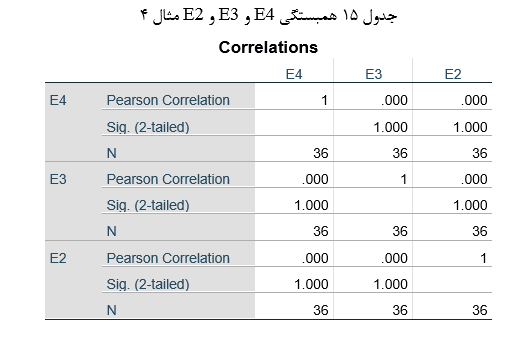
حال با حصول اطمینان از مفروضات تحلیل مسیر در مرحله دوم به تحلیل رگرسیون خطی مقتضی می‌پردازیم.

تحلیل مسیر مثال 4 مستلزم سه معادله رگرسیون خطی است. اول رگرسیون خطی متغیر وابسته X4 با سه متغیر X1 و X2 و X3 :

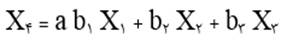
دوم رگرسیون خطی متغیر مستقل درونزاد X3 با متغیر مستقل X1 و X2 :

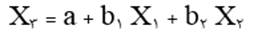
سوم رگرسیون خطی متغیر مستقل درونزاد X2 با متغیر مستقل X1 :

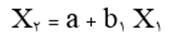
تحلیل رگرسیون خطی متغیر وابسته درآمد ماهانه (X4) با سه متغیر مستقل جنسیت (X1) و تحصیلات (X2) و سمت اداری (X3) نشان می‌دهد هر سه متغیر مستقل دارای رابطه معناداری با متغیر وابسته‌اند. (جدول 16).

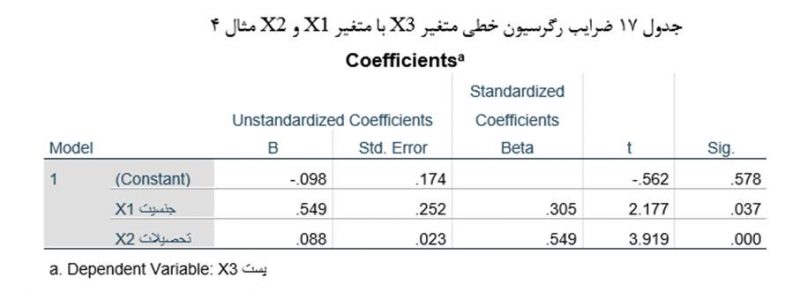
تحلیل رگرسیون خطی متغیردرونزاد سمت اداری (X3) با دو متغیر مستقل جنسیت (X1) و تحصیلات (X2) نیز نشان می‌دهد هر دو متغیر مستقل رابطه معناداری با آن متغیر دارند (جدول 17).

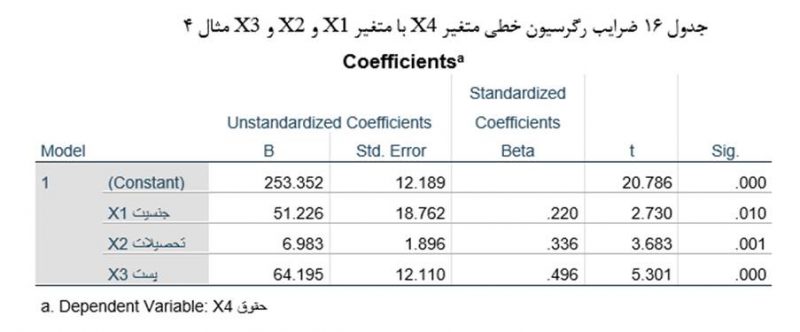
همچنین تحلیل رگرسیون خطی متغیر درونزاد تحصیلات (X2) با متغیر مستقل جنسیت (X1) نشان می‌دهد متغیر مستقل جنسیت رابطه معناداری با آن متغیر دارد (جدول 18).

تأیید همه مفروضات نمودار مسیر شکل 8 مبین برازندگی مدل در آن جمعیت (انطباق مدل با واقعیت) است (مرحله سوم).

شاخص این برازندگی هم ضریب تعیین رگرسیون خطی متغیر وابسته با متغیرهای مستقل نمودار مسیر است. همان‌طور که در جدول 19 می‌بینیم مقدار ضریب تعیین تعدیل‌یاقته آن مدل حدود 0/89 است. این بدان معناست اگر همان‌طور که محقق استدلال کرده بین متغیرها روابط علی وجود داشته باشد 0/89 از تغییر متغیر وابسته درآمد ماهانه (X4) کارکنان شرکت بزرگ الف ناشی از سه متغیر مستقل جنسیت (X1) و تحصیلات (X2) و سمت اداری (X3) آنهاست.

از آنجایی که نمودار مسیر شکل 8 دارای برازندگی در جمعیت مورد آزمون است ضرایب مسیر متغیرها را از روی تحلیل رگرسیون مقتضی (جدول 16 الی 18) و ضرایب مسیر باقیمانده‌ها را از روی ضریب تعیین‌های مقتضی (جدول 19 الی 21) احتساب کرده و وارد نمودار مسیر می‌کنیم (شکل 12).

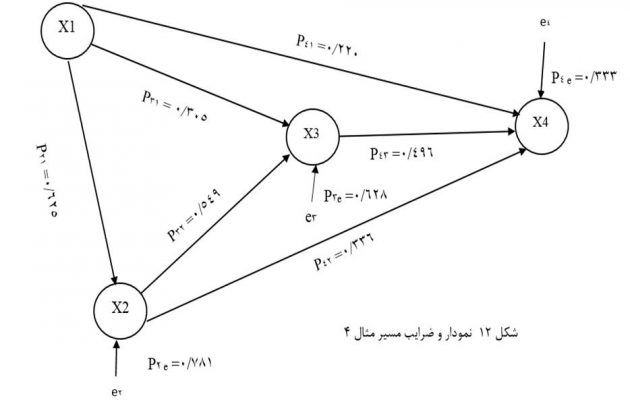
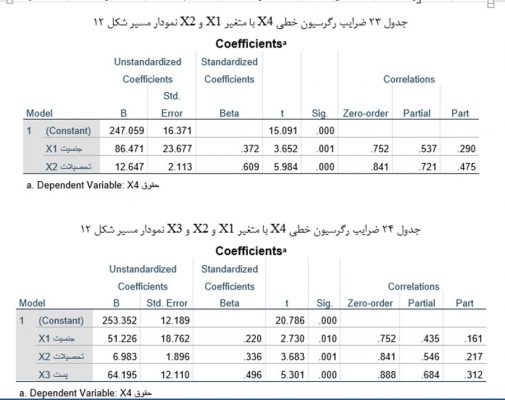
حال برای ارزیابی و مقایسه اثرات مختلف متغیرهای مستقل ماتریس اثرات نمودار مسیر شکل 12 را تشکیل می‌دهیم (جدول 22). همبستگی مرتبه صفر متغیرهای مستقل با متغیر وابسته را از جدول ضرایب رگرسیون خطی X4 با X1 و X2 و X3 (جدول 24) و اثر مستقیم متغیرهای مستقل بر متغیر وابسته را نیز از ضرایب مسیر شکل 12 استخراج می‌کنیم.

اثر غیرمستقیم متغیر مستقل جنسیت (X1) بر متغیر وابسته درآمد ماهانه (X4) شامل اثر X1 از طریق متغیر X2 به X4 و از طریق X3 به X4 و همچنین از طریق X2 به X3 به X4 است. اثر غیرمستقیم متغیر مستقل تحصیلات (X2) بر متغیر وابسته درآمد ماهانه (X4) شامل اثر X2 از طریق X3 به X4 است. متغیر مستقل سمت اداری (X3) هم اثر غیرمستقیمی برمتغیر وابسته (X4) ندارد.

جنسیت (X1) که متغیر مستقل برونزاد است بر متغیر وابسته درآمد ماهانه (X4) اثر کاذب ندارد. اما متغیر مستقل درونزاد تحصیلات (X2) بر متغیر وابسته درآمد ماهانه (X4) اثر کاذب دارد که ناشی از تأثیر متغیر جنسیت (X1) بر هر دو متغیر است. این اثر کاذب طبق فرمول 4 از کم کردن مقدار اثر مستقیم و غیرمستقیم X2 از همبستگی مرتبه صفر آن با متغیر وابسته درآمد ماهانه (X4) به دست می‌آید:

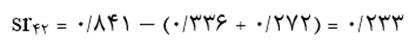
متغیر مستقل درونزاد سمت اداری (X3) هم بر متغیر وابسته درآمد ماهانه (X4) اثر کاذب دارد که ناشی از تأثیر متغیر جنسیت (X1) و تحصیلات (X2) بر هر دو متغیر است. این اثر کاذب هم از کم کردن مقدار اثر مستقیم و غیرمستقیم X3 از همبستگی مرتبه صفر آن با متغیر وابسته درآمد ماهانه (X4) احتساب می‌شود:

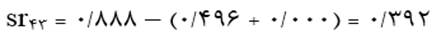
اثر خالص متغیر مستقل جنسیت برونزاد (X1) برمتغیر وابسته درآمد ماهانه (X4) معادل همبستگی مرتبه صفر آن است. اثر خالص متغیر مستقل درونزاد تحصیلات (X2) بر متغیر وابسته درآمد ماهانه (X4) همبستگی نیمه جزیی آن دو با حذف اثر X1 بر X2 است. این همبستگی با فرمان همبستگی جزیی و نیمه جزیی در رگرسیون خطی متغیر وابسته X4 با دو متغیر مستقل X1 و X2 به دست می‌ آید (جدول 23) که معادل 0/475 است.

اثر خالص متغیر مستقل درونزاد سمت اداری (X3) بر متغیر وابسته درآمد ماهانه (X4) همبستگی نیمه جزیی آن دو با حذف اثر X1 و X2 برX3 است. این همبستگی با فرمان همبستگی جزیی و نیمه جزیی در رگرسیون خطی متغیر وابسته X4 با سه متغیر مستقل X1 و X2 وX3 به دست می‌آید. (جدول 24) که معادل 0/312 است.

حال در ارزیابی و مقایسه اثرات مختلف متغیرهای مستقل (جدول 22) می‌بینیم همبستگی مرتبه صفر و اثر مستقیم متغیر مستقل سمت اداری (X3) بیشتر از متغیر مستقل جنسیت (X1) و تحصیلات (X2) است. در عوض متغیر مستقل جنسیت (X1) دارای بالاترین اثر غیرمستقیم بر متغیر وابسته است و اثر غیرمستقیم تحصیلات (X2) در مرتبه بعدی قرار دارد و متغیر مستقل سمت اداری (X3) اثر غیرمستقیم ندارد.

همچنین سمت اداری (X3) دارای بالاترین اثر کاذب بر متغیر وابسته درآمد ماهانه (X4) است. اثر کاذب تحصیلات (X2) در مرتبه بعدی قرار دارد و متغیر مستقل جنسیت (X1) اثر کاذبی ندارد.

از همین رو اثر خالص متغیر مستقل جنسیت (X1) بر متغیر وابسته درآمد ماهانه (X4) به مراتب بیشتر از اثر خالص متغیر تحصیلات (X2) و به ویژه سمت اداری (X3) است. مجذور اثر خالص متغیر X1 بر متغیر وابسته X4 که 0/565 است حدود 2/5 برابر مجذور اثر خالص متغیرX2 است که فقط 0/227 است و حدود 6 برابر مجذور اثر خالص متغیر X3 است که فقط 0/097 است. این بدان معناست که سهم جنسیت در تبیین تغییر درآمد ماهانه حدود 2/5 برابر سهم تحصیلات و 6 برابر سهم سمت اداری است.

در این مطلب سعی کردیم با مثال های کاربردی مفهوم تحلیل مسیر و کاربرد های مهم آن را برای شما شرح دهیم. امیدواریم که از این مطلب به خوبی استفاده کنید. چنانچه درباره تحلیل مسیر سوالی داشتید در زیر این پست کامن بگذارید تا کارشناسان سایت به شما پاسخ دهند. چنانچه سوالی با توجه به پروژه مخصوص خود دارید می توانید باتکمیل فرم در قسمت مشاوره آماری رایگان با افراد متخصص و با تجربه ارتباط برقرار نمایید.

همچنین اگر علاقه مند به مباحث آماری هستید برای با خبر شدن از جدید ترین مطالبی که بر روی سایت آمار پیشرو قرار می گیرد، می توانید صفحه اینستاگرام آمار پیشرو را دنبال کنید. اگر نیاز به انجام پروژه های اماری دارید و چنانچه خیلی نمی خواهید وقت خود را از دست دهید، با رفتن به بخش ثبت سفارش فرم را تکمیل کرده تا کارشناسان در سریعترین زمان ممکن با شما تماس بگیرند و پروژه شما را آغاز کنند.