طرح آزمایشات کاملا تصادفی +جدول تجزیه واریانس

[block id=”breadcrumb”]

طرح آزمایشات یکی از مباحث تخصصی آماری است که آن را در بخش های عملیاتی که برای آزمایش اجرا می شود. طرح آزمایشات کشاورزی یکی از مهم ترین مباحث در  این طرح ها است. در این مطلب ابتدا تعریف هایی را ارائه می دهیم و سپس به روشی کاملا کاربردی مراحل آن را اجرا می کنیم.در انتها 3 نوع از پر کاربرد ترین طرح ها را به صورت تفصیلی توضیح می دهیم.

طرح آزمایشات چیست؟

طرح آزمایشات الگوهای ابداع شده‌ای هستند که برای انجام آزمایشات مقایسه‌ای مورد استفاده قرار می‌گیرند. آزمایش در اینجا به کلیه عملیاتی اطلاق می‌شود که برای رد یا قبول یا تکمیل فرضیه‌ای بکار می‌روند. وجه تمایز یک آزمایش مقایسه‌ای و یک آزمایش مطلق در این است که در آزمایش مقایسه‌ای دو یا چند مورد مقایسه می‌شوند، در حالی که در آزمایش مطلق، بررسی فقط روی یک ماده (مثلا یک واکنش شیمیایی) انجام می‌گیرد. طرح آزمایشات اغلب از آزمایش‌های مقایسه‌ای صحبت می‌شود که نمونه‌ای از آن در مثال زیر آورده شده است. آزمایش مقایسه عملکرد چهار واریته ذرت (A، B،  Cو D) را در نظر بگیرید:

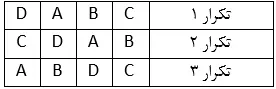
تیمار (Treatment)

در طرح آزمایشات هر یک از عواملی را که برای مطالعه اثر آن‌ها بر روی یک صفت یا صفات مختلف در یک آزمایش مورد مقایسه قرار می‌گیرند تیمار می‌گویند. مثلا اگر مقادیر مختلف کود بر روی عملکرد ذرت مقایسه شوند هر مقدار کود یک تیمار است. در مثال بالا هر واریته ذرت یک تیمار است. در مثال دیگر فرض کنید می‌خواهیم ببینیم که آیا انواع مختلف لاستیک (A، B،  Cو D) از نظر میزان ساییدگی بعد از طی مسافت 20000 مایل با هم تفاوت دارند یا نه؟. در این مثال نوع لاستیک تیمار است.

در طرح آزمایشات کشاورزی زمان‌های مختلف آبیاری، فاصله ردیف‌های کشت، سموم حشره کش و رژیم‌های غذایی دام و غیره می‌توانند به عنوان تیمار  وارد شوند. بدیهی است که تیمار محدود به کشاورزی نیست و در هر نوع پژوهش علمی اعم از زیستی، دامپزشکی، یا پزشکی به کار می‎‌رود.

ماده آزمایشی (Experimental material)

مقایسه تیمارها در طرح آزمایشات به کمک وسیله یا موجودی انجام می‌گیرد. موجود یا وسیله مورد نظر را ماده آزمایشی می‌نامند. مثلا برای مقایسه چند واریته ذرت بایستی آن‌ها در مزرعه‌ای کاشته شوند. خاک در اینجا ماده آزمایشی می‌باشد. برای مقایسه اثر چند نوع رژیم غذایی در یک نژاد دام، ماده آزمایشی نژاد دام خواهد بود.

واحد آزمایشی (کرت یا پلات)

واحد آزمایشی کوچکترین قسمت از ماده آزمایشی است که در آن یک تیمار در یک تکرار تحت آزمایش قرار دارد. لغت کرت (پلات) در آزمایشات مزرعه‌ای به عنوان واحد آزمایشی به کار می‌رود. در آزمایش‌های دامی، یک راس دام یا مجموعه‌ی چند دام می‌تواند یک واحد آزمایشی تلقی شود.

بلوک

به گروهی از واحدهای آزمایشی با تیمارهای مختلف که تحت شرایط مشابهی تشکیل شده باشد بلوک اطلاق می‌شود. اگر در گروه مربوط به بلوک، کلیه تیمارهای مورد آزمایش وجود داشته باشند آن را بلوک کامل و اگر در تشکیل بلوک فقط عده‌ای از تیمارها شرکت داشته باشند آن را بلوک ناقص می‌نامند.

در آزمایش مقایسه ساییدگی انواع لاستیک‌ها بلوک می‌تواند نوع خودرو، موقعیت قرار گرفتن لاستیک‌ها روی خودرو یا نوع راننده باشد. هر عملیاتی در مورد تیمارهای متعلق به یک بلوک باید به صورت مشابه انجام گیرد. به عنوان مثال زمینی که یک بلوک اشغال می‌کند باید حداکثر یکنواختی ممکن را داشته باشد. برای توضیح بیشتر لازم است آزمایش مقایسه ساییدگی انواع لاستیک‌ها را بیشتر تشریح کنیم:

فرض کنید در این آزمایش موقعیت قرارگیری لاستیک‌ها (جلو راست، جلو چپ، عقب راست و عقب چپ) به عنوان بلوک و نوع لاستیک (A، B،  Cو D) به عنوان تیمار در نظر گرفته شود.

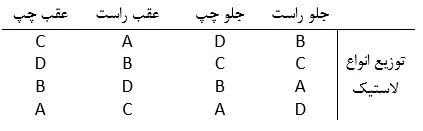
همان‌طور که در طرح فوق مشاهده می‌شود واحدهای مورد آزمایش ما در سطح هر بلوک به صورت تصادفی پخش شده‌اند. در واقع تمام تیمارها در هر بلوک فقط یک‌بار مشاهده شده‌اند.

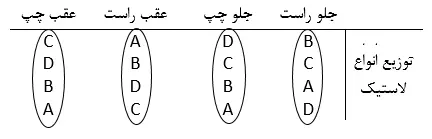
چنانچه بلوک را در نظر نگیریم و به صورت ردیفی به چینش تیمارها نگاه کنیم می‌بینیم که انواع مختلف لاستیک به صورت کاملا تصادفی پخش نشده‌اند و به عنوان مثال در ردیف دوم لاستیک نوع C دو بار در موقعیت‌های جلو راست و جلو چپ تکرار شده است. در واقع بلوک محدودیت در تصادفی کردن ماست و واحدهای مورد آزمایش حتما باید داخل هر سطح از بلوک به صورت تصادفی پخش شوند نه هر سطح از تیمار. همچنین محدودیت در مقایسه داریم.

یعنی حق نداریم هر مشاهده‌ای را یا هر سطح تیماری را با سطح تیمار دیگری از 2 سطح متفاوت از بلوک‌ها مقایسه کنیم. مثلا لاستیکی که در جلوی ماشین (راست یا چپ) قرار گرفته نسبت به لاستیکی که در عقب ماشین (راست یا چپ) قرار گرفته، قطعا میزان ساییدگی بیشتری دارد. بنابراین اگر بخواهیم لاستیک نوع A و نوع B را با هم مقایسه کنیم، باید هر دو در یک موقعیت (بلوک) باشند.

انواع تغییرات طرح آزمایشات

پیش از اجرای یک آزمایش باید طرحی تهیه گردد. در این طرح نه فقط تیمارها یا روش‌های مشاهده و اندازه‌گیری مورد توجه قرار می‌گیرند بلکه نکاتی نیز رعایت می‌شوند که بدون آن‌ نتایج حاصله نامفهوم خواهند بود و چه بسا این نتایج، مربوط به عوامل نامعلومی باشند و به تیمارها نسبت داده شوند. به طور کلی یک طرح آزمایشی خوب طرحی است که در آن بتوان دو نوع تغییرات یا پراکندگی زیر را از هم تفکیک کرد:

1. تغییرات قابل کنترل یا سیستماتیک
2. تغییرات غیر قابل کنترل یا تصادفی

عوامل قابل کنترل که منجر به تغییرات قابل کنترل می‌شوند عبارتند از:

• عواملی که مطالعه آن‌ها هدف آزمایش است مانند تیمارها
• عواملی شناخته شده دیگری که می‌توانند روی نتایج تاثیر داشته باشند، ولی طوری در آزمایش کنترل می‌گردند که بتوان اثر آن‌ها را به هنگام قضاوت در روی نتایج محاسبه کرد مانند بلوک.

عوامل غیرقابل کنترلی که تغییرات تصادفی از آن‌ها ناشی می‌گردند به عوامل تصادفی موسوم هستند. این تغییرات از 3 دسته زیر تشکیل می‌شوند:

• تغییرات مربوط به محیط مثل عوامل آب و هوایی، عوامل مرتبط با خاک و موجودات خاکزی
• تغییرات مربوط به موجود زنده مثل صفات فیزیولوژیک، مرفولوژیک و شیمیایی که عملکرد و کیفیت محصول نبات یا دام به آن‌ها بستگی دارد و نوسانات زیادی را نشان می‌دهند.
• تغییرات مربوط به مجریان طرح مانند مجری مبتدی یا بی‌طرف نبودن مجری

این عوامل نمونه‌ای از عوامل غیرقابل کنترل هستند که خطای آزمایشی از این قبیل عوامل ناشی می‌شوند.

خطای آزمایشی و جلوگیری از آن در طرح آزمایشات

از مطالعه بندهای فوق نتیجه می‌گیریم که هر آزمایش باید با کمال دقت طراحی و اجرا شود تا نتایج حاصل از آن معتبر باشد. لکن هر قدر آزمایش با دقت و مراقبت صحیح انجام گیرد باز هم پراکندگی‌هایی وجود خواهند داشت که به علت عدم تساوی اثر عوامل غیر قابل کنترل در واحدهای آزمایشی پیدا شده‌اند. این پراکندگی‌ها را خطای آزمایشی می‌گویند. بایستی سعی گردد در حد امکان از مقدار خطاها کاسته شود تا دقت و حساسیت آزمایش بیشتر باشد. یکی از ارکان مهمی که می تواند خطای آزمایش را کم کند طرح آزمایشات است. خطای یک آزمایش بایستی دارای توزیع نرمال با میانگین صفر و واریانس ثابت باشد. برای کاهش خطای آزمایشی می‌توان از راه‌های زیر استفاده کرد:

• مواد آزمایشی همگن یا مشابه انتخاب شود.
• تکرارهای آزمایش متناسب اختیار شوند. تکرار بدین معنی است که یک تیمار چند بار تکرار بشود و نقش آن عبارت است از برآورد خطای آزمایشی و مقایسه هر چه دقیق‌تر اثر تیمارها. اصولا دقت یک آزمایش، بنا به عقیده اکثر مولفین و محققین، به تعداد تکرار بستگی دارد. هر قدر تعداد تکرار زیادتر باشد دقت آزمایش بیشتر می‌شود ولی در هر آزمایش حد متوسطی برای تعداد تکرار وجود دارد که اگر از این حد تجاوز نماید دقت آزمایش نه تنها به همان اندازه افزایش نمی‌یابد بلکه اضافه نمودن تکرار سبب افزایش هزینه و غیریکنواختی ماده آزمایشی و به طور غیرمستقیم زیاد شدن خطای آزمایشی می‌گردد. به تجربه ثابت شده است که در اکثر طرح‌های آزمایشی تعداد تکرار بسته به حساسیت آزمایش بین 4 تا 8 انتخاب می‌شود. یعنی در صورت حساس بودن آزمایش تعداد تکرار را تا 8 افزایش و با کاهش حساسیت آزمایش تکرار را تا 4 تقلیل می‌دهند.
• طرح مناسب به کار برده شود. انتخاب طرح‌هایی مناسب که بتوان منابع تغییر را در آن‌ها کنترل کرد. یک طرح باید طوری انتخاب شود که آزمایش با مشکلات اجرایی اغراق آمیز از جمله تکرار بیش از حد مواجه نشود که این خود می‌تواند خطای آزمایشی را بزرگ کند و مهم‌تر این‌که طرح امکان دهد تا برآورد صحیحی از خطای آزمایشی به‌دست آید. در طرح‌های بلوک‌دار با ایجاد محدودیت در تصادفی کردن، اغلب خطای آزمایشی کاهش می‌یابد.

انواع طرح‌ آزمایشات پایه

به‌طور کلی طرح‌های آزمایشی را می‌توان به دو دسته تقسیم کرد:

1. طرح‌هایی که در آن‌ها فقط اثر یک منبع پراکندگی مورد بررسی است. در این دسته تنها یک طرح وجود دارد و آن طرح “کاملا تصادفی شده” می‌باشد.
2. طرح‌هایی که در آن‌ها بیش از یک منبع پراکندگی مورد بررسی است. طرح‌های زیادی در این دسته قرار می‌گیرند که مهمترین آن‌ها طرح‌های “بلوکی کاملا تصادفی شده” و “مربع لاتین” هستند.

این 2 طرح پایه و اساس طرح آزمایشات را تشکیل می‌دهند و بقیه طرح‌ها به طور مستقیم یا غیرمستقیم از این 2 طرح منشاء می‌گیرند. انتخاب یکی از این 2 طرح پایه یا اصلی برای انجام یک آزمایش با توجه به نکات زیر انجام می‌گیرد:

• تعداد و نوع تیمار
• تعداد تکرار (میزان دقت آزمایش)
• کیفیت غیریکنواختی یا یکنواختی ماده آزمایشی

طرح آزمایشات کاملا تصادفی شده

همان‌طور که از اسم طرح پیداست، تیمارها به طور کاملا تصادفی در کرت‌ها یا واحدهای آزمایشی قرار می‌گیرند به طوری که هر یک از کرت‌ها شانس مساوی برای دریافت هر یک از تیمارها دارند. این طرح موقعی مورد استفاده قرار می‌گیرد که واحدهای آزمایشی یکنواخت باشند. بدین جهت برای آزمایش‌های گلخانه‌ای و آزمایشگاهی و اطاق‌های رشد خیلی مناسب است، چون در آن‌ها اثرات محیط می‌تواند یکنواخت باشد. اما در آزمایشات مزرعه‌ای به علت عدم یکنواختی قطعات مختلف خاک چندان قابل استفاده نیست.

یکی از خصوصیات این طرح آزمایشات قابل انعطاف بودن آن است یعنی محقق می‌تواند هر تعداد تیمار و برای هر تیمار هر تعداد تکرار را انتخاب نماید در صورتی که در دو طرح اصلی دیگر، تکرارهای مساوی برای تیمارهای مختلف لازم است. اگر تعداد تکرار برای تمام تیمارها یکسان باشد طرح را “متعادل” و در غیر این صورت طرح را “نامتعادل” می‌نامند.

همچنین از بین رفتن یک یا چند واحد آزمایشی، حتی یک تیمار، تجزیه آماری را با مشکل مواجه نمی‌سازد. مهمترین عیب این طرح آن است که دقت آن بخصوص در آزمایش‌های بزرگ زیاد نیست یعنی خطای آزمایشی در اینجا شامل همه منابع تغییر بین واحدها می‌شود به جز پراکندگی مربوط به اثرات تیمارها. بنابراین خطای آزمایشی غالبا بزرگ است. لازم است بار دیگر آزمایش مقایسه ساییدگی انواع لاستیک‌ها را در نظر بگیریم:

چنانچه 16 لاستیک از 4 نوع A، B،  Cو D را به صورت کاملا تصادفی و بی توجه به نوع خودرو روی 4 خودرو نصب کنیم و از طرح کاملا تصادفی شده استفاده کنیم متوسط آن مقدار ساییدگی لاستیک را که مربوط به خودروهاست و می‌تواند در نتیجه اثر بگذارد را حذف کرده‌ایم.

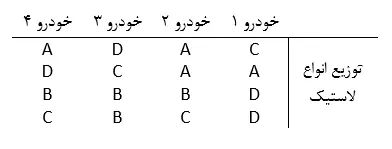
در این طرح خطای آزمایشی صرفا خطای تصادفی نیست و می‌تواند ناشی از تغییرات بین خودروها هم باشد. همان‌طور که می‌بینید مثلا لاستیک نوع B هیچ‌گاه روی خودروی اول نصب نشده است و یا لاستیک نوع A روی خودرو سوم امتحان نشده است. بنابراین طرحی لازم است که در آن هر نوع لاستیک یک‌بار روی هر نوع خودرو امتحان شود.

مدل ریاضی طرح کاملا تصادفی شده به این صورت است که فقط یک عامل پراکندگی یعنی اثر تیمارها کنترل می‌شود لذا تغییرات کل به دو قسمت مربوط به اثر تیمار و خطای آزمایشی تقسیم خواهد شد. این وضعیت با یک فرمول ساده ریاضی  و شکل زیر قابل تعریف است:

در این فرمول X_ij نشان دهنده هر مشاهده (هر داده) در آزمایش، µ میانگین کل جمعیتی که از طریق نمونه‌ها با فرض صفر مورد بررسی قرار می‌گیرد، τ_j اثر هر تیمار و ԑ_ij اثر خطای آزمایشی است. به گفته دیگر اجزا تشکیل دهنده هر داده در این طرح، میانگین جمعیت، اثر تیمار و اثر عوامل ناشناخته می‌باشند. کمیت‌های فوق به غیر از µ می‌توانند مثبت یا منفی باشند. همچنین از فرمول بالا چنین برمی‌آید که اگر بین تیمارها اختلافی وجود نداشته باشد و خطای آزمایشی به صفر تقلیل پیدا بکند مقدار هر مشاهده برابر میانگین کل جمعیت خواهد بود یعنی تمام داده‌ها برابر µ خواهند بود.

جدول تجریه و تحلیل واریانس طرح کاملا تصادفی

جهت تجزیه واریانس طرح کاملا تصادفی شده از جدول زیر استفاده می‌شود که در آن فرمول‌های تعریفی و عملی مجموع مربعات، درجات آزادی و میانگین مربعات برای منابع تغییر در این طرح آمده است.

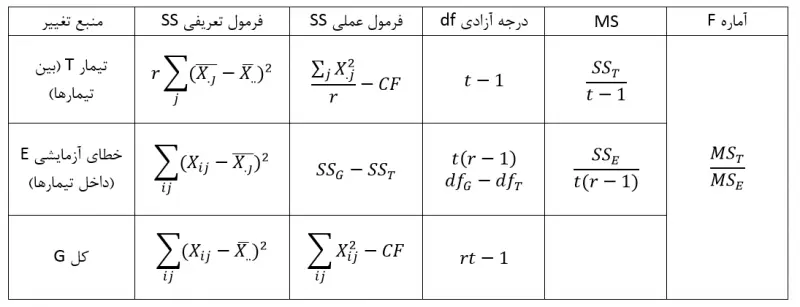
حال برای روشن‌تر شدن موضوع به حل یک مثال می‌پردازیم. جدول زیر نقشه و داده‌های حاصل از مطالعه اثر گوگرد در کاهش بیماری گال پوستی سیب زمینی را نشان می‌دهد. هدف از بکار بردن گوگرد افزایش اسیدیته خاک می‌باشد چون پاتوژن این بیماری در خاک اسیدی چندان فعال نیست. علاوه بر کرت‌های بدون گوگرد که به عنوان شاهد در نظر گرفته شده‌اند، تاثیر 3 مقدار از گوگرد در بهار و 3 مقدار از آن در پاییز با مقادیر 336، 673 و 1345 کیلوگرم در هکتار مورد مقایسه بوده است.

بدین ترتیب روی هم رفته 7 تیمار در آزمایش بکار رفته است. صفت مورد اندازه‌گیری درصد آلودگی در غده‌های سیب زمینی است. در واقع در هر واحد آزمایشی 100 غده به تصادف مورد مشاهده قرار گرفته و درصد آلودگی آن (از صفر تا 100) یادداشت و معدل‌گیری به عمل آمده است.

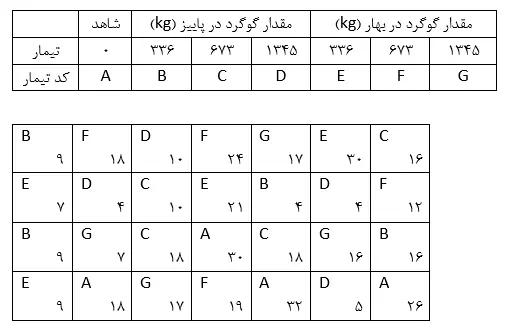
داده‌ها را بر حسب تیمارها می‌توان به شرح زیر تنظیم کرد و محاسبات جدول تجزیه واریانس را انجام داد:

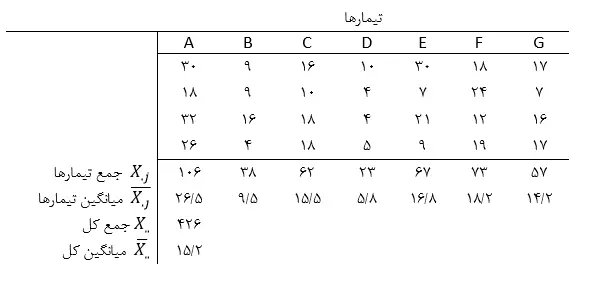
برای محاسبه تغییرات مربوط به منابع مختلف کافی است که فرمول‌های ستون سوم و چهارم جدول تجزیه واریانس بکار برده شوند و اولین گام محاسبه SSها است.

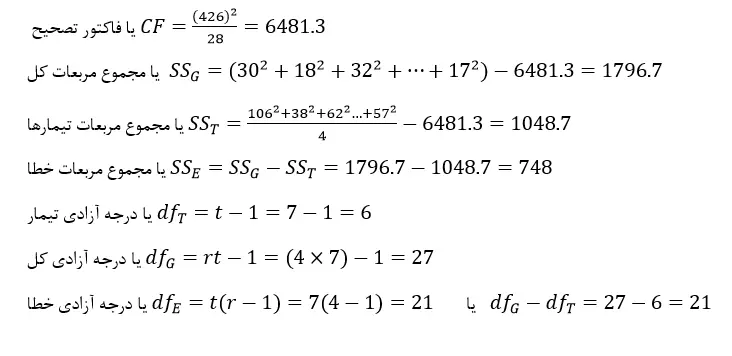
بدین ترتیب طبق عملیات فوق مجموع مربعات و درجات آزادی برای کل، تیمار و خطای آزمایشی محاسبه گردید. حال میانگین مربعات از تقسیم SSها به درجات آزادی مربوطه به‌دست می‌آید. پس:

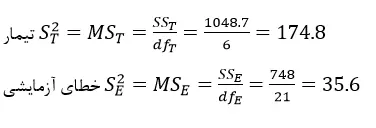
محاسبات فوق بر اساس فرضیه H₀ انجام گرفته‌اند. یعنی فرض شده است که تیمارها نمونه‌های مختلف از یک جمعیت و تکرارها تعداد افراد مشاهده شده در هر نمونه‌اند. عدم وجود اختلاف معنی‌دار بین آن‌ها نشان خواهد داد که نمونه‌های فرضی انتخاب شده می‌توانند متعلق به یک جمعیت آماری باشند. یعنی تغییرات بین تیمارها و داخل تیمارها ناشی از تصادف است.

اگر حاصل تقسیم میانگین مربعات تیمارها بر میانگین مربعات خطا کوچکتر از عدد F جدول فیشر – اسندکور باشد، چنین تصور می‌شود که منشا دو واریانس از یک جمعیت واحد بوده و بین آن‌ها اختلاف معنی‌دار نیست و اختلاف مشاهده شده تصادفی است. بر عکس اگر این نسبت بزرگتر از F جدول باشد گفته می‌شود اختلاف بین دو واریانس تصادفی نیست بلکه معنی‌دار است یعنی دو واریانس نمی‌توانند از یک جمعیت تنها به‌دست آمده باشند.

بنابراین معنی‌دار بودن F نشان می‌دهد که بین تیمارها اختلاف قابل ملاحظه و غیرتصادفی وجود دارد. طرز استفاده از جداول F بدین ترتیب است که درجه آزادی تیمار را در ردیف بالای جدول و درجه آزادی خطا را در ستون اول دست چپ پیدا کرده و عددی که از تقاطع این دو درجه آزادی به‌دست می‌آید F جدول خواهد بود و حداکثر نسبت ناشی از تغییرات تصادفی در طرح آزمایشات را نشان می‌دهد.

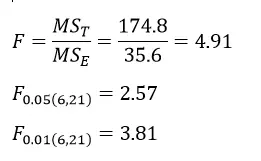
چون F محاسبه شده در این طرح برابر 91/4 و بزرگتر از 57/2 و 81/3 می‌باشد، نتیجه می‌گیریم که با اطمینان 99 درصد تیمارهای بکار برده شده از نظر تاثیر بر روی کاهش بیماری گال پوستی سیب زمینی اختلاف معنی‌داری داشته‌اند.

جدول تجزیه واریانس طرح کاملا تصادفی شده مربوط به تاثیر گوگرد در کاهش بیماری گال پوستی سیب زمینی در ادامه آمده است:

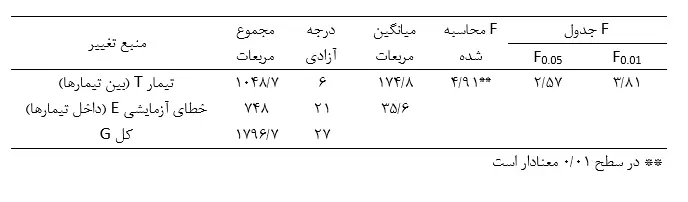
طرح آزمایشات کاملا تصادفی شده

در آزمایش‌های مزرعه‌ای مشاهده می‌شود که کرت‌های نزدیک به هم برای صفات اندازه‌گیری شده تشابه بیشتری نسبت به کرت‌های دور از هم نشان می‌دهند. همچنین در آزمایش‌های دامی، حیوانات هم وزن و هم سن واکنش نزدیکتری نسبت به یک عامل نشان می‌دهند. بدین سبب پیش از انجام آزمایش باید یک گروهبندی برای واحدهای آزمایشی انجام گیرد تا بتوان پراکندگی‌هایی که در اثر تفاوت‌های بین گروه‌ها ایجاد می‌شود محاسبه و از خطای آزمایشی جدا کرد و بدینوسیله خطای آزمایشی را تقلیل و دقت آزمایش را بالا برد.

به عنوان مثال در آزمایش مقایسه ساییدگی انواع لاستیک‌ها باید به عواملی مثل نوع خودرو و موقعیت قرارگیری لاستیک توجه کرد. در این موارد به جای استفاده از طرح کاملا تصادفی شده از طرح بلوکی کاملا تصادفی شده استفاده می‌کنند. در طرح‌های بلوکی کاملا تصادفی شده واحدهای آزمایشی طوری گروه‌بندی می‌شوند که تعداد واحدها در هر دسته مساوی تعداد تیمارها باشد.

در این صورت هر گروه را یک بلوک کامل می‌گویند (یا یک تکرار). در هر بلوک سعی می‌شود که واحدهای آزمایشی مربوطه حتی‌الامکان مشابه باشند و تمام عملیات و مشاهدات به طور یکنواخت در آن‌ها عملی گردد. در این شرایط فرض بر این است که اختلاف مشاهده شده بین واحدهای آزمایشی در هر بلوک عمدتا ناشی از خود تیمارها می‌باشد.

در این طرح آزمایشات به علت تشکیل بلوک‌های کامل، دقت آزمایش بیشتر از طرح کاملا تصادفی شده است. از سوی دیگر مانند طرح مربع لاتین که بعدا شرح داده خواهد شد از نظر تعداد تیمار و تعداد تکرار محدودیت زیادی ندارد. بنابراین در انواع تحقیقات بیشترین مورد استعمال را پیدا کرده است. هرگاه بنا به دلایلی یک بلوک یا یک تیمار از آزمایش حذف شود اشکالی در تجزیه آماری روی نخواهد داد. هرگاه یک یا چند واحد آزمایشی از بین برود می‌توان با روش ویژه‌ای آن‌ها را برآورد کرد. تنها عیب آن در این است که اگر ماده آزمایشی در دو جهت غیر یکنواخت باشد، این طرح کارایی لازم را نخواهد داشت.

در این طرح آزمایشات دو عامل قابل کنترل وجود دارد. یکی از این دو عامل تیمار و دیگری بلوک است که در طرح کاملا تصادفی شده وجود نداشت. هدف از وارد کردن عامل بلوک در یک طرح، کاهش خطای آزمایشی است. یعنی با حذف تغییرات مربوط به بلوک‌ها مقایسه‌ی تیمارها، که هدف اصلی در هر آزمایش است، به طور دقیق انجام می‌گیرد. با توجه به مطالب فوق مدل ریاضی طرح به صورت زیر تعریف می‌شود:

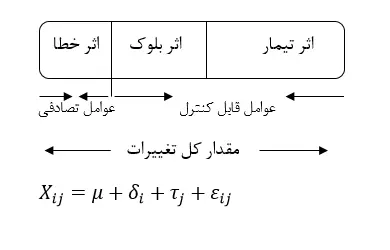
یعنی مقدار عددی هر مشاهده (X_ij) از مجموع اثرات بلوک (δ_i)، تیمار (τ_j)، خطای آزمایشی (ԑ_ij) و میانگین کل جمعیت (µ) حاصل می‌شود. لذا در طرح‌های بلوکی کاملا تصادفی شده، مقدار کل تغییرات را می‌توان به تغییرات مربوط به تیمارها، بلوک‌ها و خطای آزمایشی تقسیم کرد.

در این طرح باید یک واریانس اضافی مربوط به بلوک‌ها نیز محاسبه شود. جهت تجزیه واریانس از جدول زیر استفاده می‌شود که در آن فرمول‌های تعریفی و عملی مجموع مربعات، درجات آزادی و میانگین مربعات برای منابع مختلف تغییر در این طرح آمده است.

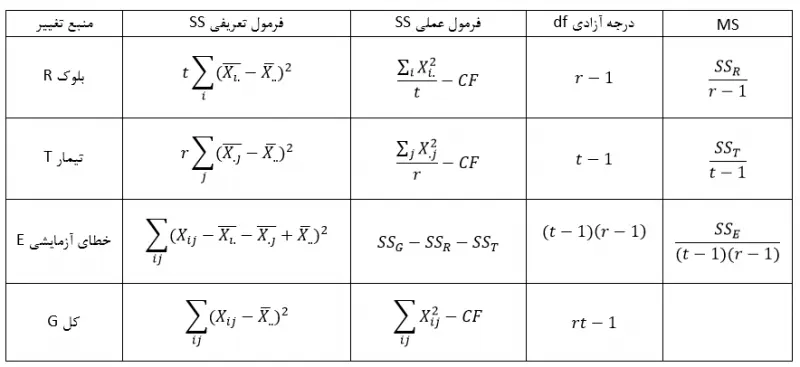
در یک آزمایش 5 رقم یونجه در یک طرح آزمایشات بلوکی کاملا تصادفی شده از نظر مقدار علوفه تولیدی مورد مقایسه قرار گرفته‌اند و تعداد بلوک یا تکرار 4 بوده است. هر واحد آزمایشی حدود 15 متر مربع بود. نتایج حاصل از یکی از برداشت‌ها در جدول زیر آمده است:

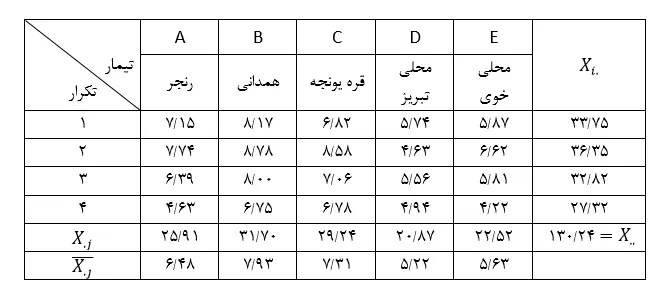
در ادامه محاسبات مربوط به مجموع مربعات، درجات آزادی و میانگین مربعات برای منابع مختلف تغییر در این طرح آمده است:

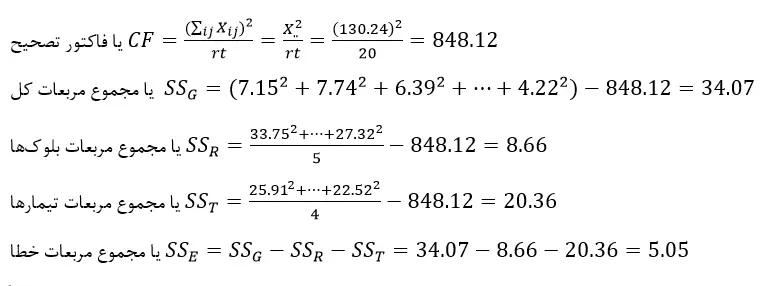
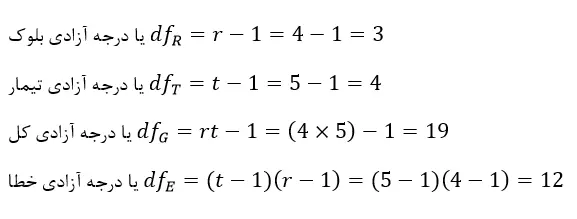
چون F_T محاسبه شده در این طرح آزمایشات برابر 12/12 و بزرگتر از 26/3 و 41/5 می‌باشد، نتیجه می‌گیریم که با اطمینان 99 درصد تیمارهای بکار برده شده از نظر مقدار علوفه توليدي اختلاف معنی‌داری داشته‌اند. همچنين F_R محاسبه شده در این طرح برابر 88/6 و بزرگتر از 49/3 و 95/5 می‌باشد، نتیجه می‌گیریم که با اطمینان 99 درصد بلوک‌هاي بکار برده شده از نظر مقدار علوفه توليدي اختلاف معنی‌داری داشته‌اند.

هنگامي که بين بلوک‌ها اختلاف معني‌دار پيدا مي‌شود بدين معني است که يا بلوک‌بندي صحيح انجام شده است و يا عمليات اجرايي در بلوک‌هاي مختلف يکسان نبوده است. در نهايت جدول تجزیه واریانس طرح بلوکي کاملا تصادفی شده مربوط به مقدار علوفه توليدي در ادامه آمده است:

طرح آزمایشات مربع لاتين

اين طرح هنگامي به کار مي‌رود که روند غيريکنواختي در ماده آزمايشي در دو جهت باشد. براي مثال در زميني که حاصلخيزي آن در دو جهت غربي – شرقي و جنوبي – شمالي تغيير مي‌کند مي‌توان با به کار بردن اين طرح آزمایشات اختلاف در حاصلخيزي را در دو جهت محاسبه و از خطاي آزمايشي کم کرد. بدين منظور تيمارها در داخل بلوک‌ها به دو صورت مختلف يعني به صورت رديف‌ها و ستون‌ها گروه‌بندي مي‌شوند. در آزمايشات دامي گروه‌بندي دوطرفه بر اساس عواملي مانند سن، وزن، جنس دام و … صورت مي‌گيرد.

طرح به اين دليل مربع لاتين نام گرفته‌است که در آن تعداد تکرار معادل تيمارهاي آزمايشي است. به عنوان مثال براي مربع لاتيني که در آن 4 تيمار و 4 تکرار به کار رفته باشد، 4 ستون عمودي تشکيل داده مي‌شود که معمولا با اعداد لاتين I، II، III و IV نشان داده مي‌شوند و 4 رديف افقي وجود خواهد داشت که با اعداد 1، 2، 3 و 4 مشخص مي‌شوند.

در اين طرح چون هر تيمار در هر رديف و هر ستون وجود دارد لذا تغييرات مربوط به بلوک رديفي و بلوک ستوني از تغييرات بين تيمارها جدا مي‌شود و بنابراين تيمار را مي‌توان به‌طور دقيق‌تر مقايسه کرد. از اين رو در اين طرح خطاي آزمايشي کوچکتر و دقت آزمايش بيشتر مي‌شود.

عيب عمده طرح مربع لاتين در اين است که در آن تعداد تکرار مساوي تعداد تيمار بوده و محدوديتي از نظر تعداد تيمار به وجود مي‌آيد. چون در صورت زياد بودن تيمار عمليات تکنيکي مشکل‌تر مي‌شود، لذا اگر تعداد تيمار بيشتر از 8 باشد معمولا از اين طرح استفاده نمي‌شود. از سوي ديگر درجه آزادي خطاي آزمايشي در اين طرح در مقايسه با طرح‌هاي قبلي مشابه کوچکتر است.

در طرح آزمایشات مربع لاتين کرت‌ها طوري تنظيم مي‌شوند که دو منبع قابل کنترل به وجود مي‌آيد. به يکي از اين منابع بلوک‌هاي ستوني و به ديگري بلوک‌هاي رديفي اطلاق مي‌شود. بدين ترتيب اجزا تغييرات کل به صورت زير نمايش داده مي‌شود:

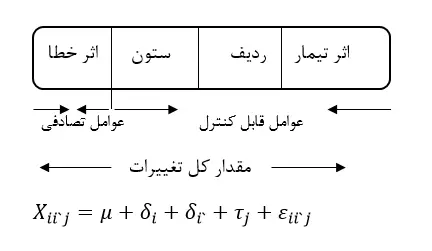
که در آن X_{ii`j</sub> هر مشاهده، µ ميانگين کل جمعيت، δ<sub>i</sub> اثر رديف، δ<sub>i`} اثر ستون، τ_j اثر تيمار و ԑ_ii`j اثر خطاي آزمايشي مي‌باشد.

جهت تجزیه واریانس از جدول زیر استفاده می‌شود که در آن فرمول‌های تعریفی و عملی مجموع مربعات، درجات آزادی و میانگین مربعات برای منابع مختلف تغییر در این طرح آمده است:

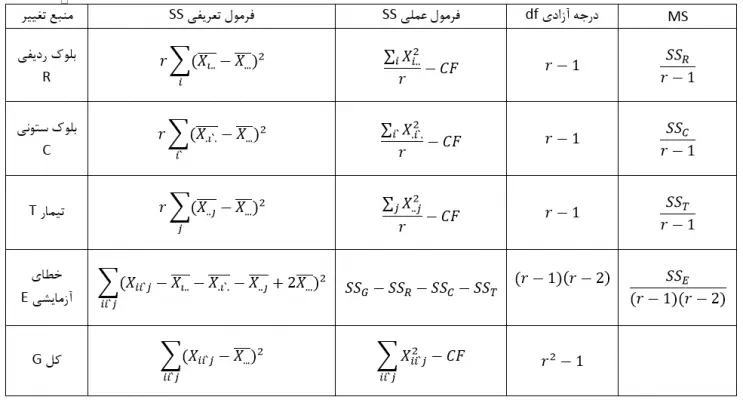
یکی از اولین آزمایش‌های مربوط به طرح مربع لاتین توسط فیشر انجام گرفته است. در این آزمایش اثر 5 کود مختلف به همراه شاهد روی واریته‌ای از سیب‌زمینی مورد ارزیابی قرار گرفته است. این 5 کود و شاهد (6 تیمار) با حروف زیر کدگذاری شده‌اند:

A = شاهد (بدون کود)

B = فسفات با دوز معمولی

C = فسفات با دوز دو برابر

D = ازت

E = فسفات + ازت

F =  فسفات با دوز دو برابر + ازت

 جدول زیر عملکرد حاصل از هر واحد آزمایشی را بر حسب کیلوگرم و نقشه طرح نشان می‌دهد. در این جدول جمع مربوط به ردیف‌ها و ستون‌ها نیز دیده می‌شود.

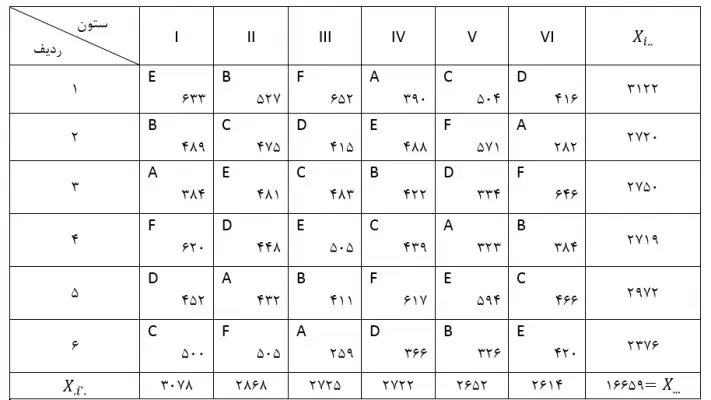
حال برای به‌دست آوردن جمع مربوط به تیمارها باید جدول دیگری بر حسب تیمارها تنظیم کرد:

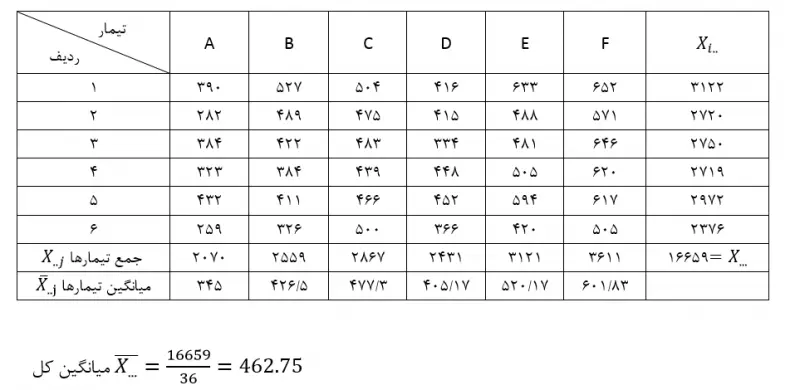
در ادامه محاسبات مربوط به مجموع مربعات، درجات آزادی و میانگین مربعات برای منابع مختلف تغییر و جدول تجزیه واریانس در این طرح آمده است:

حال می‌توان SSها را در جدول تجزیه واریانس وارد و مقادیر MS و F را مستقیما در جدول محاسبه کرد.

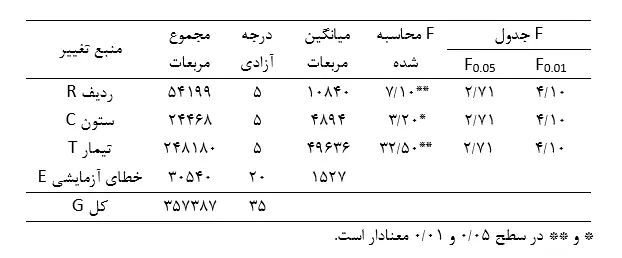
مطابق جدول تجزیه واریانس بین ستون‌ها در سطح معنی‌داری 05/0 و بین ردیف‌ها و تیمارها در سطح معنی‌داری 01/0 اختلاف معنی‌داری وجود دارد.

طرح آزمایشات یکی از تخصصی ترین مطالب آماری است،حال که با نحوه محاسبات مربوط به تجزیه واریانس 3 طرح پایه کاملا تصادفی شده، بلوکی کاملا تصادفی شده و مربع لاتین آشنا شدیم، انجام محاسبات با نرم‌افزارهایی مثل SPSS یا SAS آسان‌تر خواهد بود. خاطر نشان می‌کنم برای حصول نتایج قابل استناد، در ابتدا باید نقشه طرح به درستی تعریف شود. تیم آمار پیشرو آماده ارائه مشاوره رایگان در زمینه انتخاب طرح  متناسب با نوع آزمایش و فرضیات مورد بررسی، انجام نمونه‌برداری، تهیه نقشه طرح، ورود داده به نرم‌افزار و انجام محاسبات مربوطه با نرم‌افزارهایی مثل R، SPSS، SAS و… خواهد بود.برای ارتباط و دریافت مشاوره می توانید به بخش مشاوره آماری رایگان مراجعه کنید.

چنانچه علاقمند به مباحث آماری هستید و می خواهید با نرم افزار های حوزه طرح آزمایشات آشنا شوید می توانید از جدید ترین مطالبی که بر روی سایت منتشر خواهد شد با دنبال کردن صفحه اینستاگرام آمار پیشرو با خبر شوید.

قطعا اجرا طرح آزمایشات نیاز به متخصصان خبره و با تجربه دارد. شما نیز اگر پروژه ای دارید که می خواهید با کیفیت مناسب، در مدت زمان کوتاه و با قیمت مناسب اجرا شود، می توانید در قسمت ثبت سفارش اجرای این پروژه ها را به متخصصان علم آمار در شرکت آمار پیشرو بسپارید.