همبستگی جزئی و همبستگی نیمه جزئی اجرای آن در SPSS
- 18 شهریور 1399
- 1:49 ب.ظ
- بدون نظر
فهرست مطالب
همبستگی جزئی و نیمه جزئی یکی از انواع همبستگی ها است. در این مطلب ابتدا همبستگی را تعریف کرده و سپس با مثالی ملموس همبستگی جزئی و نیمه جزئی اجرا خواهیم کرد.
هرگاه رگرسیون خطی دارای چند متغیر مستقل باشد محاسبه همبستگی هر یک از متغیرهای مستقل با متغیر وابسته مستلزم فرمان همبستگی جزئی و نیمه جزئی است. با اجرای این فرمان همبستگی هر یک از متغیرهای مستقل با متغیر وابسته تحت عنوان همبستگی مرتبه صفر (Zero-Order Correlation) در جدول ضرایب رگرسیون ارائه میشود. همبستگی مرتبه صفر یک متغیر مستقل همبستگی آن متغیر با متغیر وابسته بدون به حساب آوردن اثر متغیرهای مستقل دیگر است.شما می توانید برای دریافت هر چه بهتر مفهوم رگرسیون از طریق این لینک به مطلب رگرسیون چیست برسید.
قبل از ارائه توضیحات در رابطه با همبستگی جزئی و نیمه جزئی لازم است بار دیگر مفهوم همبستگی را یادآوری کنیم.
همبستگی جزئی و نیمه جزئی چیست ؟
قبل از ارائه توضیحات در رابطه با همبستگی جزئی و نیمه جزئی لازم است بار دیگر مفهوم همبستگی را یادآوری کنیم.
همبستگی:
همبستگی ضریب رگرسیون استاندارد دو متغیره است و همانطور که میدانید ضریب زاویه یا شیب خط رگرسیون متغیر وابسته Y با متغیر مستقل X است که مقادیر آنها به صورت مقادیر استاندارد است. اگر مقدار استاندارد Y را با ZY و مقدار استاندارد X را با ZX نشان دهیم همبستگی با نماد r عبارت است از نسبت کوواریانس مقادیر استاندارد X و Y به واریانس مقادیر استاندارد X:
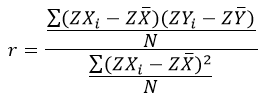
که در آن ZXi مقدار استاندارد Xi است و ZYi مقدار استاندارد Yi و میانگین مقادیر استاندارد متغیر مستقل X و میانگین مقادیر استاندارد متغیر وابسته Y.
از آنجا که میانگین مقادیر استاندارد صفر است و واریانس مقادیر استاندارد یک میشود:
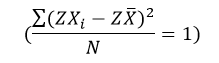
در این صورت:
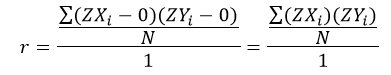
و سرانجام:
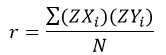
به این ترتیب همبستگی نسبت مجموع حاصل ضرب مقادیر استاندارد Y و X به تعداد کل عنصرهاست.
در دادههای مبتنی بر نمونه احتمالی در فرمول فوق n-1 جایگزین N استفاده میشود:
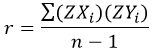
به عنوان مثال همبستگی حقوق ماهیانه (متغیر وابسته) با تحصیلات (متغیر مستقل) کارکنان شرکت بهار مقادیر X و Y با توجه به مجموع حاصلضرب مقادیر استاندارد دو متغیر مذکور عبارت است از:
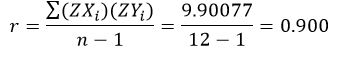

مقدار همبستگی فوق مبین آن است که به ازای یک واحد انحراف استاندارد افزایش در میزان تحصیلات (متغیر مستقل) 900/0 انحراف استاندارد به حقوق ماهیانه (متغیر وابسته) افزوده میشود. علامت جبری r نیز مبین جهت رابطه است. مقدار مثبت r مبین رابطه مستقیم (صعودی) است و مقدار منفی بیانگر رابطه معکوس (نزولی).
نکته: همبستگی را میتوان با جذر گرفتن از ضریب تعیین r2 دو متغیره به دست آورد و یا ضریب تعیین را با مجذور کردن همبستگی پیدا کرد. با این همه هر یک از این دو ضریب معنای معینی دارند: r2 ضریبی است برای نشان دادن شدت رابطه دو متغیر کمی و نسبتی از تغییر متغیر وابسته است که متغیر مستقل تبیین میکند در حالی که r شیب خط رگرسیون اندازه استاندارد Y با اندازه استاندارد X است.
فرمان همبستگی در SPSS
همبستگی r در برنامه کامپیوتری SPSS با همان فرمان رگرسیون خطی برای دو متغیر (متغیر وابسته و متغیر مستقل) محاسبه شده و مقدار آن در جدول ضرایب رگرسیون Coefficients در ستون ضرایب استاندارد شده Standardized Coefficients یا به اختصار ضریب بتا beta ارائه میشود. جدول 2 جدول ضرایب رگرسیون گزارش اجرای فرمان رگرسیون خطی Linear Regression دو متغیر کمی تحصیلات (X) و حقوق ماهانه (Y) شرکت بهار است. همانطور که میبینیم مقدار همبستگی r تحصیلات (X) و حقوق ماهانه (Y) در ستون ضریب استانداردشده 900/0 گزارش شده است. مقدار همبستگی r در این جدول همان است که با فرمول به دست آوردیم.
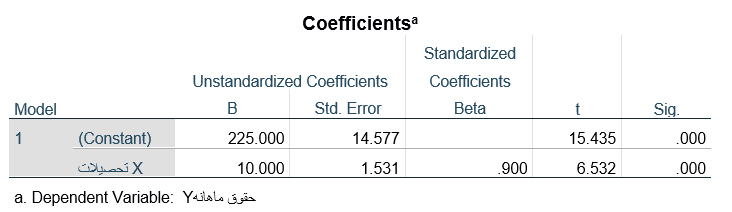
جدول 3 هم جدول ضرایب Coefficients گزارش اجرای فرمان رگرسیون خطی Linear Regression دو متغیر کمی تحصیلات (X) و حقوق ماهانه (Y) شرکت آتیه است. مقدار همبستگی r تحصیلات (X) و حقوق ماهانه (Y) در ستون ضریب استاندارد شده 953/0 گزارش شده است و بدان معناست که به ازای یک واحد انحراف استاندارد افزایش در میزان تحصیلات (متغیر مستقل) کارکنان شرکت آتیه 953/0 انحراف استاندارد به حقوق ماهانه (متغیر وابسته) آنها افزوده میشود.
فرمان همبستگی جزئی و نیمه جزئی در SPSS
برای فرمان همبستگی جزئی و نیمه جزئی Part and Partial Correlation از همان فرمان رگرسیون خطی استفاده میکنیم: در بخش تحلیل Analyze در قسمت رگرسیون Regression قسمت خطی Linear… را کلیک میکنیم.
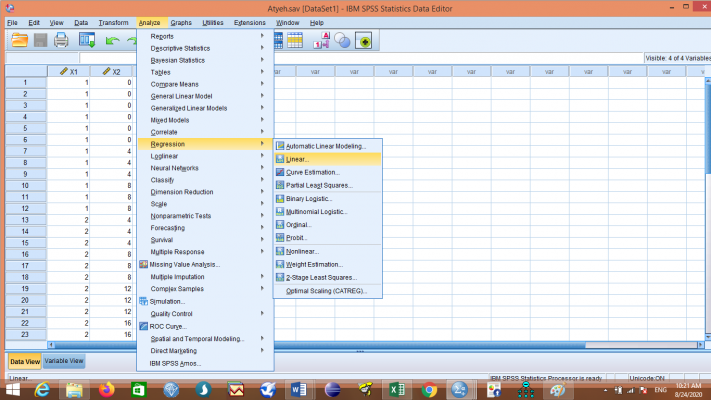
با باز شدن صفحه رگرسیون خطی Linear Regression متغیر وابسته را از بین متغیرهای خانه سمت چپ انتخاب میکنیم و به خانه متغیر وابسته Dependent انتقال میدهیم. همینطور متغیر یا متغیرهای مستقل مورد نظر خود را به خانه متغیر مستقل Independent(s) منتقل میکنیم.
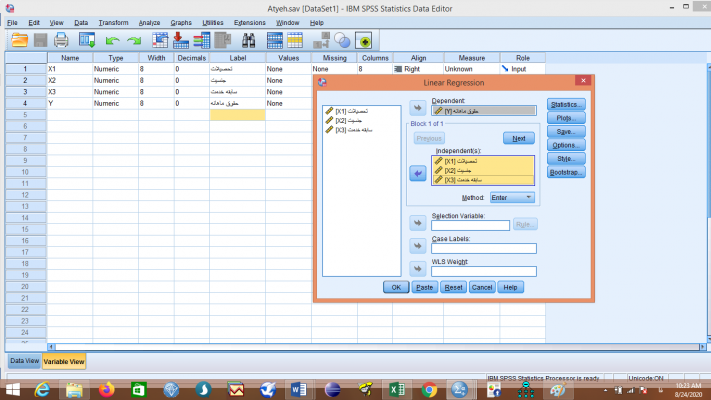
سپس قسمت آمارهها Statistics… را کلیک میکنیم.
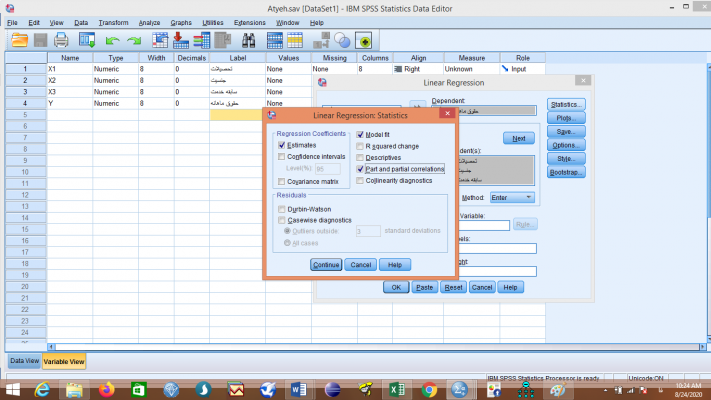
در صفحه آمارههای رگرسیون خطی Linear Regression: Statistics قسمت همبستگی جزئی و نیمه جزئی Part and Partial Correlation را فعال ساخته و ادامه Continue را کلیک کرده و به دنبال آن در صفحه رگرسیون خطی فرمان را تایید OK میکنیم.
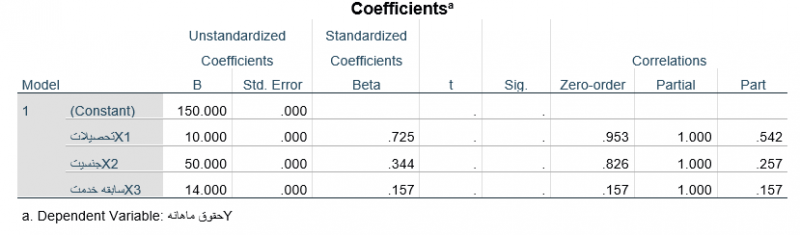
جدول زیر گزارش اجرای فرمان همبستگی جزئی و نیمه جزئی Part and Partial Correlation در فرمان رگرسیون خطی متغیر حقوق ماهانه (Y) با جنسیت (X2) و تحصیلات (X1) و سابقه خدمت (X3) کارکنان شرکت آتیه است. همبستگی مرتبه صفر تک تک متغیرهای مستقل با متغیر وابسته در قسمت همبستگی Correlation ستون اول (Zero-Order) آمده است.
به عنوان مثال همبستگی مرتبه صفر متغیر مستقل تحصیلات (X1) با متغیر وابسته حقوق ماهانه (Y) معادل 953/0 است و بدان معناست که همبستگی متغیر تحصیلات با متغیر حقوق ماهانه 953/0 است. مقدار این همبستگی مرتبه صفر معادل همان مقداری است که با رگرسیون دو متغیره به دست آمده و در جدول ارائه شده است.
فرمان همبستگی دو متغیره
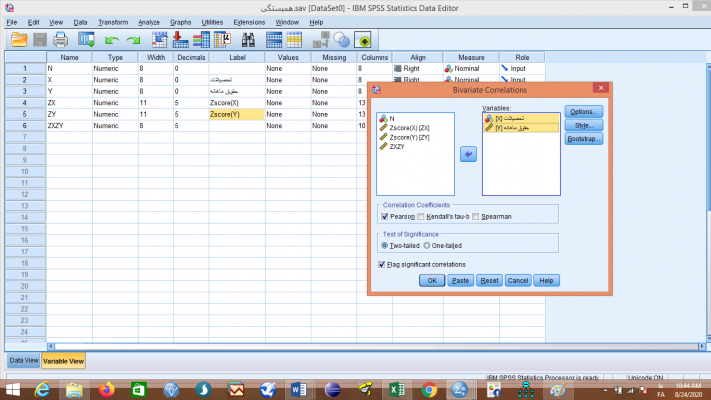
همبستگی r را میتوان به طور مستقل با فرمان همبستگی دو متغیره هم به دست آورد. فرمان همبستگی دو متغیره در بخش تحلیل Analyze قسمت همبستگی Correlate قسمت دو متغیره Bivariate قرار دارد. با ورود به این قسمت و کلیک کردن آن صفحه همبستگی دو متغیره Bivariate Correlation باز میشود.
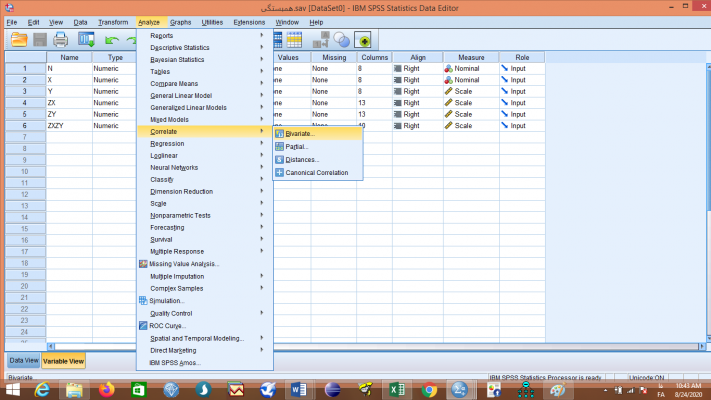
سپس در صفحه همبستگی دو متغیره Bivariate Correlation متغیرهای مورد نظر خود را از بین متغیرهای خانه سمت چپ انتخاب میکنیم و به خانه متغیرها Variables انتقال میدهیم و در همین صفحه فرمان همبستگی دو متغیره را تایید OK میکنیم.
جدول زیر جدول گزارش همبستگی Correlation اجرای فرمان همبستگی دو متغیره تحصیلات (X) و حقوق ماهانه (Y) شرکت بهار است. همانطور که می بینیم مقدار همبستگی r تحصیلات (X) و حقوق ماهانه (Y) در خانه محل تلاقی دو متغیر 900/0 گزارش شده است. مقدار همبستگی r در این جدول همان است که با فرمول یا فرمان رگرسیون خطی Linear Regression دو متغیره به دست آوردیم.
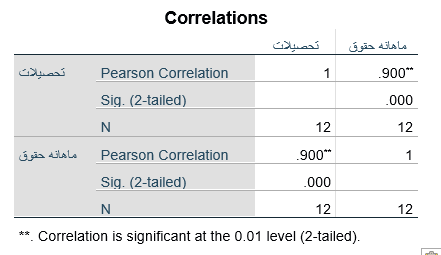
در جدول همبستگی Correlation به هر متغیر یک ردیف و سه سطر اختصاص دارد. سطر اول حاوی مقدار همبستگی آن متغیر با سایر متغیرها (از جمله خود متغیر) است. سطر دوم مبین مقدار معناداری و سطر سوم مبین تعداد عنصرهایی است که در آن دو متغیر دارای پاسخ معتبرند. به عنوان مثال در جدول زیر ستون آخر سطر اول نشان میدهد مقدار همبستگی متغیر حقوق ماهانه با متغیر تحصیلات 900/0 و سطر دوم نشان میدهد مقدار معناداری این همبستگی 000/0 است و سطر سوم نشان میدهد این همبستگی بر اساس 12 عنصر دارای پاسخ معتبر محاسبه شده است.
همبستگی جزئی
همبستگی جزئی (یا همبستگی تفکیکی) متغیر وابسته (Y) با متغیر مستقل (X) همبستگی آن دو متغیر با کنترل اثر متغیرهای مستقل دیگر بر هر دو است. به عبارت دیگر همبستگی جزئی دو متغیر Y و X همبستگی آن دو متغیر بعد از برداشتن اثر متغیرهای مستقل دیگر از روی هر دو متغیر Y و X است.
برای محاسبه همبستگی جزئی دو متغیر Y و X هر کدام از دو متغیر را به عنوان متغیر وابسته با متغیرهای مستقل دیگر رگرسیون خطی میگیریم و باقی ماندههای هر یک از آنها را به صورت یک متغیر در نظر گرفته و بین آن دو متغیر باقیمانده با فرمول همبستگی میگیریم.
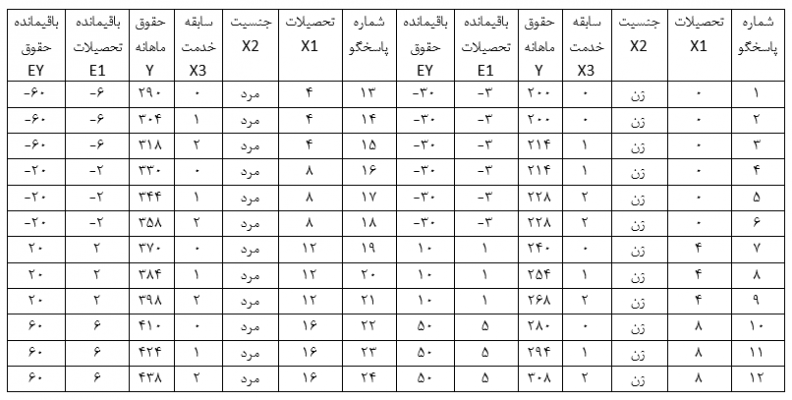
به عنوان مثال برای محاسبه همبستگی جزئی دو متغیر حقوق ماهانه (Y) و تحصیلات (X1) کارکنان شرکت آتیه ابتدا بین تحصیلات (X1) به عنوان متغیر وابسته با متغیرهای مستقل دیگر که جنسیت (X2) و سابقه خدمت (X3) هستند رگرسیون میگیریم و باقی ماندههای آن را تحت عنوان متغیر باقیمانده تحصیلات (E1) ضبط میکنیم. همچنین بین حقوق ماهانه (Y) به عنوان متغیر وابسته با متغیرهای مستقل دیگر (جنسیت X2 و سابقه خدمت X3) رگرسیون میگیریم و باقیماندههای آن را تحت عنوان متغیر باقی مانده حقوق (EY) ضبط میکنیم.
حال با فرمول و یا فرمان همبستگی دو متغیره بین آن دو متغیر باقی مانده همبستگی دو متغیره میگیریم که همبستگی جزیی دو متغیر حقوق ماهانه (Y) و تحصیلات (X1) کارکنان شرکت آتیه است.
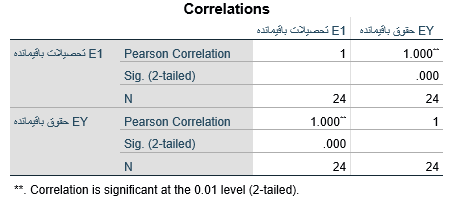
در این مثال همبستگی جزئی دو متغیر مذکور 00/1 میشود و بدان معناست که با برداشتن اثر جنسیت (X2) و سابقه خدمت (X3) از روی متغیر حقوق ماهانه (Y) و تحصیلات (X1) همبستگی این دو متغیر 00/1 است. به عبارت دیگر بعد از برداشتن اثر جنسیت (X2) و سابقه خدمت (X3) از روی متغیر تحصیلات و متغیر حقوق ماهانه به ازای یک واحد انحراف استاندارد افزایش در باقیمانده متغیر تحصیلات 00/1 واحد انحراف استاندارد به باقیمانده متغیر حقوق ماهانه افزوده میشود.
کاربرد همبستگی جزئی
همبستگی جزئی دو متغیر اساساً برای کنترل رابطه دو متغیر با ثابت نگه داشتن آماری اثر سایر متغیرهایی است که شاید هر دو متغیر به آنها وابسته باشند. کاربرد دیگر همبستگی جزئی تعیین سودمندی افزودن یک متغیر مستقل به رگرسیون خطی است. هرگاه همبستگی جزئی متغیر وابسته (Y) با متغیر مستقل (X) از صفر بیشتر باشد مبین سودمندی افزودن آن متغیر مستقل به رگرسیون خطی و افزایش قدرت تبیین کنندگی مدل رگرسیون است و هر چه مقدار همبستگی جزئی بیشتر باشد سودمندی افزودن آن متغیر مستقل به رگرسیون خطی بیشتر است.
تعریف: همبستگی جزیی دو متغیر Y و X همبستگی آن دو متغیر بعد از برداشتن اثر متغیرهای مستقل دیگر از روی هر دو متغیر Y و X است.
همبستگی جزئی هر متغیر مستقل با متغیر وابسته در برنامه کامپیوتری SPSS با فرمان همبستگی جزئی و نیمه جزئی Part and Partial Correlation فرمان رگرسیون خطی محاسبه میشود. مقدار همبستگی جزئی هر متغیر مستقل با متغیر وابسته در جدول ضرایب رگرسیون خطی Coefficients در قسمت همبستگی Correlation ستون دوم (Partial) ارائه میشود. به عنوان مثال در جدول 4 همبستگی جزیی متغیر مستقل تحصیلات (X1) با متغیر وابسته حقوق ماهانه (Y) کارکنان شرکت آتیه معادل 000/1 درج شده است که معادل همان مقداری است که در جدول 7 به دست آمد.
همبستگی جزیی متغیر وابسته با متغیر مستقل را می توان به طور مستقیم با فرمان همبستگی جزئی هم به دست آورد.
فرمان همبستگی جزئی
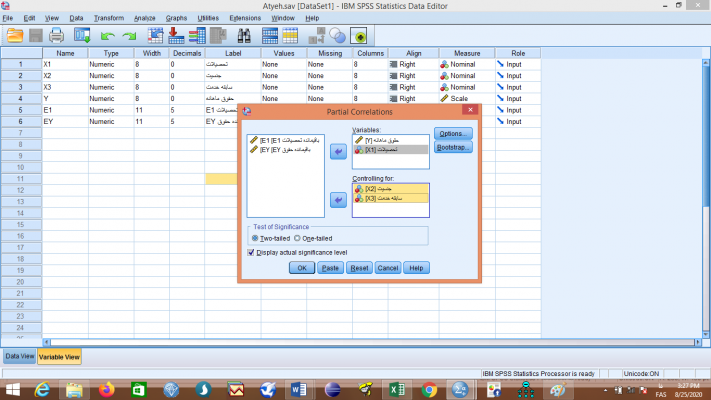
فرمان همبستگی جزئی Partial Correlation در بخش تحلیل Analyze در قسمت همبستگی Correlate قسمت جزئی Partial قرار دارد. با ورود به این قسمت (کلیک کردن آن) صفحه همبستگی جزئی Partial Correlation باز میشود. سپس در صفحه فرمان همبستگی جزیی Partial Correlation متغیر وابسته و متغیر مستقل را از بین متغیرهای خانه سمت چپ انتخاب میکنیم و به خانه متغیرها Variables: و متغیر یا متغیرهای کنترل را به خانه کنترل Controlling for: انتقال میدهیم. سپس در همین صفحه فرمان همبستگی جزئی Partial Correlation را تایید OK میکنیم.
جدول 8 گزارش اجرای فرمان همبستگی جزیی دو متغیر حقوق ماهانه (Y) و تحصیلات (X1) کارکنان شرکت آتیه با کنترل جنسیت (X2) و سابقه خدمت (X3) است. همبستگی جزئی دو متغیر مذکور 00/1 است و بدان معناست که با برداشتن اثر جنسیت (X2) و سابقه خدمت (X3) از روی متغیر حقوق ماهانه (Y) و تحصیلات (X1) همبستگی این دو متغیر 00/1 است.
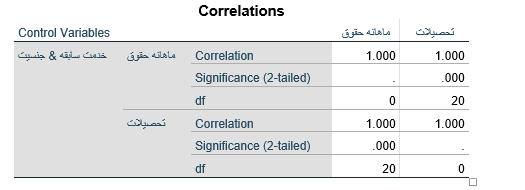
دامنه مقادیر همبستگی جزئی دو متغیر بین صفر به معنای فقدان رابطه باقیماندههای دو متغیر تا 1 به معنای رابطه کامل باقیماندههای دو متغیر است. هرگاه ضریب تعیین مدل رگرسیون ۱ شود یعنی تمام تغییر متغیر وابسته را متغیرهای مستقل مدل رگرسیون تبیین کنند همبستگی جزیی هر متغیر مستقل ۱ میشود زیرا بعد از برداشتن اثر متغیرهای دیگر از روی متغیر مستقل و وابسته همه باقیمانده متغیر وابسته را باقیمانده متغیر مستقل تبیین میکند و متغیر وابسته دیگر باقی ماندهای نخواهد داشت.
نکته: در جایی که همبستگی جزیی یک متغیر مستقل ۱ شود مبین آن است که ضریب تعیین مدل رگرسیون ۱ است.
همبستگی نیمه جزئی
همبستگی نیمه جزئی یا همبستگی نیمه تفکیکی متغیر وابسته (Y) با متغیر مستقل (X) همبستگی آن دو متغیر با کنترل اثر متغیرهای مستقل دیگر بر متغیر مستقل است. به عبارت دیگر همبستگی نیمه جزئی متغیر وابسته با یک متغیر مستقل همبستگی آن دو متغیر بعد از برداشتن اثر متغیرهای مستقل دیگر از روی آن متغیر مستقل است.
برای محاسبه همبستگی نیمه جزئی دو متغیر Y و X از متغیر X به عنوان متغیر وابسته با متغیرهای مستقل دیگر رگرسیون خطی میگیریم و باقیماندههای آن را یک متغیر محسوب میکنیم و با فرمول بین آن دو متغیر باقیمانده و متغیر وابسته Y همبستگی دو متغیره میگیریم.
به عنوان مثال برای محاسبه همبستگی نیمه جزئی دو متغیر حقوق ماهانه (Y) و تحصیلات (X1) کارکنان شرکت آتیه ابتدا بین تحصیلات (X1) به عنوان متغیر وابسته با متغیرهای مستقل دیگر که جنسیت (X2) و سابقه خدمت (X3) هستند رگرسیون میگیریم و باقیماندههای آن را تحت عنوان متغیر باقیمانده تحصیلات (E1) ثبت میکنیم. حال با فرمول یا فرمان همبستگی دو متغیره بین باقیمانده تحصیلات (E1) و حقوق ماهانه (Y) همبستگی دو متغیره میگیریم که همبستگی نیمه جزیی دو متغیر حقوق ماهانه (Y) و تحصیلات (X1) کارکنان شرکت آتیه است.
همبستگی نیمه جزیی دو متغیر مذکور 542/0 است و بدان معناست که با برداشتن اثر جنسیت (X2) و سابقه خدمت (X3) از روی متغیر تحصیلات (X1) همبستگی متغیر تحصیلات با متغیر حقوق ماهانه (Y) معادل 542/0 است. به عبارت دیگر بعد از برداشتن اثر جنسیت و سابقه خدمت از روی متغیر تحصیلات به ازای یک واحد انحراف استاندارد افزایش در باقیمانده متغیر تحصیلات 542/0 واحد انحراف استاندارد به حقوق ماهانه افزوده میشود.
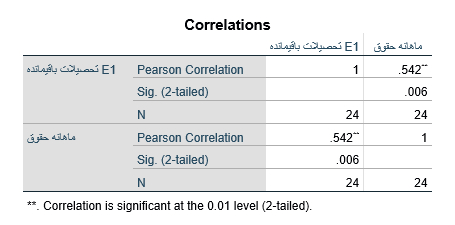
همبستگی نیمه جزئی هر متغیر مستقل با متغیر وابسته در برنامه کامپیوتری SPSS با فرمان همبستگی جزئی و نیمه جزئی Part and Partial Correlation فرمان رگرسیون خطی که پیشتر به میان آمد محاسبه میشود. مقدار همبستگی نیمه جزیی هر متغیر مستقل با متغیر وابسته در جدول ضرایب رگرسیون خطی Coefficients در قسمت همبستگی Correlation ستون سوم (Part) ارائه میشود.
به عنوان مثال در جدول 4 همبستگی نیمه جزیی متغیر مستقل تحصیلات (X1) با متغیر وابسته حقوق ماهانه (Y) کارکنان شرکت آتیه معادل 542/0 درج شده است که معادل همان مقداری است که در جدول 9 به دست آمد.
کاربرد همبستگی نیمه جزیی
همبستگی نیمه جزئی دو متغیر برای نشان دادن همبستگی خالص متغیر مستقل (X) با متغیر وابسته (Y) و به تبع آن اثر خالص متغیر مستقل بر متغیر وابسته است. به عبارت دیگر همبستگی نیمه جزئی برای محاسبه اثر متغیر مستقل (X) بر متغیر وابسته (Y) بعد از کنار گذاشتن اثر سایر متغیرهای مستقل موثر بر متغیر مستقل به کار میرود. محاسبه اثر خالص متغیر مستقل به روابط بین متغیرهای مستقل مدل رگرسیون بستگی دارد.
تعریف: همبستگی نیمه جزیی دو متغیر وابسته Y و متغیر مستقل X همبستگی آن دو متغیر بعد از برداشتن اثر متغیرهای مستقل دیگر از روی X است.
در این مطلب سعی کردیم به صورت کامل همبستگی و به خصوص همبستگی جزئی و نیمه جزئی را برای شما شرح دهیم. اما در اجرای این مطلب امکان دارد به مشکلاتی برخورد کنید برای پاسخ به این مشکلات گاهی اوقات نیاز دارید تا افراد با تجربه تر شما را راهنمایی کنند. ما برای شما این امکان را با کمک گرفتن از متخصصان آمار پیشرو فراهم کردیم.شما می توانید از این پل ارتباطی به صورت رایگان استفاده کنید. این پل ارتباطی در بخش مشاوره آماری رایگان موجود است.
همبستگی جزئی و همبستگی نیمه جزئی دو نوع از همبستگی است شما می توانید مطالب بیشتر را در این حوزه در وبلاگ سایت آمار پیشرو ملاحظه کنید. همچنین اگر علاقه مند هستید می توانید جدید ترین مطالب علم آمار که در سایت بارگذاری می شود با دنبال کردن صفحه اینستاگرام آمار پیشرو با خبر شوید.
در بسایری از موارد همبستگی جزئی و نیمه جزئی در پروژه های مختلف پیچیدگی های متفاوتی را دارد. در این زمان بهتر است شما از نظر متخصصان استفاده کنید. به همین منظور امکانی فراهم شده تا این پروژه ها را به افراد خبره بسپارید. این افراد صفر تا صد پروژه شما را می توانند انجام دهند. به همین منظور شما می توانیددر قسمت ثبت سفارش در سایت آمار پیشرو و با تکمیل کردن فرم پروژه خود را به افراد مجرب بسپارید.
هبستگی چیست؟
همبستگی میزان و نوع ارتباط بین دو متغیر را نشان میدهد.
تعریف ریاضی همبستگی چیست؟
همبستگی نسبت مجموع حاصل ضرب مقادیر استاندارد Y و X به تعداد کل عنصرهاست.
همبستگی جزئی چیست؟
همبستگی جزئی دو متغیر Y و X همبستگی آن دو متغیر بعد از برداشتن اثر متغیرهای مستقل دیگر از روی هر دو متغیر Y و X است.
همبستگی نیمه جزئی چیست؟
همبستگی نیمه جزئی یا همبستگی نیمه تفکیکی متغیر وابسته (Y) با متغیر مستقل (X) همبستگی آن دو متغیر با کنترل اثر متغیرهای مستقل دیگر بر متغیر مستقل است.