تحلیل آماری با SPSS
- نویسنده : لادن عباس نیا
- ارسال شده در: نوامبر 18, 2024
- ارسال دیدگاه: ۰
نرمافزار SPSS یک نرمافزار معروف برای انجام تحلیلهای آماری است. این نرمافزار در سال ۱۹۶۸ توسط شرکت SPSS برای انجام تحلیلهای آماری دادههای علوم اجتماعی ساخته شد و در سال ۲۰۰۹ به مالکیت شرکت IBM درآمد. در حال حاضر از این نرمافزار در شاخههای متنوعی از علوم مانند بازاریابی، سلامت، جامعهشناسی، رفتاری، روانشناسی، مدیریت، دادهکاوی و بسیاری دیگر استفاده میشود. این نرمافزار دارای ویژگیهای ممتاز و جالب توجهی است که باعث رواج روزافزون آن در انجام انواع تحلیلهای آماری شده است. برخی از ویژگیهای برجسته نرمافزار SPSS عبارتند از:
- محیط کاربرپسند و آسان برای استفاده کاربرانی از سطوح مبتدی، متوسط و پیشرفته،
- دسترسی به مجموعه گستردهای از ابزارهای آماری،
- اجرای ساده تحلیلهای آماری،
- ارائه پاسخهای سریع و قابل اعتماد،
- ارائه جداول و نمودارهای آماری مفید و کاربردی،
- یکپارچگی با نرمافزارهای رایگان (مانند R و پایتون).
از جمله مواردی که نرمافزار SPSS بسیار مورد استفاده میگیرد، انجام تحلیلهای آماری پایاننامههای دانشجویی است. دانشجویان مقاطع تکمیلی که برای بررسی فرضیات یا پاسخ به سوالات پایاننامه خود باید دادههای گرداوریشده را تحلیل کنند، اغلب نرمافزار SPSS را انتخاب میکنند. دلایل محبوبیت این نرمافزار در بین دانشجویان نیز همانند دلایلی است که پیشتر مطرح شد. البته معتبر بودن نتایج SPSS نیز دلیلی است که باید بر آن تأکید کرد. به طوری که معمولاً در فصل سه پایاننامههای دانشجویی، باید نام و نسخه نرمافزار(های) مورداستفاده در تحلیل دادهها ذکر شود و چنان چه از SPSS برای این منظور استفاده شده باشد، با ذکر نام آن بر اعتبار نتایج حاصل از پایاننامه افزوده میشود. البته آشنایی با روشهای مختلف آماری و تسلط بر نحوه اجرای آنها در SPSS نیز یکی دیگر از الزامات حاصل شدن نتایج معتبر است. دانشجویان و پژوهشگران برای به دست آوردن تسلط کافی بر روشهای آماری و کسب مهارت در زمینه این نرمافزار میتوانند از مطالب آموزشی شرکت آمارپیشرو بهره بگیرند.
در ادامه برای آشنایی بیشتر با نحوه استفاده از SPSS، به تعدادی از روشهای آماری متداول که با این نرمافزار قابل انجام هستند اشاره میشود. در هر قسمت، یک توضیح کوتاه از هدف آزمون آماری، کاربرد آن، خروجی آزمون در SPSS و راهنمایی درباره تفسیر آن ارائه شده است.
مجموعه دادههای دبیرستان
برای مثالهایی که در این مطلب مطرح شدهاند، از مجموعه دادههای دبیرستان استفاده شده است. این دادهها شامل اطلاعاتی مربوط به ۲۰۰ دانشآموزان دبیرستانی است. متغیرهای حاضر در این مجموعه داده عبارتند از: جنسیت (female) شامل دختر یا پسر؛ نژاد (race) شامل اسپانیایی، آسیایی، آفریقایی-آمریکایی و سفید؛ وضعیت اقتصادی-اجتماعی (ses) شامل پایین، متوسط و بالا؛ نوع مدرسه (schtyp) شامل عمومی و خصوصی؛ نوع برنامه درسی (prog) شامل عمومی، دانشگاهی و فنی و حرفهای؛ و نمرات دروس نوشتاری (write)، خوانش (read)، ریاضی (math)، علوم (science) و علوم اجتماعی (socst) که مقادیری بین صفر تا صد میتوانند داشته باشند. چند ردیف اول این مجموعه داده در شکل زیر به نمایش درآمده است:
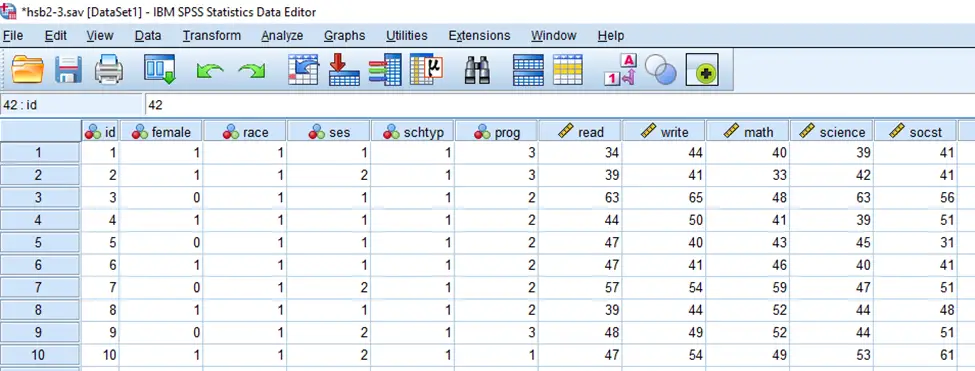
آزمون تی تکنمونهای
توسط آزمون تی تکنمونهای میتوانیم آزمون کنیم آیا میانگین نمونه (مربوط به یک متغیر فاصلهای که دارای توزیع نرمال است) به طور معنیدار با یک مقدار فرضیهای متفاوت است. به عنوان مثال، در مجموعه دادههای دبیرستان، فرض کنید میخواهیم آزمون کنیم آیا متوسط نمره نوشتاری (write) با ۵۰ به طور معنیدار متفاوت است. با اجرای آزمون تی تکنمونهای در SPSS نتایج زیر به دست میآید:
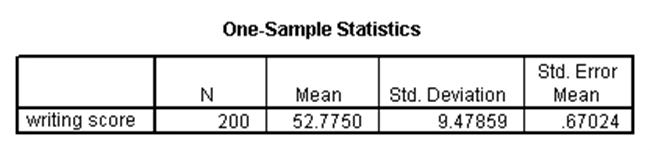

با توجه به جداول بالا که در خروجی آزمون تکنمونهای SPSS ظاهر شده میبینیم که میانگین متغیر write برای نمونه حاضر در مجموعه دادههای دبیرستان برابر با ۵۲.۷۷۵ است (جدول اول). در جدول دوم با توجه به آن که p-مقدار این آزمون کمتر از ۰.۰۵ است، میتوان نتیجه گرفت که میانگین نمرات نوشتاری دانشآموزان با مقدار ۵۰ به طور معنیدار متفاوت است. لذا میانگین نمره نوشتاری دانشآموزان به طور معنیدار بزرگتر از ۵۰ است.
نکته) وقتی در خروجیهای SPSS، p-مقدار برابر با ۰.۰۰۰ نشان داده میشود بدین معنی است که عدد آن تا سه رقم اعشار صفر است. این یعنی p-مقدار از ۰.۰۵ نیز کوچکتر است.
آزمون میانه تکنمونهای (آزمون ویلکاکسون)
این آزمون به ما امکان میدهد بررسی کنیم آیا میانه نمونهای مورد نظر ما دارای تفاوت معنیدار با یک مقدار فرضیهای است. این آزمون برای متغیرهایی مناسب است که نرمال نیستند و از نوع پیوسته یا ترتیبی هستند. برای مثال این آزمون نیز باز هم از متغیر نمره نوشتاری استفاده و بررسی میکنیم آیا میانه نمونهای دارای تفاوت معنیدار با ۵۰ است. نتایج آزمون ویلکاکسون برای این مثال در SPSS بدین صورت است:
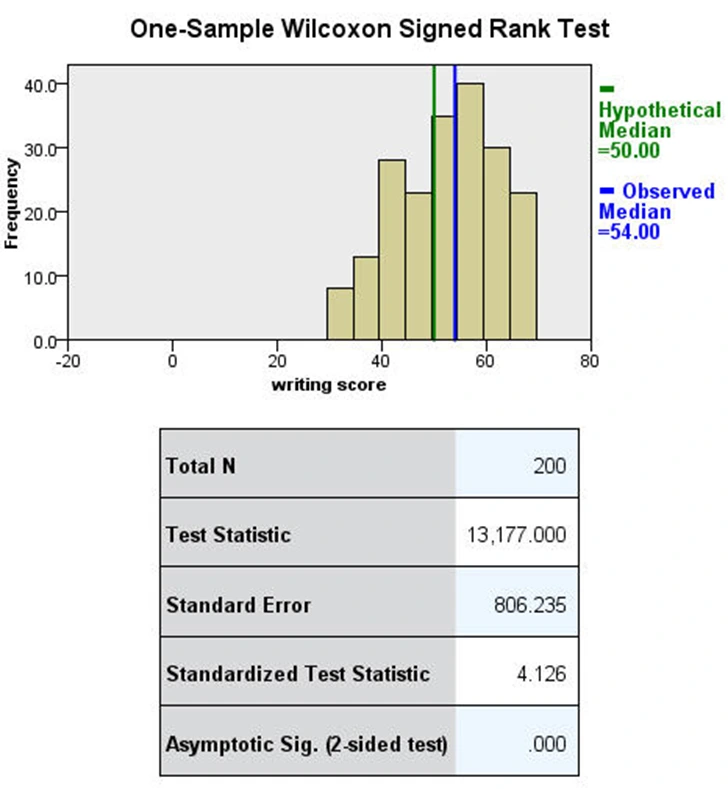
خروجی SPSS برای آزمون ویلکاکسون در قالب یک نمودار و یک جدول ارائه شده است. با توجه به نمودار بالا ملاحظه میشود که میانه نمونه نمره نوشتاری برابر با ۵۴.۰۰ است. با توجه به جدول نیز چون p-مقدار این آزمون کمتر از ۰.۰۵ است، میتوان نتیجه گرفت این میانه به طور معنیدار با مقدار ۵۰ متفاوت است.
آزمون دوجملهای (binomial)
آزمون دوجملهای به ما امکان میدهد بدانیم آیا نسبت موفقیتها در یک متغیر وابسته دوگروهی دارای تفاوت معنیدار با یک مقدار فرضیهای است. به عنوان مثال، در مجموعه دادههای دبیرستان، بررسی میکنیم آیا نسبت دختران (مربوط به متغیر female) به طور معنیدار با ۰.۵ متفاوت است. نتایج آزمون دوجملهای برای این مثال با استفاده از SPSS بدین صورت است:
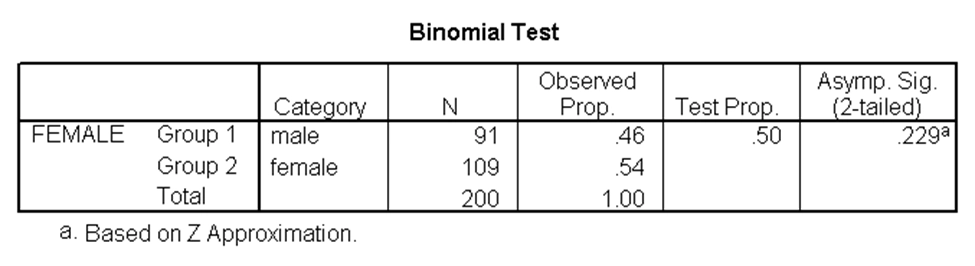
در جدول بالا p-مقدار برابر با ۰.۲۲۹ شده و از ۰.۰۵ بزرگتر است، بنابراین آزمون دوجملهای معنیدار نیست. به عبارت دیگر، نسبت زنان دارای تفاوت معنیدار با ۰.۵ نیست.
آزمون نیکویی برازش کیدو (Chi-square goodness of fit)
با استفاده از این آزمون میتوان بررسی کرد آیا نسبتهای مشاهدهشده برای یک متغیر کیفی، دارای تفاوت معنیدار با نسبتهای فرضیهای است. مثلاً در یک جامعه شامل افراد از نژادهای مختلف، باور داریم نسبتهای هر کدام از نژادها بدین صورت است: اسپانیایی ۱۰ درصد، آسیایی ۱۰ درصد، آفریقایی آمریکایی ۱۰ درصد و سفیدپوست ۷۰ درصد. حال میخواهیم بدانیم آیا نسبتهای مشاهدهشده دارای تفاوت معنیدار با نسبتهای فرضیهای مذکور هستند. نتیجه آزمون نیکویی برازش کیدو در SPSS برای این مثال عبارت است از:
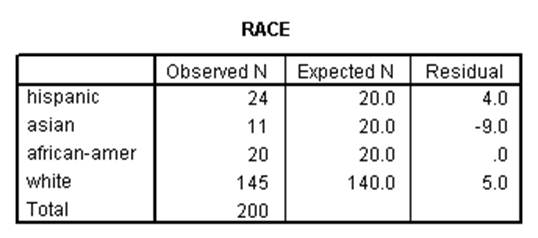

در جدول اول نسبتهای مشاهدهشده برای هر کدام از نژادها به همراه نسبتهای موردانتظار (فرضیهای) آمده است. در جدول دوم، مقدار آماره کیدوی نیکویی برازش برابر با ۵.۰۲۹ با ۳ درجه آزادی است. برای این آماره، p-مقدار برابر با ۰.۱۷۰ و بزرگتر از ۰.۰۵ است، لذا نسبتهای مشاهدهشده دارای تفاوت معنیدار با نسبتهای فرضیهای که در نظر گرفتیم نیست.
آزمون تی دونمونهای مستقل (Two independent samples t-test)
از این آزمون در حالتی استفاده میشود که میخواهیم بدانیم آیا یک متغیر وابسته کمّی که دارای توزیع نرمال است، دارای میانگینهای متفاوت در دو گروه مستقل است. به عنوان مثال در مجموعه دادههای دبیرستان، اگر بخواهیم میانگین نمره نوشتاری (write) را در دو گروه دختران و پسران مقایسه کنیم، نتایج آزمون تی دونمونهای مستقل در SPSS عبارت است از:
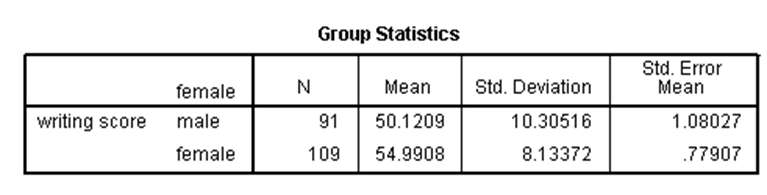
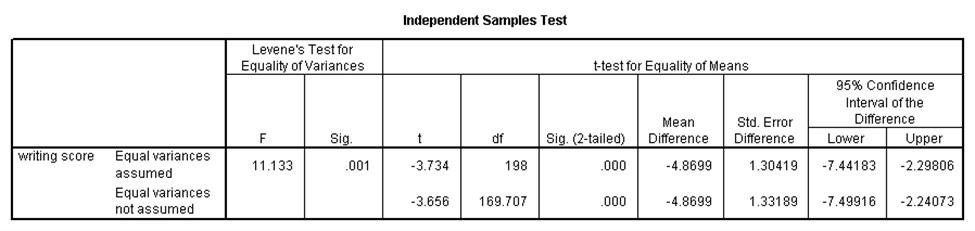
در جدول اول میبینیم که میانگین نمره نوشتاری برای پسران و دختران در نمونه، به ترتیب برابر با ۵۰.۱۲ و ۵۴.۹۹ است. حال برای آن که بدانیم آیا این دو میانگین به طور معنیدار متفاوت هستند، باید ابتدا بدانیم واریانس نمره نوشتاری در دو گروه برابر است یا خیر. برای این کار باید از آزمون لِوِن استفاده کنیم. در جدول دوم، مقدار آماره لِوِن برابر با ۱۱.۱۳ و p-مقدار آن ۰.۰۰۱ شده که کوچکتر از ۰.۰۵ است، لذا واریانس دو گروه برابر نیست. حال باید به نتایج آزمون تی دونمونهای مستقل که برای حالت نابرابری واریانس ارائه شده نگاه کنیم. در حالت نابرابری واریانس، مقدار آماره تی برابر با ۳.۶۵۶- شده و p-مقدار آن کوچکتر از ۰.۰۵ است، لذا میانگین نمره نوشتاری برای دختران و پسران دارای تفاوت معنیدار است. با توجه به مقادیر میانگین نمونهای نیز، چون مقدار میانگین نمره پسران بزرگتر از دختران است، میتوان گفت میانگین نمره نوشتاری پسران به طور معنیدار بزرگتر از میانگین نمره نوشتاری دختران است.
آزمون من ویتنی (Mann-Whitney)
آزمون من ویتنی، نسخه ناپارامتری آزمون تی دونمونهای مستقل است و میتواند برای زمانی به کار رود که توزیع متغیر وابسته نرمال نیست (متغیر وابسته میتواند کمّی یا رتبهای باشد). حال در مجموعه دادههای دبیرستان، آزمون من ویتنی را برای نمره نوشتاری در دو گروه دختران و پسران اجرا میکنیم. نتایج آن بدین صورت است:
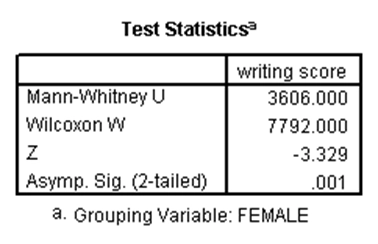
همان طور که در جدول بالا میبینیم، p-مقدار برابر با ۰.۰۰۱ شده که کوچکتر از ۰.۰۵ است، لذا در نمره نوشتاری بین دختران و پسران تفاوت معنیدار وجود دارد.
آزمون کیدو
این آزمون زمانی استفاده میشود که میخواهیم بدانیم آیا رابطهای بین دو متغیر کیفی وجود دارد. به عنوان مثال، در مجموعه دادههای دبیرستان فرض کنید میخواهیم وجود رابطه معنیدار بین نوع مدرسه (schtyp) و جنسیت دانشآموزان (female) را بررسی کنیم. برای این کار در SPSS از جدول توافقی استفاده میشود و مشروط بر آن است که فراوانی هر کدام از خانههای این جدول ۵ یا بیشتر باشد (چنان چه این شرط برقرار نباشد، باید از آزمون دقیق فیشر استفاده کرد که فقط برای متغیرهایی استفاده میشود که دارای دو گروه باشند). در مثال حاضر این شرط برقرار است و نتایج آزمون کیدو در SPSS در ادامه میآید.
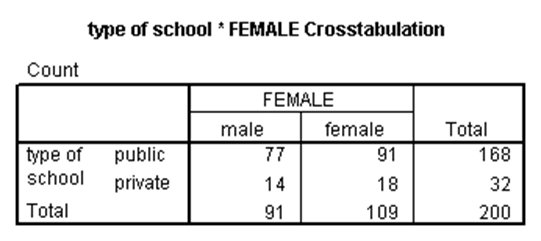
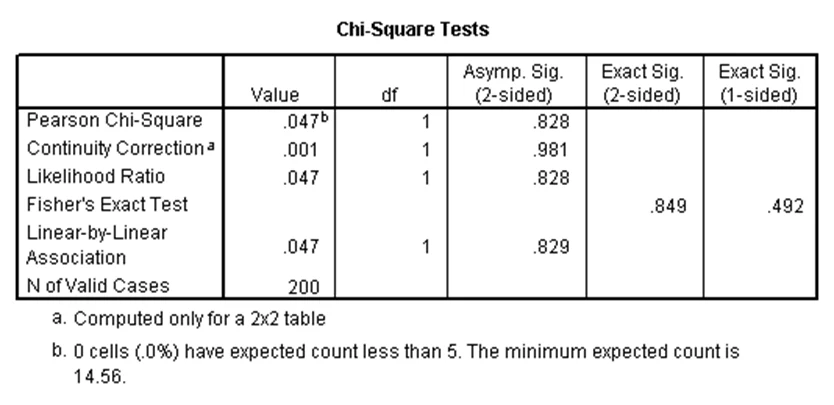
اولین جدول بالا، جدول توافقی نوع مدرسه و جنسیت را نشان میدهد. همان طور که ملاحظه میشود، برای هر کدام از چهار خانه این جدول، مقدار فراوانی بزرگتر از ۵ است. در جدول دوم مقدار آماره کیدو با یک درجه آزادی برابر با ۰.۰۴۷ شده است. برای این آماره، p-مقدار برابر با ۰.۸۲۸ شده که بزرگتر از ۰.۰۵ است. لذا رابطه معنیدار بین نوع مدرسه و جنسیت وجود ندارد.
تحلیل واریانس یکطرفه (One-way ANOVA)
آنوای یکطرفه برای حالتی استفاده میشود که یک متغیر مستقل کیفی (با دو یا بیشتر گروه) و یک متغیر وابسته کمّی نرمال داریم و میخواهیم تفاوتهای موجود بین میانگینهای متغیر وابسته در هر کدام از گروههای متغیر مستقل را بررسی کنیم. مثلاً در مجموعه دادههای دبیرستان، میخواهیم بدانیم آیا میانگینهای نمره نوشتاری (write) بین سه گروه برنامه درسی (prog) متفاوت است. نتایج تحلیل واریانس یکطرفه برای این مثال در SPSS در ادامه ارائه شده است.
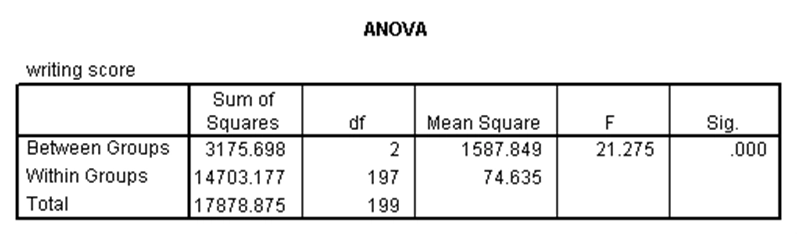
همان طور که در جدول تحلیل واریانس بالا مشاهده میشود، p-مقدار آماره فیشر کوچکتر از ۰.۰۵ است. لذا میانگین متغیر وابسته در گروههای متغیر مستقل دارای تفاوت معنیدار است.
آزمون کروسکال والیس (Kruskal Wallis)
این آزمون برای زمانی است که یک متغیر وابسته کمّی غیرنرمال و یک متغیر مستقل کیفی (با دو گروه یا بیشتر) داریم. در حقیقت، آزمون کروسکال والیس نسخه ناپارامتری آزمون تحلیل واریانس یکطرفه و نسخه تعمیمیافته آزمون من ویتنی است. برای نشان دادن این آزمون در SPSS از مثال مشابه برای آزمون تحلیل واریانس یکطرفه استفاده میکنیم، ولی فرض میکنیم نمره نوشتاری دارای توزیع نرمال نیست. نتایج بدین صورت است:
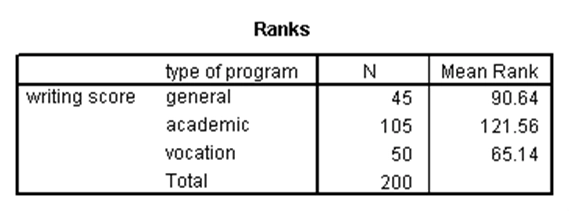

در جدول اول، میانگین رتبهها در هر کدام از گروههای برنامه درسی آمده است. در جدول دوم نیز، با توجه به آن که p-مقدار کوچکتر از ۰.۰۵ است و لذا نمره درسی بر حسب نوع برنامه درسی دارای تفاوت معنیدار است.
آزمون تی جفتی (Paired t-test)
در برخی مطالعات، به ازای هر آزمودنی دو متغیر وابسته داریم، یعنی به ازای هر آزمودنی دو مشاهده وابسته داریم. در این صورت اگر این دو متغیر دارای توزیع نرمال باشند و بخواهیم برابری میانگینهای آنها را آزمون کنیم، از آزمون تی جفتی استفاده میکنیم. در مجموعه دادههای دبیرستان، فرض کنید میخواهیم برابری میانگین نمره نوشتاری دانشآموزان (write) را با میانگین نمره خوانش آنها (read) آزمون کنیم. در این صورت، نتایج آزمون تی جفتی برای این مثال همانند جداول زیر خواهد بود:
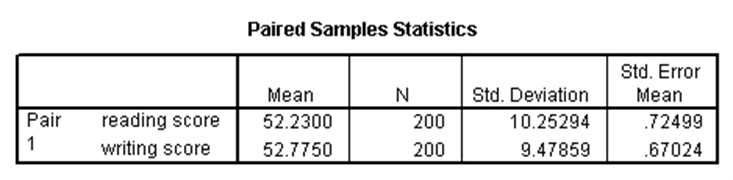
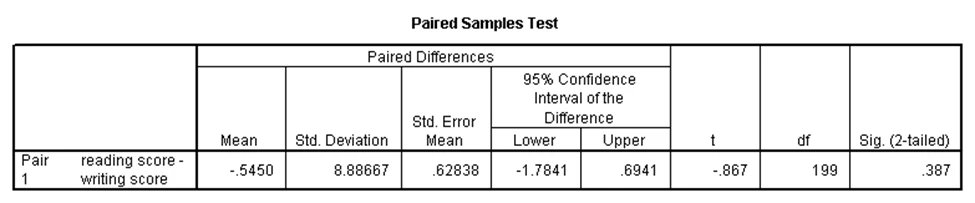
در جدول اول میبینیم که مقادیر میانگین دو متغیر نمره نوشتاری و خوانش بسیار نزدیک به هم است. با توجه به جدول دوم که در آن p-مقدار برابر با ۰.۳۸۷ و بزرگتر از ۰.۰۵ است، نتیجه میشود که تفاوت معنیدار بین میانگینهای نمرات نوشتاری و خوانش وجود ندارد.
آزمون رتبه علامتدار ویلکاکسون (Wilcoxon signed rank sum)
آزمون رتبه علامتدار ویلکاکسون، نسخه ناپارامتری آزمون تی جفتی است. بنابراین برای زمانی است که قصد داریم تفاوت بین میانههای دو متغیر وابسته را بررسی کنیم و نمیتوانیم فرض کنیم توزیع این دو متغیر نرمال است. البته هر دو متغیر باید از نوع کمّی یا ترتیبی باشند. حال آزمون رتبه علامتدار ویلکاکسون را در SPSS برای مثال تی جفتی که در بالا ذکر شد اجرا میکنیم. نتیجه آن بدین صورت است:
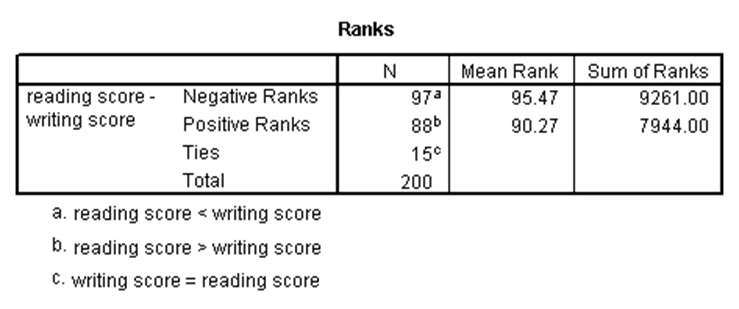
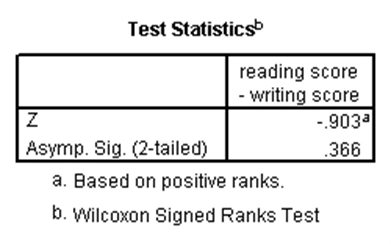
با توجه به p-مقدار در جدول دوم که برابر با ۰.۳۶۶ و بزرگتر از ۰.۰۵ است، آزمون رتبه علامتدار ویلکاکسون نیز تفاوت معنیدار بین میانههای نمرات نوشتاری و خوانش دانشآموزان را رد میکند.
آزمون مکنمار (McNemar)
آزمون مکنمار برای وقتی به کار میرود که یک متغیر وابسته دوحالتی وجود دارد که مقادیر آن در دو گروه وابسته قرار گرفتهاند و میخواهیم بدانیم آیا مقادیر متغیر وابسته بین دو گروه وابسته متفاوت است یا خیر. به عنوان مثال ابتدا در مجموعه دادههای دبیرستان، دو متغیر دودویی به نامهای himath و hiread ایجاد میکنیم که به ترتیب نشاندهنده بالا بودن نمره ریاضی و نمره خوانش دانشآموز هستند. بدین صورت که اگر نمره ریاضی دانشآموز بزرگتر از ۶۰ باشد، مقدار himath برابر با یک و در غیر این صورت برابر با صفر خواهد بود. متغیر hiread نیز به طور مشابه و با استفاده از نمره خوانش محاسبه میشود. حال با استفاده از این دو متغیر میتوان یک جدول توافقی دو در دو ایجاد کرد. فرضیه صفر نیز بدین صورت در نظر گرفته میشود که نسبت دانشآموزانی که دارای نمره بالای ریاضی هستند با نسبت دانشآموزانی که دارای نمره بالای خوانش هستند برابر است. با استفاده از آزمون مکنمار، فرضیه مذکور بررسی میشود که نتایج آن در SPSS بدین صورت است:
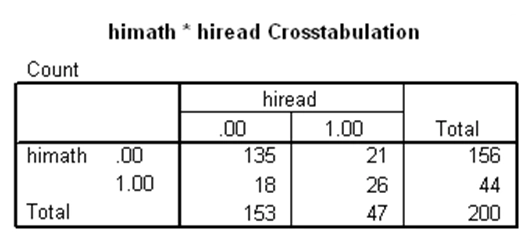
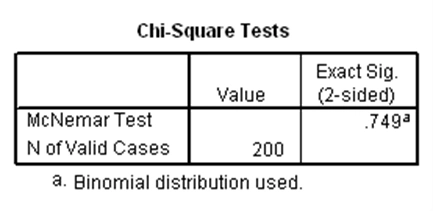
اولین جدول بالا مربوط به جدول توافقی دو متغیر himath و hiread است که فراوانیهای گروههای مختلف حاصل از آنها را میتوان دید. در جدول دوم، p-مقدار آزمون مکنمار برابر با ۰.۷۴۹ به دست آمده که چون بزرگتر از ۰.۰۵ است، فرضیه صفر رد نمیشود. لذا نمیتوان گفت بین نسبت دانشآموزانی که دارای نمره بالای ریاضی هستند با نسبت دانشآموزانی که دارای نمره بالای خوانش هستند تفاوت معنیدار وجود دارد.
آزمون فریدمن (Friedman)
آزمون فریدمن یک آزمون ناپارامتری است که وجود تفاوت معنیدار بین سه یا تعدادی بیشتر از گروههای وابسته به هم را مورد بررسی قرار میدهد. در واقع در این آزمون، یک متغیر مستقل داریم که دارای دو یا بیشتر گروه است که این گروهها به هم وابسته هستند و یک متغیر وابسته داریم که نرمال نیست (کمّی یا رتبهای است). از این آزمون برای رتبهبندی متغیرها (گروههای وابسته به هم یک متغیر مستقل) نیز میتوان استفاده کرد. به عنوان مثال در مجموعه دادههای دبیرستان، فرض کنید. میخواهیم بدانیم آیا بین نمرات سه درس خوانش، نوشتاری و ریاضی تفاوت وجود دارد. فرضیه صفر در این آزمون به صورت یکسان بودن توزیع رتبههای درسها است. نتایج SPSS برای این آزمون به صورت زیر است:
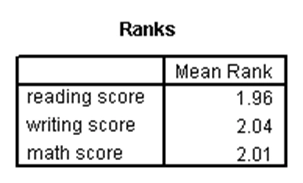
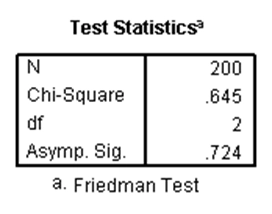
جدول اول، میانگین رتبههای هر یک از گروههای وابسته به هم متغیر مستقل را نشان میدهد. اما در جدول دوم، p-مقدار آزمون فریدمن برابر با ۰.۷۲۴ شده که چون از ۰.۰۵ بزرگتر است، نتیجه میدهد نمرات سه درس خوانش، گفتاری و ریاضی با هم دارای تفاوت معنیدار نیستند.
همبستگی پیرسون (Pearson)
آزمون همبستگی برای بررسی وجود رابطه بین دو متغیر که دارای توزیع توأم نرمال هستند استفاده میشود. در مجموعه دادههای دبیرستان، نتایج آزمون همبستگی پیرسون برای متغیرهای خوانش و نوشتاری بدین صورت است:
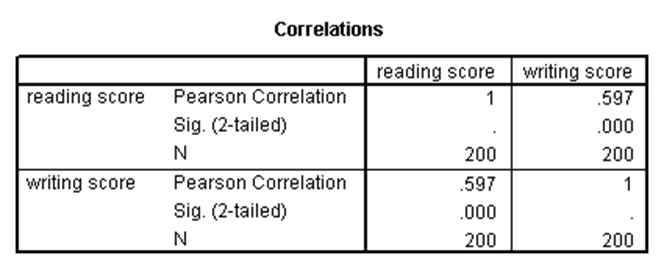
در جدول بالا، مقدار ضریب همبستگی پیرسون بین نمرات خوانش و نوشتاری برابر با ۰.۵۹۷ شده است. مقدار مثبت برای این ضریب نشاندهنده رابطهای مستقیم بین این دو متغیر است. علاوه بر این، p-مقدار این آزمون مقداری کوچکتر از ۰.۰۵ شده که نشان میدهد مقدار این ضریب همبستگی به طور معنیدار با صفر متفاوت است و لذا رابطه مشاهدهشده معنیدار است.
همبستگی اسپیرمن (Spearman)
آزمون همبستگی اسپیرمن مشابه با آزمون همبستگی پیرسون است، با این تفاوت که در آن یک یا هر دو متغیر مورد نظر، دارای توزیع نرمال نیستند (حداقل باید از مقیاس رتبهای باشند). در حقیقت، آزمون اسپیرمن نسخه ناپارامتری آزمون پیرسون است. به عنوان مثال فرض کنید نمرات خوانش و نوشتاری دانشآموزان در مجموعه دادههای دبیرستان نرمال نیستند. نتایج آزمون اسپیرمن برای بررسی وجود رابطه بین این دو متغیر در SPSS بدین صورت خواهد بود:
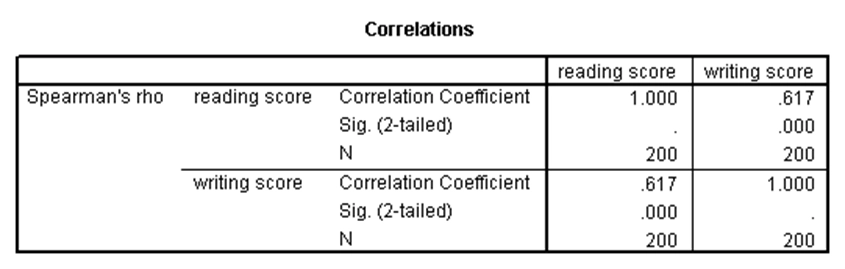
تفسیر آزمون همبستگی اسپیرمن مشابه با آزمون همبستگی پیرسون انجام میشود. با توجه به جدول بالا، ضریب همبستگی اسپیرمن بین دو متغیر برابر با ۰.۶۱۷ شده و چون p-مقدار این آزمون کوچکتر از ۰.۰۵ است، این ضریب همبستگی دارای تفاوت معنیدار با صفر است.
رگرسیون خطی ساده
استفاده از رگرسیون خطی ساده به ما این امکان را میدهد که وجود رابطه خطی بین یک متغیر مستقل (کمّی یا دوحالتی) و یک متغیر وابسته نرمال را بررسی کنیم. بدین طریق میتوان برای متغیر وابسته، پیشبینی انجام داد. در مجموعه دادههای دبیرستان، فرض کنید میخواهیم وجود رابطه خطی بین نمرات خوانش (به عنوان متغیر مستقل) و نمرات نوشتاری (متغیر وابسته) را بررسی کنیم. نتایج رگرسیون خطی ساده برای این مثال در SPSS عبارت است از:
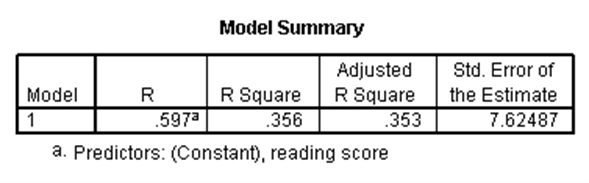
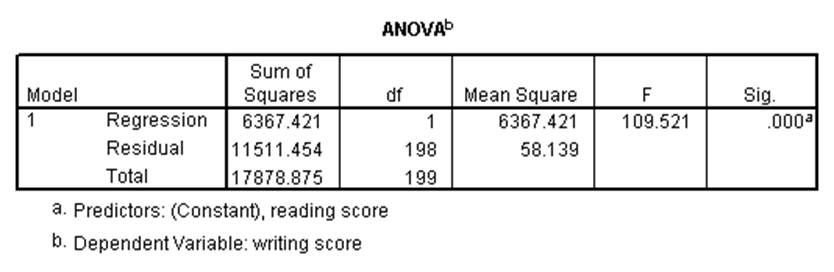
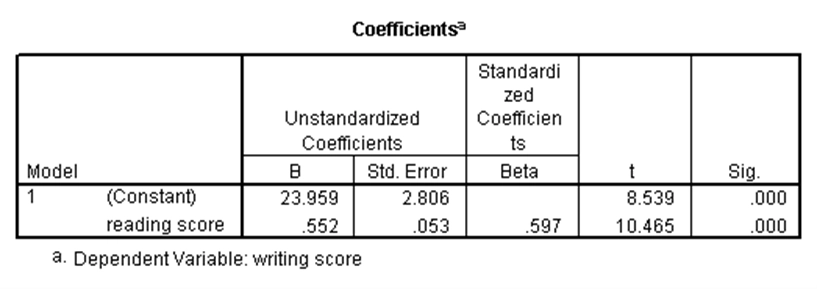
در جدول اول، اطلاعات مختلفی درباره معادله رگرسیونی ارائه شده است. در جدول دوم میتوان معنیداری کلی رگرسیون را بررسی کرد. با توجه به p-مقدار این جدول که کوچکتر از ۰.۰۵ است نتیجه میشود این رگرسیون به طور کلی معنیدار است. در جدول سوم، معنیداری هر یک از اجزای حاضر در رگرسیون قابل بررسی است. با توجه به آن که در این جدول برای جمله ثابت و متغیر خوانش، p-مقدارها کوچکتر از ۰.۰۵ هستند، حضور هر دو جمله در رگرسیون معنیدار است.
جهت مشاهده ویدیو آموزشی کلیک کنید.
برچسب ها:
- تحلیل آماری
- نرم افزار-SPSS


دیدگاه بگذارید