رگرسیون لجستیک چیست؟-فرمول ها و فرمان های آن در SPSS

رگرسیون لجستیک یکی از انواع رگرسیون است که در این مطلب ابتدا به مفهوم آن با مثالی ساده پرداخته ایم. در رگرسیون لجستیک در SPSS را دنبال خواهیم کرد. قبل از هز چیزی بهتر است که به مطلب رگرسیون سری بزنید و مفهوم آن را دریافت کنید.

رگرسیون لجستیک به زبان ساده

رگرسیون لجستیک تکنیکی آماری است برای نشان دادن تاثیر متغیرهای کمی یا کیفی بر متغیر وابسته دو وجهی (دو طبقه ای). تحلیل رگرسیون لجستیک شبیه تحلیل رگرسیون خطی است ولی با این تفاوت که در رگرسیون خطی متغیر وابسته متغیری کمی است اما در رگرسیون لجستیک متغیر وابسته متغیری کیفی و دو وجهی است. در رگرسیون لجستیک نیز متغیرهای مستقل کیفی یا باید متغیری دو وجهی باشند یا به متغیر ظاهری دو وجهی تبدیل شوند.

در رگرسیون لجستیک که متغیر وابسته متغیری وابسته متغیری دو وجهی است تاثیر متغیرهای مستقل بر آن به صورت نقش هر متغیر مستقل بر احتمال وقوع یک طبقه خاص متغیر وابسته نشان داده می‌شود

رگرسیون لجستیک یکی از خدمات تحلیل آماری است که شما می توانید آن را خود انجام دهید یا به یک شرکت آماری بسپارید، اگر وقت لازم را دارید می توانید در این مطلب کامل یک مثال ملمویس را حل کردیم که کامل آموزش ببینید، اما چنانچه وقت کافی ندارید می توانید این نوع رگرسیون را به عنوان یکی از خدمات تحلیل آماری با تعریف پروژه آماری از بخش خدمات سفارش دهید.

معادله رگرسیون لجستیک

در رگرسیون لجستیک احتمال وقوع یک طبقه خاص متغیر وابسته که اصطلاحا احتمال وقوع رویداد خوانده می‌شود بر اساس تابع نمایی متغیرهای مستقل برآورد می‌شود:

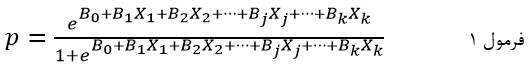
که در آن p احتمال وقوع رویداد مورد نظر است و e ثابت نپر که پایه لگاریتم طبیعی است (تقریباً معادل 718281828459047/2) و X_j متغیر مستقل jام و b_j ضریب رگرسیون لجستیک متغیر مستقل و b₀ عرض از مبدا (مقدار ثابت). به تابع:

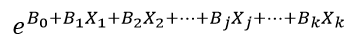
تابع نمایی می‌گویند که پایه آن عدد ثابت نپر با نماد e است و توان آن ترکیبی است خطی از متغیرهای مستقل.

همانگونه که تابع رگرسیون خطی بر اساس روش حداقل مجذورات متغیر وابسته را با کمترین خطا پیش بینی می‌کند در رگرسیون لجستیک تابع نمایی بر اساس روش لاکلیهود ماکزیمم (Maximum Likelihood) احتمال وقوع رویداد را با کمترین خطا برآورد می‌کند. لاکلیهود ماکزیمم که درستنمایی بیشینه هم ترجمه شده است روشی آماری است برای برآورد پارامتر که در آن ضرایب b متغیرهای مستقل بر اساس رسیدن به محتمل‌ترین نتایج برآورده می‌شود.

برای سادگی تفسیر ضرایب رگرسیون لجستیک معادله فوق به صورت نسبت احتمالات (Probablities Ratio) متغیر وابسته با نماد odds بیان می‌شود که عبارت است از نسبت احتمال وقوع رویداد به احتمال عدم وقوع آن:

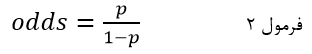
که در آن p احتمال وقوع رویداد (احتمال وقوع یک طبقه خاص متغیر وابسته) است و 1-p احتمال عدم وقوع رویداد. احتمال وقوع یک طبقه خاص متغیر وابسته (احتمال وقوع رویداد) به صورت ساده عبارت است از نسبت تعداد آن طبقه به تعداد کل:

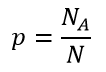
که در آن N_A تعداد عنصرهای طبقه‌ای خاص (A) است و N تعداد کل عنصرها. به عنوان مثال اگر از کل 21 نفر زن 6 نفر در انتخابات شرکت کرده باشند بنابراین احتمال شرکت در انتخابات زنان عبارت است از:

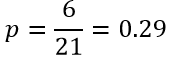
در فرمول 2 با جایگزینی p با معادلش در فرمول 1 و ساده کردن آن نسبت احتمالات متغیر وابسته به صورت تابع نمایی مجموعه‌ای از متغیرهای مستقل ارائه می‌شود:

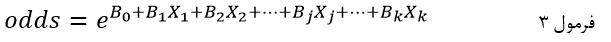
که در آن e ثابت نپر است که پایه لگاریتم طبیعی است و X_j متغیر مستقل jام و b_j ضریب رگرسیون لجستیک متغیر مستقل X_j و b₀ عرض از مبدا (مقدار ثابت).

این معادله رگرسیون لجستیک مبین آن است که نسبت احتمالات متغیر وابسته (طرف چپ معادله) تابعی است از e به توان ترکیب خطی متغیرهای مستقل (طرف راست معادله).

تعریف 1: رگرسیون لجستیک تکنیکی است برای نشان دادن تاثیر متغیرهای مستقل کمی و کیفی در احتمال وقوع متغیر وابسته دو وجهی.

ضریب b هر متغیر مستقل کمی X نشان می‌دهد در یک رگرسیون لجستیک معین با کنترل متغیرهای مستقل دیگر به ازای یک واحد تغییر در آن متغیر مستقل کمی نسبت احتمالات متغیر وابسته به چه نسبتی تغییر می‌کند. در مورد متغیر مستقل دو وجهی هم نشان می‌دهد نسبت احتمالات در یک طبقه متغیر مستقل دو وجهی به چه نسبتی با مقدار آن در طبقه دیگر تفاوت دارد.

تعریف 2: نسبت احتمالات عبارت است از نسبت احتمال وقوع رویداد به احتمال عدم وقوع آن.

ضریب b₀ که عرض از مبدا رگرسیون خطی نماست نشان می دهد که در یک رگرسیون لجستیک معین اگر مقدار همه متغیرهای مستقل صفر باشد نسبت احتمالات متغیر وابسته چقدر است.

با توجه به توضیحات فوق به بیان ساده‌تر معادله رگرسیون لجستیک عبارت است از:

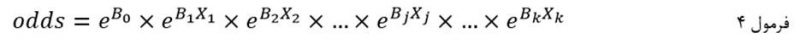
در این فرمول نسبت احتمالات متغیر وابسته تابعی است از حاصل ضرب e به توان ضریب b₀ (عرض از مبدا رگرسیون خطی متغیرهای مستقل) در e به توان هر یک از متغیرهای مستقل ضرب در ضریب رگرسیون لجستیک‌اش (b).

حال برای نشان دادن مفهوم رگرسیون لجستیک از یک مثال ساده استفاده می‌کنیم.

مثال 1: گیریم محققی با این استدلال که هر چه جایگاه اجتماعی افراد جامعه بالاتر باشد توجه شان به جامعه بیشتر خواهد بود فرض کرده است که میزان مشارکت مردان (که جایگاه اجتماعی بالاتری دارند) در انتخابات بیشتر از زنان است و همچنین هرچه تحصیلات افراد بالاتر باشد (که جایگاه اجتماعی بالاتری دارند) احتمال مشارکت آنها در انتخابات بیشتر می‌شود.

محقق مذکور طی مصاحبه‌ای با نمونه ای تصادفی از افراد یک شهر مشارکتشان در انتخابات گذشته را جویا شده و تحصیلات آنها را هم پرسیده و جنسیتشان را نیز یادداشت کرده است.

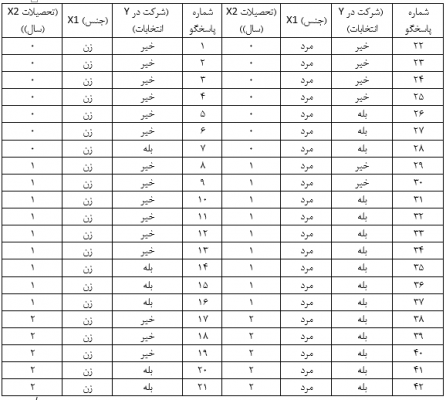
در این مثال نسبت احتمالات شرکت زنان در انتخابات (odds_f) با فرمول 2 عبارت است از:

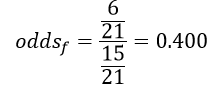
و نسبت احتمالات شرکت مردان در انتخابات (odds_m):

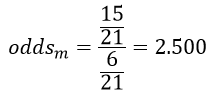
به این ترتیب می‌بینیم که نسبت احتمالات شرکت مردان در انتخابات بسیار بیشتر از نسبت احتمالات شرکت زنان در انتخابات است:

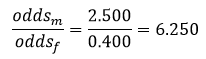
نسبت احتمالات شرکت مردان در انتخابات 25/6 برابر نسبت احتمالات شرکت زنان در انتخابات است.

حال اگر متغیر جنس (X1) را به صورت صفر و ۱ کدگذاری کنیم (صفر برای زن و یک برای مرد) و متغیر شرکت در انتخابات (Y) را هم به صورت صفر و ۱ کدگذاری کرده (1 برای شرکت در انتخابات و صفر برای عدم شرکت) و داده‌ها را وارد فایل SPSS کنیم با اجرای فرمان رگرسیون لجستیک متغیر وابسته شرکت در انتخابات (Y) با متغیر مستقل جنس (X1) ضرایب رگرسیون لجستیک جنس و ثابت آن در نمای e به صورت جدول زیر ارائه خواهد شد.

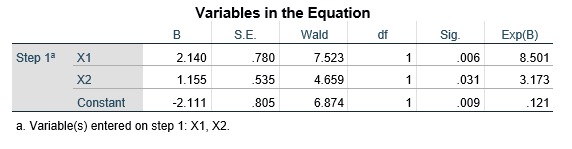
با قرار دادن ضرایب جدول فوق در فرمول 4 نسبت احتمالات متغیر وابسته شرکت در انتخابات (Y) بر حسب متغیر مستقل جنس (X1) به این قرار می‌شود:

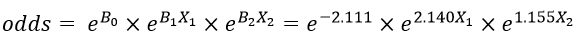
مقدار ضریب b₀ مبین آن است که در این رگرسیون لجستیک در جایی که مقدار متغیر مستقل جنس (X1) و تحصیلات (X2) هر دو صفر است نسبت احتمالات متغیر وابسته به شرکت در انتخابات (Y) معادل e^-2.111 است که برابر 121/0 می‌‌شود. به عبارت دیگر مقدار ضریب b₀ نشان می‌دهد که نسبت احتمال مشارکت زنان بیسواد در انتخابات به احتمال عدم مشارکتشان 121/0 است.

ضریب b متغیر مستقل جنس (X1) نشان می‌دهد در این رگرسیون لجستیک با کنترل متغیرهای مستقل دیگر نسبت احتمالات شرکت مردان در انتخابات e^2.140 برابر است. به عبارت دیگر با در نظر گرفتن تحصیلات نسبت احتمالات شرکت مردان در انتخابات 501/8 برابر نسبت احتمالات شرکت زنان در انتخابات است در مورد مردان از آنجا که X1=1 آنگاه:

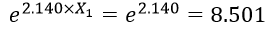
ضریب b متغیر مستقل تحصیلات (X2) حاکی است با کنترل متغیر مستقل دیگر به ازای یک سال افزایش در تحصیلات نسبت احتمالات متغیر وابسته e^1.155 برابر یا معادل 173/3 برابر می‌شود. اگر X2 معادل یک باشد آنگاه:

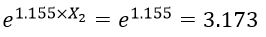
خواهد شد. به عبارت دیگر با در نظر گرفتن جنسیت افراد با یک سال افزایش تحصیلات نسبت احتمال شرکت در انتخابات به عدم شرکت در آن 173/3 برابر می‌شود.

به این ترتیب تحلیل رگرسیون لجستیک نشان می‌دهد هر دو فرضیه مثال 1 تایید می‌شود: هم میزان مشارکت مردان در انتخابات بیشتر از زنان است و هم با افزایش تحصیلات بر میزان مشارکت در انتخابات افزوده می‌شود.

در رگرسیون لجستیک نیز تقریباً مانند رگرسیون خطی متغیرهای مستقل همبسته در هر زیرمجموعه متفاوتی از متغیرهای مستقل ضرایب رگرسیون آنها تغییر می‌کند زیرا در احتساب ضریب رگرسیون هر متغیر مستقل اثر سایر متغیرهای مستقل به حساب آمده و به گونه‌ای احتساب می‌شود که خطای پیش بینی احتمال به حداقل ممکن برسد.

کاربرد رگرسیون لجستیک

کاربرد اصلی تحلیل رگرسیون لجستیک برای نشان دادن تاثیر مجموعه‌ای از متغیرهای مستقل بر متغیر وابسته است. کاربرد دیگر آن برای پیش بینی مقدار متغیر وابسته هر عنصر بر اساس وضعیت آن عنصر در متغیرهای مستقل است. مثلاً پیش‌بینی می‌کنیم کسی بر اساس وضعیت جسمانی‌اش در مجموعه‌ای از عوامل (متغیرهای مستقل) موثر بر یک بیمار خاص به آن بیماری مبتلاست یا نه. یا فردی بر اساس وضعیت خویش در مجموعه‌ای از عوامل (متغیرهای) موثر بر مشارکت در انتخابات رأی می‌دهد یا خیر.

تاثیر متغیرهای مستقل

هرگاه ضریب b یک متغیر مستقل صفر نبود (b ≠ 0) و در جایی که داده‌ها از نمونه‌ای احتمالی از جمعیتی بزرگ به دست آمده باشد سطح معناداری ضریب b معادل 05/0 یا کمتر از آن بود (Sig ≤ 0.05) بدان معناست که متغیر مستقل در متغیر وابسته یا به بیان دقیق تر در نسبت احتمالات متغیر وابسته نقش دارد.

در جایی که ضریب b متغیر مستقل مثبت باشد تابع نمایی آن (e به توان آن ضریب) از یک بیشتر می‌شود و حاکی از اثر متغیر مستقل در افزایش نسبت احتمالات و احتمال وقوع رویداد (احتمال وقوع یک طبقه خاص متغیر وابسته) است.

درجایی که ضریب b متغیر مستقل منفی باشد تابع نمایی آن از یک کمتر می‌شود و حاکی از اثر متغیر مستقل در کاهش نسبت احتمالات و احتمال وقوع رویداد است.

اما اگر ضریب b یک متغیر مستقل صفر بود تابع نمایی آن مساوی یک می‌شود (e⁰ = 1) و نقشی در افزایش یا کاهش نسبت احتمالات و احتمال وقوع رویداد ندارد.

نکته 1: ضریب b مثبت حاکی از اثر متغیر مستقل در افزایش نسبت احتمالات و احتمال وقوع رویداد است و ضریب منفی b حاکی از اثر متغیر مستقل در کاهش نسبت احتمالات.

پیش بینی متغیر وابسته

برای پیش بینی وضعیت هر عنصر در متغیر وابسته و مقادیر متغیرهای مستقل آن عنصر را در معادله رگرسیون قرار می‌دهیم تا نسبت احتمالات عنصر مشخص شود.

اگر نسبت به احتمالات عنصر مورد نظر از یک بیشتر باشد:

odds > 1

احتمال وقوع رویداد برای آن عنصر بزرگ‌تر از 50/0 است

اگر:

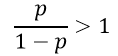
آنگاه:

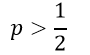
در این صورت پیش بینی می‌کنیم رویداد برای آن عنصر به وقوع می‌پیوندد (آن عنصر در طبقه مورد نظر قرار می‌گیرد).

به عنوان مثال بر اساس معادله رگرسیون لجستیک مثال 2 نسبت احتمالات پاسخگوی شماره 31 جدول که مرد است (X1=1) و تحصیلاتش یک سال است (X2=1) معادل:

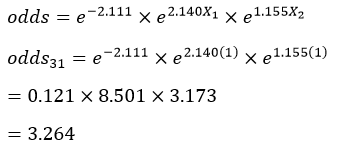
می‌شود که چون بزرگتر از یک است و احتمال وقوع رویداد (شرکت در انتخابات) برای آن عنصر بزرگتر از 50/0 است پیش بینی می‌کنیم رویداد مورد نظر برای آن عنصر به وقوع می‌پیوندد (یا اگر مربوط به گذشته بوده به وقوع پیوسته است).

اگر نسبت احتمالات عنصر مورد نظر از یک کمتر باشد:

odd < 1

احتمال وقوع رویداد برای آن عنصر کمتر از 50/0 است:

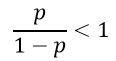
در نتیجه:

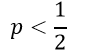
در این صورت پیش بینی می‌کنیم رویداد مورد نظر برای آن عنصر به وقوع نمی‌پیوندد.

به عنوان مثال بر اساس معادله رگرسیون لجستیک مثال 2 نسبت احتمالات پاسخگوی شماره 9 جدول که زن است (X1=0) و تحصیلاتش یک سال است (X2=1) معادل:

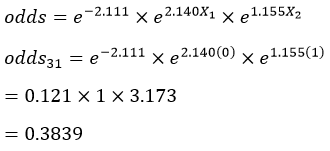
می‌شود که چون کوچک‌تر از یک است و احتمال وقوع رویداد (شرکت در انتخابات) برای آن عنصر کمتر از 50/0 است پیش‌‌بینی می‌کنیم رویداد مورد نظر برای آن عنصر به وقوع نمی‌پیوندد (یا اگر مربوط به گذشته است به وقوع نپیوسته است).

اما اگر نسبت احتمالات معادل یک باشد:

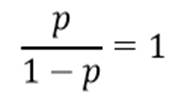
احتمال وقوع رویداد معادل 50/0 است:

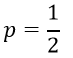
در این صورت احتمال وقوع رویداد با احتمال عدم وقوع آن برابر می‌شود و فرقی نمی‌کند که کدام حالت برای عنصر مورد نظر پیش بینی شود. از این رو معمولاً وقوع رویداد را پیش بینی می‌کنند.

احتمال وقوع رویداد برای هر عنصر را می‌توان از نسبت احتمالات تقسیم بر یک به اضافه نسبت احتمالات به طور دقیق به دست آورد:

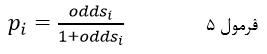
که در آن p_i احتمال وقوع رویداد برای عنصر iام و odds_i نسبت احتمالات برای آن عنصر.

فرمول 5 همان فرمول 1 است که بر اساس فرمول 3 نسبت احتمالات (odds) جایگزین تابع نمایی شده است.

به عنوان مثال احتمال وقوع رویداد برای پاسخگوی شماره ۳۱ عبارت است از:

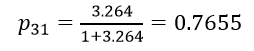
و احتمال وقوع رویداد برای پاسخگوی شماره ۹:

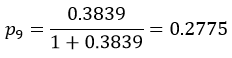
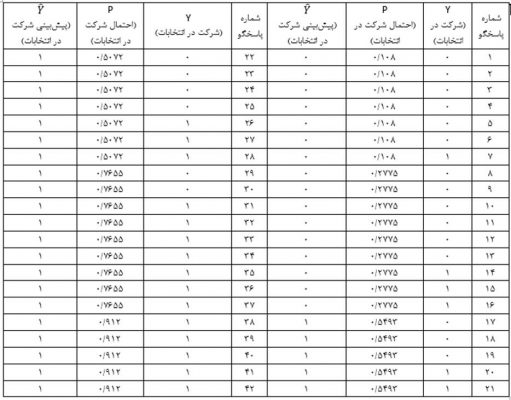
احتمال وقوع رویداد برای تک تک پاسخگویان عنصرهای مثال 2 و پیش بینی وقوع رویداد (شرکت در انتخابات با کد ۱) یا عدم وقوع آن (عدم شرکت در انتخابات با کد صفر) برای آنها در جدول زیر ارائه شده است.

نرم افزار SPSS به عنوان یکی از پر کاربرد ترین نرم افزار های آماری شناخته می شود،دوره آموزش نرم افزار SPSS یک دوره کامل که با مثال های کاربردی تمامی مباحث کاربردی در نرم افزار را گام به گام آموزش میدهد،علاوه بر این از پشتیبانی خیلی خوبی برای انجام پروژه برخوردار است.یک فرصت اشتغال خوب نیز در پروژه های آماری برای مهارت آموزان فراهم خواهد شد

رگرسیون لجستیک در SPSS

برای اجرای فرمان رگرسیون لجستیک بعد از وارد کردن داده ها به فایل SPSS و تعریف آنها در بخش تحلیل Analyze در قسمت رگرسیون Regression قسمت لجستیک دووجهی Binary Logistic… را کلیک می‌کنیم. قبل آن شاید دوست داشته بدانید نرم افزار spss چیست؟

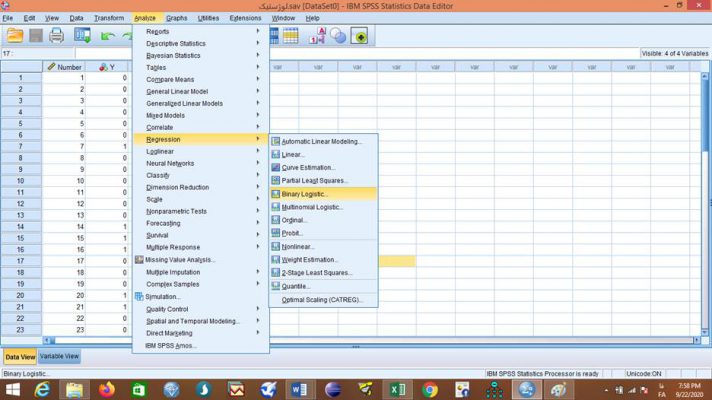
با باز شدن صفحه رگرسیون لجستیک Logistic Regression متغیر وابسته را از بین متغیرهای خانه سمت چپ انتخاب می‌کنیم و به خانه متغیر وابسته Dependent انتقال می‌دهیم. همینطور متغیر یا متغیرهای مستقل مورد نظر را به خانه متغیرهای هم تغییر Covariates منتقل کرده و فرمان را تایید OK می‌کنیم.

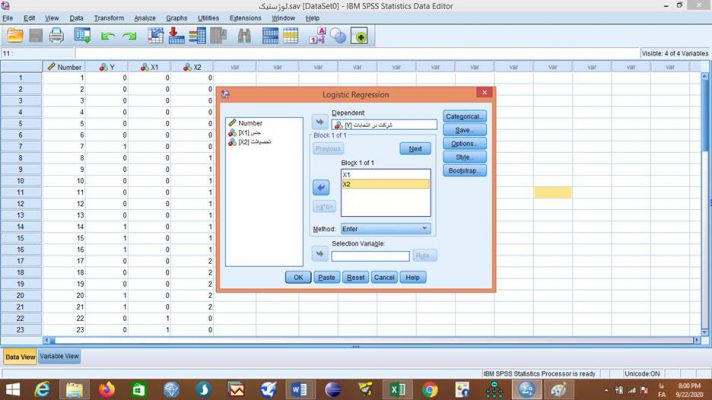
جدول‌های رگرسیون لجستیک

با اجرای فرمان رگرسیون لجستیک جدول‌های متعددی ارائه می‌شود. چند جدول اول توصیف متغیرها از لحاظ تعداد عنصرها و نحوه کدگذاری متغیر وابسته دو وجهی و متغیرهای کیفی است. جدول‌های قسمت بعدی زیر عنوان بلوک صفر (Block0) می‌آیند. بلوک صفر مرحله آغازین (مرحله صفر) تحلیل رگرسیون لجستیک که متغیرهای مستقل وارد تحلیل نشده اند و فقط ثابت (Constant) تحلیل می‌شود.

جدول‌های قسمت بعدی زیر عنوان بلوک یک (Block1) قرار دارند. بلوک ۱ اولین مرحله تحلیل رگرسیون لجستیک است که متغیرهای مستقل را در بر می‌گیرد.

در اینجا این جدول‌ها را با اجرای فرمان رگرسیون لجستیک متغیر وابسته شرکت در انتخابات (Y) با دو متغیر مستقل جنس (X1) و تحصیلات (X2) داده‌های جدول مثال 2 شرح می‌دهیم.

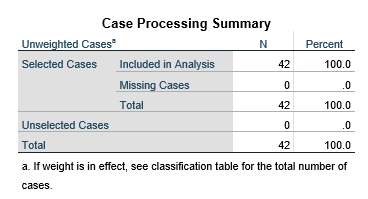
جدول خلاصه پردازش عنصرها

جدول خلاصه پردازش عنصرها Case Processing Summary مانند جدول زیر گزارشی است درباره تعداد عنصرهای مشمول تحلیل و عنصرهای نامشخص و عنصرهای انتخاب نشده و کل عنصرها.

به عنوان مثال در این جدول می‌بینیم که تعداد عنصرهای مشمول تحلیل معادل ۴۲ عنصر که ۱۰۰ درصد عنصرهاست. هیچ عنصر نامشخص وجود ندارد. هیچ عنصر انتخاب نشده هم در بین نیست و تعداد کل عنصرها هم ۴۲ عنصر است.

جدول کدگذاری متغیر وابسته

جدول کدگذاری متغیر وابسته Dependent Variable Encoding مانند جدول زیر نحوه کدگذاری صفر و یک متغیر وابسته دو وجهی را نشان می‌دهد. فرمان رگرسیون لجستیک به طبقه اول متغیر وابسته به عنوان عدم وقوع رویداد کد صفر و به طبقه دوم به عنوان وقوع رویداد کد یک می‌دهد مانند جدول که به طبقه اول (خیر) کد صفر و به طبقه دوم (بله) کد یک داده است. ستون اول (Original Value) جدول کدگذاری متغیر وابسته به کد اولیه متغیر اختصاص دارد و ستون دوم (Internal Value) به کد جدید متغیر.

اگر بین متغیرهای مستقل متغیر دو وجهی یا متغیر ظاهری وجود داشته باشد که تحت عنوان متغیر طبقه‌ای در فرمان رگرسیون لجستیک مشخص شده باشد جدول یا جدول‌های نحوه کدگذاری صفر و یک آنها نیز ارائه می‌شود.

جدول‌های بلوک صفر

جدول‌هایی که زیر عنوان بلوک صفر: بلوک آغازین Block0: Beginning Block می‌آیند جدول‌های تحلیل رگرسیون لجستیک است که فقط ضریب ثابت را در بر می‌گیرد و مراحل بعدی تحلیل با آن مقایسه می‌شود.

جدول طبقه بندی

جدول طبقه بندی Classification Table مانند جدول زیر شامل تعداد عنصرهای مشاهده شده در هر طبقه متغیر وابسته و تعداد عنصرهای پیش بینی شده است. تعداد عنصرهای مشاهده شده در سطرهای جدول می‌آید. در جدول زیر می‌بینیم که در سطر اول تعداد عنصرهای مشاهده شده مثال 2 در طبقه “خیر” ۲۱ عنصر و در سطر دوم تعداد عنصرهای طبقه “بله” هم ۲۱ عنصر است.

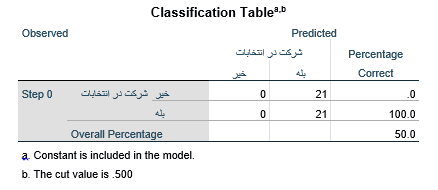
تعداد عنصرهای پیش بینی شده هم در ستون‌های جدول می‌آید. در مرحله اول تحلیل رگرسیون لجستیک (بلوک صفر) پیش بینی عضویت طبقاتی عنصرها بر اساس احتمال وقوع رویداد به دست می‌آید که عبارت است از نسبت تعداد عنصرهای طبقه مورد نظر (طبقه با کد ۱) به کل عنصرها:

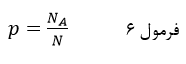
که در آن p احتمال وقوع رویداد (احتمال تعلق داشتن به طبقه مورد نظر در متغیر وابسته) است و N_A تعداد عنصرهای آن طبقه مورد نظر و N تعداد کل عنصرها.

به عنوان مثال در جدول داده‌ها که تعداد عنصرهای طبقه “خیر” ۲۱ نفر است و تعداد کل عنصرها ۴۲ نفر احتمال کلی وقوع رویداد (شرکت در انتخابات) عبارت است از:

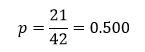
هرگاه احتمال کلی وقوع رویداد معادل 500/0 یا بزرگ‌تر بود (p ≥ 0.500) فرمان رگرسیون لجستیک همه عنصرها را متعلق به طبقه وقوع رویداد پیش بینی می‌کند مانند همین مثال که احتمال کلی وقوع رویداد معادل 500/0 است و پیش‌بینی می‌شود همه پاسخگویان (عنصرها) در انتخابات شرکت کرده اند. در نتیجه همان طور که در ستون آخر جدول طبقه‌بندی می‌بینیم درباره ۲۱ پاسخگوی مثال 2 که در انتخابات شرکت نکرده اند پیش‌بینی شده است همه شرکت کرده‌اند.

این بدان معناست که هیچ یک از این عنصرها درست پیش‌بینی نشده است (درصد پیش‌بینی صحیح صفر است). درباره ۲۱ پاسخگویی که در انتخابات شرکت کرده‌اند پیش‌بینی شده همه شرکت کرده‌اند. این بدان معناست که ۱۰۰درصد پیش‌بینی صحیح است. درصد پیش بینی کل عنصرها هم عبارت است از:

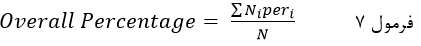
که در آن per_i درصد پیش‌بینی صحیح عنصرهای طبقه iام است از و N_i تعداد عنصرهای طبقه iام و N تعداد کل عنصرها.

درصد پیش‌بینی کل عنصرها در این مثال ۵۰ درصد می‌شود:

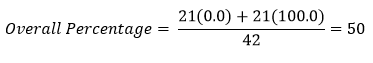
جدول متغیرهای معادله

جدول متغیرهای معادله Variables in the Equation بلوک صفر مانند جدول زیر آماره‌های ثابت (Constant) را بیان می‌کند. در ستون اول درج شده است که این مرحله مرحله صفر (Step0) تحلیل است. ستون دوم (ستون B) مقدار ضریب ثابت (Constant) را نشان می‌دهد که توان تابع نمایی e^B این مرحله است.

ستون سوم به خطای استاندارد (S.E.) ضریب ثابت اختصاص دارد که برای برآورد پارامتر (ضریب ثابت) در جمعیت مبنای نمونه گیری احتمالی است. ستون چهارم به آماره والد (Wald) اختصاص دارد که آزمون آماری فرضیه صفر (H₀) ضریب ثابت مبنی بر صفر بودن ضریب ثابت در جمعیت است‌.

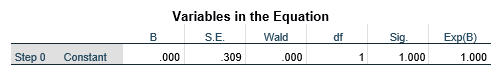
ستون بعدی درجه آزادی (df) آزمون والد را نشان می‌دهد که معادل تعداد پارامترهاست. ستون بعدی سطح معناداری (Sig) آزمون والد را نشان می‌دهد. در این مثال که سطح معناداری یک است بدان معناست که تحت فرضیه صفر (H₀) احتمال رسیدن به ضریب ثابت مشاهده شده صد در صد است و لاجرم فرضیه صفر (H₀) رد نمی‌شود. ستون آخر مقدار تابع نمایی این مرحله را که e^B است نشان می‌دهد.

در این مثال که ضریب ثابت صفر است تابع نمایی معادل یک می‌شود (e⁰ = 1). مقدار تابع نمایی این مرحله مبین نسبت احتمالات متغیر وابسته بدون در نظر گرفتن متغیرهای مستقل است.

این آماره‌ها در جدول متغیرهای معادله مرحله ۱ که در ادامه به میان می‌آید با تفصیل بیشتری عنوان می‌شود.

جدول متغیرهای بیرون معادله

جدول متغیرهای بیرون معادله  در بلوک صفر مبین مجموعه متغیرهای مستقل است که در این مرحله وارد تحلیل رگرسیون لجستیک نشده‌اند و در مرحله بعد وارد می‌شوند مانند جدول زیر که نشان می‌دهد در این مثال دو متغیر X1 و X2 وارد تحلیل نشده‌اند.

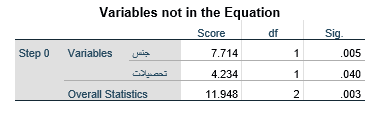
ستون نمره (Score) مقدار آزمون آماری هر متغیر مستقل بیرون از مدل صفر است که عبارت است از منهای دو لگاریتم نسبت لاکلیهود (-2LL). نسبت لاکلیهود نیز لاکلیهود مدل صفر تقسیم بر لاکلیهود مدل با ورود آن متغیر است. این آزمون آماری دارای توزیع کی دو با درجه آزادی (df) معادل تفاضل تعداد ضریب رگرسیون لجستیک دو مدل است.‌ به عنوان مثال در جدول فوق می‌بینیم چنانچه متغیر مستقل X1 وارد مدل رگرسیون لجستیک شود دارای یک ضریب رگرسیون بیشتر از مدل صفر می‌شود و از این رو درجه آزادی معادل یک است.

سطح معناداری (Sig) آزمون مذکور نشان می‌دهد ورود متغیر به مدل معنادار است یا نه. به عنوان مثال در جدول فوق می‌بینیم چنانچه متغیر مستقل X1 وارد مدل رگرسیون لجستیک شود سطح معناداری آزمون آماری آن کمتر از 05/0 و در نتیجه معنادار است. این به معنای رد فرضیه صفر مبنی بر معادل صفر بودن مقدار ضریب رگرسیون این متغیر در جمعیت کل است.

جدول‌های بلوک ۱

جدول‌های قسمت بعدی زیر عنوان بلوک ۱: روش …(Block1: Method = …) قرار دارند. بلوک ۱ اولین مرحله بعدی تحلیل رگرسیون لجستیک است که متغیرهای مستقل را در بر می‌گیرد و روش رگرسیون لجستیک نیز مشخص می‌شود.

جدول آزمون کلی ضرایب مدل

جدول آزمون کلی ضرایب مدل Omnibus Tests of Model Coefficients نشان می‌دهد با فرود متغیرهای مستقل لگاریتم لاکلیهود مدل نسبت به مدل قبلی کاهش معنادار (قابل تعمیم به جمعیت) پیدا می‌کند یا نه.

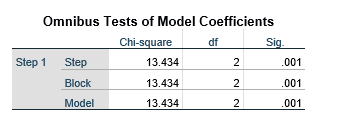
ستون اول نشان می‌دهد تحلیل در چه مرحله ای است. ستون دوم و ستون کی‌دو (Chi-square) مبین مقدار کاهش منهای دو لگاریتم لاکلیهود (-2LL) این مرحله نسبت به مرحله قبل است. هرچه این تغییر بیشتر باشد نقش متغیرهای مستقل مدل در تغییر نسبت احتمالات متغیر وابسته بیشتر است.

ستون بعدی درجه آزادی (df) این تغییر را نشان می‌دهد. درجه آزادی سطر اول معادل تفاضل تعداد ضریب رگرسیون مرحله (Step) جاری از مرحله قبلی است. درجه آزادی سطر دوم هم معادل تفاضل تعداد ضریب رگرسیون بلوک (Block) جاری از بلوک قبلی است. درجه آزادی سطر سوم معادل تفاضل تعداد ضریب رگرسیون مدل (Model) جاری از مدل مرحله صفر است.

ستون بعدی سطح معناداری (Sig) این تغییر است. در این مثال سطح معناداری کمتر از 05/0 است و بدان معناست که فرضیه صفر (H₀) مبنی بر صفر بودن این تغییر در جمعیت کل رد می‌شود و تغییر مشاهده شده به جمعیت تعمیم پذیر است.

سطر اول جدول آزمون کلی ضرایب مدل شامل تغییر کی دو و درجه آزادی و سطح معناداری این مرحله (Step) نسبت به مرحله قبل است. سطر دوم جدول تغییر مذکور این بلوک (Block) را نسبت به بلوک قبل نشان می‌دهد. سطر سوم جدول هم تغییر کی‌دو این مدل (Model) را نسبت به مدل صفر (مدلی که فقط دارای ثابت است) نشان می‌دهد.

در جدول فوق مقادیر هر سه سطر یکی است زیرا در مرحله ۱ هر سه آماره مذکور با مرحله صفر مقایسه می‌شوند. در این مثال روش رگرسیون لجستیک روش ورود (Enter) است که با آن متغیرهای مستقل فقط در مرحله ۱ (Step1) وارد تحلیل رگرسیون خطی می‌شوند. اما اگر رگرسیون لجستیک با روش‌های دیگر انجام شود شامل مراحل بعدی هم خواهد بود که در آن صورت تغییر کی‌دو هر مرحله با مرحله قبل مقایسه می‌شود.

همچنین در این مثال فقط یک بلوک از متغیرهای مستقل وارد تحلیل شده بود و لاجرم تغییر این بلوک با مرحله صفر مقایسه می‌شود. حال اگر محقق مجموعه دیگری از متغیرهای مستقل را تحت عنوان بلوک ۲ به متغیرهای مستقل بلوک اول می‌افزود در گام بعدی تحلیل تغییر کی دو بلوک ۲ در مقایسه با بلوک ۱ ارائه می‌شد و الی آخر. اما تغییر کی‌دو هر مدل (Model) همواره با مدل مرحله صفر مقایسه می‌شود.

برازندگی مدل لجستیک در جدول خلاصه مدل

جدول خلاصه مدل Model Summary مانند جدول زیر آماره‌های برازندگی مدل لجستیک را نشان می‌دهد.

ستون دوم منهای دو لگاریتم لاکلیهود (-2 Log likelihood) مبین برازندگی مدل لجستیک بر اساس لاکلیهود است. لاکلیهود عبارت است از احتمال نتایج مشاهده شده بر اساس برآورد پارامتر (ضرایب رگرسیون متغیرهای مستقل). معمولا به جای لاکلیهود که مقداری کسری است منهای دو لگاریتم لاکلیهود با نماد -2LL را به عنوان میزان برازندگی مدل لجستیک به کار می‌برند.

هر چه لاکلیهود بزرگتر باشد که معادل کوچکتر شدن منهای دو لگاریتم لاکلیهود است مدل برازنده تر است. وقتی لاکلیهود یک می‌شود که معادل صفر شدن منهای دو لگاریتم لاکلیهود است برازندگی مدل لجستیک کامل است.

ستون سوم ضریب R² کاکس و اسنل (Cox & Snell R Square) مبین شاخص دیگر برازندگی مدل لجستیک است که معادل یک منهای نسبت لاکلیهود مدل مرحله صفر (مدل با ثابت) به لاکلیهود مدل مرحله آخر به توان ۲ تقسیم بر تعداد کل عنصرهاست:

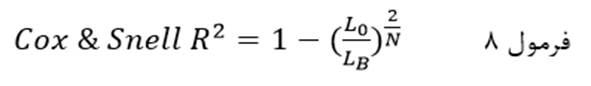
که در آن L₀ لاکلیهود مدل مرحله صفر (مدل باثابت) است و L_B لاکلیهود مدل مرحله آخر (مدل با متغیرهای مستقل) و N تعداد کل عنصرها.

حداقل ضریب R² کاکس و اسنل صفر است که بدان معناست متغیرهای مستقل هیچ نقشی بر متغیر وابسته (نسبت احتمالات آن) ندارند و مدل رگرسیون لجستیک به هیچ وجه برازندگی ندارد. در عوض هر چه نقش متغیرهای مستقل بر نسبت احتمالات متغیر وابسته بیشتر باشد و به یک نزدیکتر باشد مدل رگرسیون تطابق بیشتری با داده‌ها دارد و برازندگی آن بیشتر است. در جایی که مدل رگرسیون تطابق کاملی با داده‌ها دارد و برازندگی آن کامل است مقدار ضریب R² کاکس و اسنل به حداکثر خود می‌رسد که کمتر از یک در می‌آید اما حد معینی ندارد. از این رو برای رفع این نقص ضریب R² نگلکرک ارائه شده است.

ستون چهارم که ضریب R² نگلکرک (Nagelkerke R Square) است شاخص دیگر برازندگی مدل لجستیک است که معادل نسبت ضریب R² کاکس و اسنل به حداکثر ضریب R² کاکس و اسنل است:

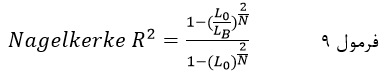
که در آن L₀ لاکلیهود مدل مرحله صفر (مدل با ثابت) است و L_B لاکلیهود مدل مرحله آخر (مدل با متغیرهای مستقل) و N تعداد کل عنصرها.

حداکثر ضریب R² کاکس و اسنل در جایی است که لاکلیهود مدل به حداکثر مقدار خود که یک است برسد     (L_B = 1). به این ترتیب دامنه ضریب R² نگلکرک صفر تا یک است و تفسیر آن هم مانند تفسیر ضریب R² کاکس و اسنل است.

تحلیل رگرسیون لجستیک درجدول طبقه بندی

جدول طبقه بندی Classification Table در مرحله بعدی تحلیل رگرسیون لجستیک شامل تعداد عنصرهای مشاهده شده در هر طبقه متغیر وابسته و تعداد عنصرهای پیش‌بینی شده بر اساس رگرسیون لجستیک است. تعداد عنصرهای مشاهده شده در سطرهای جدول می‌آید. در جدول زیر می‌بینیم که در سطر اول تعداد عنصرهای مشاهده شده در طبقه “خیر” ۲۱ عنصر (9 + 12) و در سطر دوم تعداد عنصرهای طبقه “بله” هم ۲۱ عنصر   (17 + 4) است.

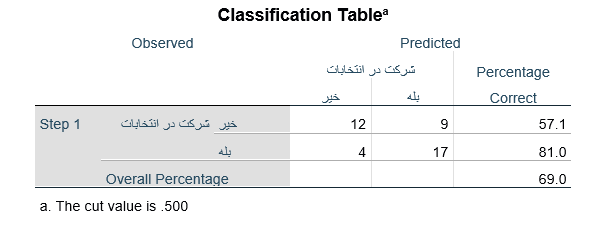
تعداد عنصرهای پیش بینی شده هم در ستون‌های جدول می‌آید. در مرحله ۱ تحلیل رگرسیون لجستیک (Step1) پیش‌بینی عضویت طبقاتی عنصرها بر اساس معادله رگرسیون لجستیک و احتساب احتمال وقوع رویداد برای هر عنصر (با فرمول 5) به دست می‌آید. هرگاه احتمال وقوع رویداد برای هر عنصر معادل 5/0 یا بزرگ‌تر بود (p_i ≥ 0.5) آن عنصر متعلق به طبقه مورد نظر پیش بینی می‌شود.

به عنوان مثال در جدول فوق درباره ۲۱ پاسخگوی مثال 2 که در انتخابات شرکت نکرده‌اند پیش‌بینی شده است ۱۲ نفر شرکت نکرده اند. این بدان معناست که 1/57 درصد پیش بینی صحیح است. درباره ۲۱ پاسخگویی که در انتخابات شرکت کرده‌اند پیش‌بینی شده است ۱۷ نفر شرکت کرده اند. این بدان معناست که ۸۱ درصد پیش بینی صحیح است.

درصد پیش بینی کل عنصرها هم بر اساس فرمول 7 عبارت است از:

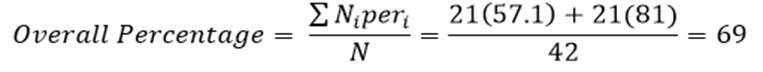
جدول متغیرهای معادله

جدول متغیرهای معادله Variables in the Equation مرحله بلوک یک تحلیل رگرسیون لجستیک شامل مجموعه متغیرهای مستقل و ثابت (Constant) بوده و آماره‌های آن را بیان می‌کند. جدول متغیرهای معادله جدول اصلی رگرسیون لجستیک است و برای تحلیل نتایج کافی است. در ستون اول این جدول نام مراحل رگرسیون لجستیک و متغیرهای مستقل آن مرحله ارائه می‌شود مانند جدول زیر که مرحله یک (Step1) درج شده است. در روش ورود (Enter) همواره بعد از مرحله صفر (Step0) همین مرحله یک وجود دارد که شامل همه متغیرهای مستقل است.

ستون دوم (ستون B) به ضرایب رگرسیون لجستیک متغیرهای مستقل و ثابت اختصاص دارد. همانطور که پیشتر به میان آمد ضریب رگرسیون لجستیک b هر متغیر مستقل X نشان می‌دهد با کنترل متغیرهای مستقل دیگر به ازای یک واحد تغییر در آن متغیر نسبت احتمالات متغیر وابسته (odds) به نسبت e به توان آن ضریب رگرسیون لجستیک (e^b) تغییر می‌کند. ضریب ثابت (Constant) هم نشان می‌دهد اگر مقدار همه متغیرهای مستقل صفر باشد نسبت احتمالات متغیر وابسته e به توان آن ضریب ثابت است. ستون آخر (Exp(B)) هم مقدار e به توان هر ضریب رگرسیون لجستیک را نشان می‌دهد.

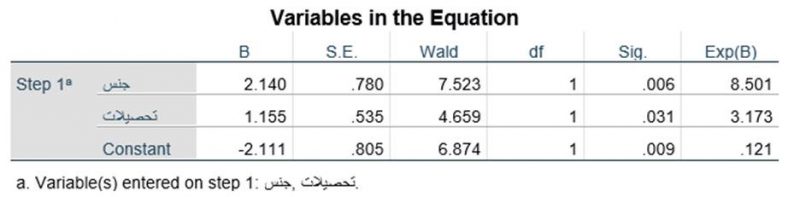
به عنوان مثال در جدول فوق مقدار ضریب رگرسیون لجستیک متغیر مستقل کمی تحصیلات (X2) که 155/1 است حاکی است با کنترل متغیر X1 به ازای یک سال افزایش در تحصیلات نسبت احتمالات متغیر وابسته (odds) به نسبت e^1.155 تغییر می‌کند که با توجه به ستون آخر این تغییر معادل 173/3 است. به عبارت دیگر مقدار ضریب b متغیر مستقل کمی تحصیلات حاکی است با یک سال افزایش در تحصیلات نسبت احتمالات مشارکت در انتخابات 173/3 برابر می‌شود.

یا مقدار ضریب b متغیر مستقل دووجهی جنس (X1) مبین آن است که با کنترل متغیر تحصیلات (X2) در طبقه کد یک متغیر جنس (مرد) در مقایسه با طبقه کد صفر (زن) نسبت احتمالات متغیر وابسته به نسبت e^2.140 تغییر می‌کند که با توجه به ستون آخر این تغییر معادل 501/8 است. به عبارت دیگر مقدار ضریب b متغیر مستقل جنس حاکی است نسبت احتمالات مشارکت در انتخابات مردان 501/8 برابر نسبت احتمالات مشارکت در انتخابات زنان است.

مقدار ضریب ثابت هم نشان می‌دهد اگر مقدار متغیرهای مستقل X1 و X2 صفر باشد (در این مثال پاسخگویان زن و بیسواد باشند) نسبت احتمالات متغیر وابسته معادل e^-2.111 است که با توجه به ستون آخر معادل 121/0 است. به عبارت دیگر مقدار ضریب ثابت حاکی است نسبت احتمالات مشارکت در انتخابات زنان بیسواد 121/0 است.

ستون سوم به خطای استاندارد (S.E.) ضریب رگرسیون متغیرهای مستقل اختصاص دارد که برای برآورد پارامتر (ضریب رگرسیون) در جمعیت مبنای نمونه گیری احتمالی است.

ستون چهارم به آماره والد (Wald) اختصاص دارد که آزمون آماری ضریب رگرسیون لجستیک هر یک از متغیرهای مستقل مدل است و مجذور نسبت ضریب رگرسیون لجستیک متغیر مستقل بر خطای استانداردش است:

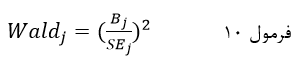
که در آن B_j ضریب رگرسیون لجستیک متغیر مستقل X_j است و SE_j خطای استاندارد ضریب B_j.

به عنوان مثال مقدار آماره والد ضریب رگرسیون لجستیک متغیر جنس (X1) مثال 2 عبارت است از:

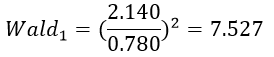
که معادل مقداری است که در جدول فوق آمده است (تفاوت ناچیز ناشی از خطای گرد کردن است).

تحت فرضیه صفر یعنی اگر مقدار ضریب رگرسیون لجستیک متغیر مستقل در جمعیت مبنای نمونه‌گیری صفر باشد آماره والد یک متغیر دارای توزیع کی دو با درجه آزادی یک است. درجه آزادی آماره متغیر کیفی معادل تعداد طبقات منهای یک است. هر جا که سطح معناداری والد مساوی 05/0 یا کمتر از آن شد (Sig ≤ 0.05) در منطقه رد قرار دارد و نتیجه می‌گیریم به احتمال 95/0 فرضیه صفر رد می‌شود. این بدان معناست که به احتمال 95/0 ضریب رگرسیون لجستیک متغیر مستقل X_j در جمعیت مبنای نمونه‌گیری صفر نیست.

به عنوان مثال سطح معناداری آزمون والد ضریب b متغیر جنس (X1) مثال 2 در جدول فوق (ستون ششم) معادل 006/0 است که چون کمتر از 05/0 است نتیجه می‌گیریم به احتمال 95/0 فرضیه صفر رد می‌شود و ضریب متغیر مستقل جنس (X1) در جمعیت کل معادل صفر نیست. به عبارت دیگر به احتمال 95/0 مقدار ضریب رگرسیون متغیر مستقل جنس (X1) به جمعیت تعمیم پذیر است.

اما در جایی که مقدار ضریب رگرسیون بزرگ باشد خطای استاندارد بسیار بزرگ و لاجرم آماره والد بسیار کوچک می‌شود و دیگر نمی‌توان برای آزمون فرضیه صفر بدان اتکا کرد. در این صورت باید مدل با آن متغیر را با مدلی بدون آن مقایسه کرد. اگر تفاوت منهای دو لگاریتم لاکلیهود (-2LL) دو مدل معنادار بود فرضیه صفر رد می‌شود.

هرگاه سطح معناداری ضریب رگرسیون لجستیک یک یا چند متغیر مستقل مفروض محقق بیشتر از 05/0 شود مبین آن است که فرضیات محقق درباره موثر بودن همه متغیرهای مستقل مفروض بر متغیر وابسته تایید نمی‌شود. به عبارت دیگر در این حالت مدل نظری مفروض محقق که همان مجموعه متغیرهای مستقلی است که محقق عوامل موثر در متغیر وابسته فرض کرده است رد می‌شود.

رگرسیون لجستیک کاربرد های متنوعی دارد. در این مقاله به صورت جامع سعی کردیم توضیحات را ارائه دهیم.اما قطعا ممکن است که در میان راه به مشکلاتی برخورد کنید، شما با امکانی که در سایت آمار پیشرو ایجاد شده می توانید مشکلات و سوالات خود را با متخصصین مجرب این حوزه در میان بگذارید. با تکمیل فرم در بخش مشاوره آماری رایگان می توانید از این خدمات استفاده کنید.

روش‌های رگرسیون لجستیک، فرمان بلوک‌بندی متغیرهای مستقل و کنترل اثر متغیرهای مستقل مباحثی هستند که در آینده عنوان خواهیم کرد.شما می توانید با دنبال کردن صفحه اینستاگرام آمار پیشرو جدید ترین مطالب را در آن ببینید.

به منظور انجام پروژه نیز شرکت آمار پیشرو آماده است تا در سریعترین زمان ممکن و با کیفیت بالا این پروژه را به پایان برساند. برای سپردن پروژه به این شرکت آماری در قسمت ثبت سفارش فرم آماده شده را تکمیل فرمایید.