[section label=”Media Top” bg_color=”rgb(193, 193, 193)” bg_overlay=”rgba(255, 255, 255, 0.85)” padding=”0px”]

[row style=”large” h_align=”center”]

[col]

[ux_image id=”1924″ height=”56.25%”]

[/col]
[col span=”7″ span__sm=”12″ align=”center”]

تحلیل آماری پایان نامه با استفاده از مدلسازی معادلات ساختاری

[/col]

[/row]

[/section]

[row]

[col span__sm=”12″]

مدلسازی معادلات ساختاری یکی از پرکاربردترین روش‌های تحلیل آماری در پژوهش‌ها است. در مدلسازی معادلات ساختاری روابط بین متغیرها به طور همزمان بررسی می‌شود. به این معنی که همزمان تاثیر متغیرهای مستقل پژوهش بر متغیر وابسته مورد سنجش قرار می‌گیرد. به زبان ساده‌تر اگر بخواهیم تاثیر ویژگی‌های شخصیتی مدیران که شامل برون گرایی، داشتن روحیه توافق، وجدان کاری، ثبات عاطفی و تجربه اندوزی می‌شود را بر بهره وری عملکرد کارکنان بسنجیم از مدلسازی معادلات ساختاری استفاده می‌کنیم.
شرکت آمارپیشرو با حضور کارشناسان خبره و متخصص مسلط به نرم افزارهای LISREL, AMOS, Smart PLS پروژه های تحقیقاتی شما را با استفاده از روش مدل سازی معادلات ساختاری با بهترین کیفیت و بالاترین سرعت انجام می‌دهد.
مدلسازی معادلات ساختاری تحلیل چندمتغیری از خانواده رگرسیون چند متغیری است و کاربرد اصلی آن در موضوعات چند متغیره‌ای است که نمی‌توان آن را به صورت دو متغیره انجام داد. به زبان ساده‌تر تاثیر همزمان متغیرهای مستقل بر متغیر وابسته را می‌خواهیم مورد بررسی قرار دهیم و نمی‌خواهیم هر بار یک متغیر مستقل در مقابل متغیر وابسته مورد سنجش قرار گیرد.

معرفی نرم افزارهای مدل سازی معادلات ساختاری

مدلسازی معادلات ساختاری به بررسی مجموعه ای از روابط وابستگی به طور همزمان می پردازد. استفاده از این روش، به ویژه زمانی مفید است که یک متغیر وابسته در روابط وابستگی بعدی تبدیل به یک متغیر مستقل می شود. این مجموعه روابط، اساس مدل یابی معادلات ساختاری را تشکیل می دهد.
LISREL, AMOS, EQS, Smart PLS چهار نرم افزار پرکاربرد مدلسازی معادلات ساختاری هستند که نرم افزارهای LISREL, AMOS, EQS متعلق به نسل کواریانس محورها (نسل اول معادلات ساختاری) هستند. نرم افزار Smart PLS متعلق به نسل مولفه محورها (نسل دوم معادلات ساختاری) می‌باشد.

نسل اول مدل سازی معادلات ساختاری (Covariance-based SEM Techniques)

این روش ها که به روش های کواریانس محور معروف هستند، توسط جورسگوک (1969) معرفی شدند. هدف اصلی این روش ها تأیید مدل است که برای این کار به نمونه هایی با حجم بالا نیاز دارند. در این روش به تخمین ضرایب مسیرها و بارهای عاملی با استفاده از به حداقل رساندن تفاوت بین ماتریس های واریانس-کواریانس مشاهده شده و پیش بینی شده می پردازند.
ماتریس واریانس-کواریانس مشاهده شده توسط واریانس و کواریانس محاسبه شده بین متغیرهای مکنون به دست می  آید. پرکاربردترین رویکرد محاسبه ضرایب در روش های نسل اول، رویکرد تخمین حداکثر احتمال است که نیاز به داده  های مربوط به متغیرهای مشاهده شده (سوال ها) دارد که این متغیرها حتما باید از توزیع نرمال پیروی کرده باشند.

نسل دوم مدل سازی معادلات ساختاری(Component-based SEM Techniques)

روش های مولفه محور که بعدا به روش حداقل مربعات جزئی (Partial Least Squares) تغییر نام دادند، توسط ولد (1974) ابداع شد. این روش از دو مرحله تشکیل شده است: 1) سنجش مدل های اندازه گیری با معیارهای مربوط به پایایی و روایی . 2) سنجش بخش ساختاری با استفاده از ضرایب t.
طی سالهای اخیر استفاده از روش PLS و نرم افزارهای مربوط به اون نسبت به روش های نسل اول و نرم افزارهای نسل اول مثل لیزرل، آموس و ای کیو اس، بیشتر شده و این به خاطر مزیت هایی است که روش PLS نسبت به روش نسل اول دارد. این رویکرد به جای باز تولید ماتریس کوواریانس تجربی، بر بیشینه سازی واریانس متغیرهای وابسته که توسط متغیرهای مستقل پیش بینی نی شوند تمرکز دارد.
این رویکرد همانند رویکرد لیزرل، از بخش ساختاری که نمایانگر روابط بین متغیرهای پنهان، و بخش اندازه گیری که نشانگر روابط متغیرهای پنهان با نشانگرهایشان است، تشکیل شده است. در رویکرد (PLS) بخش ساختاری، ندل درونی (Inner model) و بخش اندازه گیری مدل بیرونی (Outer model) نام دارد. اما رویکرد (PLS) علاوه بر این دو بخش دارای بخش سومی نیز می باشد، که نسبت های وزنی(Weight relations) نام دارد.
این بخش جهت برآورد مقادیر موردها(Case value) برای متغیرهای پنهان مورد استفاده قرار می گیرد (نمرات افراد در متغیرهای مکنون). برخلاف رویکرد مبتنی بر کوواریانس که ابتدا پارامترهای مدل برآورده شده و سپس مقادیر موردها از طریق برگشت دادن آنها به مجموعه تمام نشانگرها، برآورد می شود(مانند مقادیر برآورد شده برای هر متغیر پنهان در هر مجموعه از داده ها)، در رویکرد (PLS) ابتدا مقادیر موردها محاسبه می شود.

[ux_banner height=”100%” bg=”1821″ bg_size=”original” bg_overlay=”rgba(0, 0, 0, 0.7)” bg_pos=”76% 42%”]

[text_box width=”94″ scale=”106″ position_x=”50″ position_y=”85″]

خدمات آمار پیشرو به چه کسانی ارائه می گردد؟

[divider align=”center” margin=”0.3em”]

خدمات متنوع شرکت آمارپیشرو در خصوص نرم افزارهای Amos, Lisrel, Smart PLS به دانشجویان، محققان و اساتید در داخل و خارج از کشور و همچنین مسئولین و مدیران دستگاه‌های دولتی و شرکت‌های خصوصی ارئه می گردد

[divider align=”center” margin=”0.3em”]

خدمات آمار پیشرو در خصوص نرم افزارهای Amos, Lisrel, Smart PLS

[gap]

[row_inner style=”collapse” col_style=”dashed” width=”full-width”]

[col_inner span=”4″]

[featured_box img=”1690″ pos=”center” font_size=”small”]

آموزش به صورت حضوری یا مجازی (خصوصی و گروهی ) روش‌های معادلات ساختاری

[/featured_box]

[/col_inner]
[col_inner span=”4″]

[featured_box img=”1930″ pos=”center” font_size=”small”]

مشاوره تلفنی مرتبط با نصب و خروجی نرم افزارها

[/featured_box]

[/col_inner]
[col_inner span=”4″]

[featured_box img=”1931″ pos=”center” font_size=”small”]

انجام تحلیل عاملی تاییدی، برازش مدل و تحلیل مسیر

[/featured_box]

[/col_inner]

[/row_inner]

[/text_box]

[/ux_banner]
[gap]

[/col]

[/row]

با نرم افزارهای معادلات ساختاری چه کارهایی می‌توان انجام داد؟

تحلیل عاملی تاییدی

در مدل‌هاي عاملي فرض بر اين است که نمرات هر مورد مطالعه در يک متغير، در واقع منعکس کننده وضعيت آن مورد در يک عامل زيربنايي‌تر است که به دليل پنهان بودنش امکان اندازه‌گيري مستقيم آن وجود ندارد. به زبان ساده‌تر در تحلیل عاملی تاییدی به دنبال آن هستیم که آیا مدلی با تعداد عامل‌های درنظر گرفته شده بر اساس تئوری و مبانی نظری با مدل مشاهده شده و بارهای عاملی به‌دست آمده انطباق دارد یا خیر؟
مدل‌هاي عاملي تاییدی (مرتبه اول و يا مرتبه بالاتر) مي‌توانند تک عاملي، ‌دوعاملي، ‌سه عاملي و يا با تعداد عامل‌هاي بيشتر باشند. تعداد عامل‌ها در يک مدل عاملي در واقع به تعريف عملياتي پژوهشگر از مفاهيم مورد نظرش در پژوهش مربوط مي‌شود.

تحلیل عاملی مرتبه اول

در تحلیل عاملی تاییدی مرتبه اول (First order confirmatory factor analysis) رابطه بین عامل یا عامل‌ها (متغیرهای پنهان) با گویه‌ها (متغیرهای مشاهده‌پذیر) مورد سنجش قرار می‌گیرد. در تحلیل عاملی مرتبه اول رابطه بین متغیرهای پنهان مورد بررسی قرار نمی‌گیرد. در واقع تنها يک لايه از متغير يا متغيرهاي پنهان در مدل وجود دارد. در اين مدل متغير مورد نظر به عنوان يک عامل پنهان، خود بعدي از ابعاد يک عامل پنهان در مرتبه بالاتر نيست. جهت پيکان‌ها از سمت متغير در نقش يک عامل پنهان به سمت ابعاد چندگانه به اين دليل با اهميت روش شناختي صورت مي‌گيرد که بالا يا پايين بودن نمره افراد در ابعاد چندگانه مورد نظر در واقع منعکس کننده بالا يا پايين بودن متغير پنهان مورد نظر براي آن گروه از افراد است. به عبارت ديگر مي‌توان گفت به اين دليل که افراد اگر در متغير پنهان داراي نمره بالايي باشند در ابعاد نيز نمره بالايي مي‌گيرند (و بالعکس).

تحلیل عاملی مرتبه دوم

در تحلیل عاملی تاییدی مرتبه دوم (Second order confirmatory factor analysis) یک سازه بزرگ خود از چند متغیر پنهان تشکیل شده است. مدل عاملي مرتبه دوم را به عنوان نوعي از مدل‌هاي عاملي تعريف مي‌کنيم که در آن عامل‌هاي پنهاني که با استفاده از متغيرهاي مشاهده شده اندازه‌گيري مي‌شوند خود تحت تاثير يک متغير زيربنايي‌تر و به عبارتي متغير پنهان، اما در يک سطح بالاتر قرار دارند. چنين موقعيتي باعث مي‌شود تا نوع متغيرهاي حاضر در يک مدل عاملي مرتبه دوم و همچنين پارامترهاي آزاد آن در مقايسه با مدل عاملي مرتبه اول تفاوت قابل توجهي داشته باشد. در تحلیل عاملی تاییدی مرتبه دوم علاوه بر بررسی رابطه متغیرهای مشاهده‌پذیر با متغیرهای پنهان، رابطه متغیرهای پنهان با سازه اصلی خود نیز بررسی می‌شود. مدل‌هاي عاملي مرتبه دوم با وجود کاربردي بودن کمتر مورد استفاده پژوهشگران قرار مي‌گيرند که يکي از دلایل مهم آن مشکلاتي است که اين نوع از مدل‌ها در مرحله تشخیص مدل با آن مواجه مي‌شوند. در مرحله تشخيص، ‌امکان برآورد پارامترها با توجه به اطلاعات موجود در ماتريس کوواريانس مشاهده شده بررسي مي‌شود. اگر تنها يکي از پارامترها امکان برآورد نداشته باشند آن پارامتر را نامشخص مي‌نامند. چنانچه در يک مدل تنها يک پارامتر نامشخص وجود داشته باشد آن مدل نامشخص بوده و نرم افزارهاي مدل‌سازي امکان برآورد ساير پارامترهايي که در مدل مشخص هستند را نيز ندارند. در چنين وضعيتي معمولا پژوهشگر مايل است برخي از پارامترهاي آزاد در مدل را به عنوان پارامتر ثابت فرض کند تا مدل مشخص شده و امکان برآورد پارامترها فراهم شود.

برازش مدل‌هاي اندازه‌گيري(Measurable Models Goodness Fit )

يکي از روش‌هاي جامع و مفيد که نويسندگان اغلب براي انتخاب نوع مدل‌هاي اندازه‌گيري در مدل مفهومي پژوهش خود از آن استفاده مي‌کنند روش چهار قاعده اي جارويس و همکاران است. اين چهار قاعده براي مدل‌هاي سازنده و انعکاسي به شرح زير است:
جهت رابطه علت و معلولي بين سازه و شاخص:
جهت رابطه علت و معلولي در مدل سازنده از سوال پرسشنامه به متغير تحقيق ترسيم مي‌گردد در حالي که در مدل انعکاسي اين جهت از سمت متغير به سمت سوال پرسشنامه مي‌باشد. در اين تحقيق مدل انعکاسي مي‌باشد.
همبستگي متقابل بين سوال‌هاي هر متغير:
در مدل سازنده همبستگي متقابل بين سوالات حتمي نيست در حالي که در مدل انعکاسي سوالات حتما همبستگي زيادي با هم دارند.
تغيير همزمان سوالات با هم:
در مدل سازنده تغيير در يک سوال، لزوما تغيير در سوالات ديگر را به همراه ندارد در حالي که در مدل انعکاسي انتظار مي‌رود که با تغيير در يک سوال، آثار تغيير در تمامي سوالات ديگر نيز نمايان شود.
پيش‌بين‌ها و پيامدهاي سوالات يک متغير:
در مدل سازنده لزوما سوالات پيش‌بين‌ها و پيامدهاي يکساني ندارند در حالي که در مورد مدل انعکاسي سوالات حتما پيش‌بين‌ها و پيامدهاي يکساني دارند.

برازش مدل ساختاري Structure Model Goodness Fit

بعد از بررسي برازش مدل‌هاي اندازه‌گيري نوبت به برازش مدل ساختاري پژوهش مي‌رسد. همانگونه که قبلا اشاره شد، بخش مدل ساختاري بر خلاف مدل‌هاي اندازه‌گيري، به سوالات (متغيرهاي آشکار) کاري ندارد و تنها متغيرهاي پنهان همراه با روابط ميان آنها بررسي مي‌گردد.

برازش مدل کليTotal Model Goodness Fit

مدل کلي شامل هر دو بخش مدل اندازه گيري و ساختاري مي شود و با تاييد برازش آن، بررسي برازش در يک مدل کامل مي شود.
معيار GOF) Goodness Of Fit):
معيار GOF مربوط به بخش کلي مدل هاي معادلات ساختاري است. بدين معني که توسط اين معيار محقق مي تواند پس از بررسي برازش بخش اندازه گيري و بخش ساختاري مدل کلي پژوهش خود، برازش بخش کلي را نيز کنترل نمايد. معيار GOF توسط تننهاوس و همکاران (Tenenhaus et al) در سال 2004 ابداع گرديد و فرمول آن در زير آمده است.
Communality (مقادير اشتراکي) = اين مقدار از ميانگين مجذور بارهاي عاملي هر متغير به دست مي آيد.

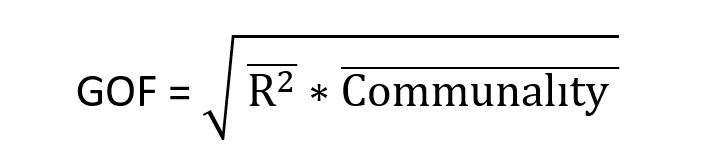
Communality (مقادير اشتراکي) = اين مقدار از ميانگين مجذور بارهاي عاملي هر متغير به دست مي آيد.

Communality √= از ميانگين مقادير اشتراکي هر متغير درون زاي مدل به دست مي آيد.

R² =ميانگين مقادير R Square متغيرهاي درون زاي مدل است.

تحلیل مسیر

تحلیل مسیر یا path analysis جهت و شدت رابطه بین متغیرها را نشان می‌دهد. به زبان ساده تر در تحلیل مسیر به بیان روابط بین متغیرهای تحقیق می‌پردازیم. آن مقادیری که جهت و میزان تاثیر بین متغیرها را نشان می‌دهد ضریب مسیر نام دارد.

[section padding__sm=”0px”]

[row]

[col span__sm=”12″]

[gap height=”25px”]

[ux_banner height=”500px” bg=”1936″ bg_overlay=”rgba(63, 89, 94, 0.26)” bg_pos=”51% 61%”]

[text_box width=”35″ width__sm=”75″ position_x=”5″ position_x__sm=”10″ position_y=”90″ text_align=”left”]

در حال از دست دادن زمان هستید!!!

کار خودتان را راحت کنید

همین الان می توانید با کارشناسان ما به صورت کاملا رایگان مشاوره کنید و یا سفارش خود را ثبت و ادامه کار را به تیم توانمند آمار پیشرو بسپارید و از این همکاری لذت ببرید

[row_inner style=”collapse”]

[col_inner span=”4″ span__sm=”3″ padding=”0px 0px 0px 0px” margin=”0px 0px 0px 0px” align=”left”]

[button text=”مشاوره رایگان” color=”white” style=”underline” link=”https://amarpishro.com/free-consultation-with-amar-pishro/”]

[/col_inner]
[col_inner span=”4″ span__sm=”2″ padding=”0px 10px 0px 0px” align=”center”]

[button text=”ثبت سفارش” color=”white” style=”underline” link=”https://amarpishro.com/statistic-service-analysis-order/”]

[/col_inner]

[/row_inner]

[/text_box]

[/ux_banner]

[/col]

[/row]

[/section]