آمار توصیفی چیست؟ چه راه های برای خلاصه کردن داده ها وجود دارد؟

آمار توصیفی در SPSS کاربرد های فراوانی دارد. این کاربرد ها فقط مخصوص رشته های آماری نیست. بلکه تمام رشته ها درگیر خواهد کرد.

آمار توصیفی آن دسته از علم آمار است که با دسته‌بندی، طبقه‌بندی، خلاصه‌سازی، نمایش ترسیمی و تلخیص داده‌ها سروکار دارد. در آمار توصیفی برای خلاصه‌سازی داده‌ها از جداول و نمودارها و محاسبه مقادیری مانند میانگین، میانه، نما، واریانس، انحراف معیار و … استفاده می‌شود.

هدف اصلی آمار توصیفی، تهیه اطلاعات به صورت یک فرم مناسب، قابل استفاده و قابل فهم است. واضح است که از داده‌های خام به تنهایی نمی‌توان اطلاعاتی کسب کرد و باید تا آنجا که می‌توان آن‌ها را به وسیله نمودار و یا چند عدد که شاخص و معرف آن است، خلاصه نمود. برای خلاصه کردن داده‌ها روش‌های زیر متداول است:

1. جداول
2. نمودارها
3. معیارهای عددی

آمار توصیفی یکی از بخش های اصلی تحلیل آماری است که در بیشتر تحقیقات و پژوهش های علمی مورد توجه قرار می گیرد.

خلاصه آمار توصیفی در جداول

جدول فراوانی

برای داده‌ها از نوع کیفی و یا کمی گسسته به تعداد زیاد، از این جداول استفاده می‌شود به عنوان مثال برای دسته بندی افراد با میزان تحصیلات متفاوت از جدول فراوانی استفاده می‌شود.

جدول طبقه بندی

اگر تعداد داده‌های پیوسته و یا گسسته بسیار زیاد باشد، استفاده از جدول فراوانی مناسب نیست در اینجا فاصله‌ای را که داده‌ها به آن تعلق دارند به تعدادی زیرفاصله تقسیم می‌کنیم مثلا اگر [a,b] فاصله‌ای باشد که داده‌ها به آن تعلق دارند به طوری‌که a مقدار مینیمم و b مقدار ماکزیمم است. با استفاده از فرمول زیر به K رده با طول برابر تقسیم می شود.

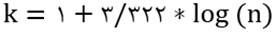
در این قسمت جدول مربوط به هر قسمت را رسم می کنیم.

جدول توافقی

این جداول رابطه بین دو یا چند متغیر رده‌ای را نشان می‌دهد و میزان همبستگی آنها را بررسی می‌کند. اینگونه جداول برای متغیرهای اسمی و ترتیبی به کار می‌روند به عنوان مثال یک جدول توافقی ۲*۲ به صورت زیر نمایش داده می‌شود:

مثلا تعداد زنانی که باسواد هستند ۲۵ نفر است و یا تعداد کل باسوادان ۵۹ نفر است و …

خلاصه آمار توصیفی در نمودار

برای نمایش توزیع‌های فراوانی، اغلب از نمودار استفاده می‌شود. نمودارها کمک می‌کنند که تصویر توزیع به روشنی دیده شود. نمودارها برای استفاده‌های عملی و کاربردی مفیدند. به طور کلی نمودارها ساده‌ترین و سریع‌ترین راه انتقال اطلاعات هستند. روش نمایش داده‌ها با توجه به نوع مقیاس آنها انتخاب می‌شود. اگر مقیاس داده‌ها از نوع فاصله‌ای و نسبی باشد، از مقیاس کمی و اگر مقیاس داده‌ها از نوع اسمی یا رتبه‌ای باشد از نمودارهای وصفی استفاده می‌شود.

رسم نمودار آمار توصیفی در SPSS

نرم‌افزار SPSS قابلیت ارائه نمودارهای نسبتا زیادی را دارد. در نرم افزار SPSS  جهت ارائه نمودارها از منوی  Graphs استفاده می‌شود. همچنین می‌توان از گزینه‌هایی که در دستورهای دیگر است جهت ارائه نمودارها استفاده کرد مانند گزینه chart در دستور frequencies. همچنین همه نمودارها در این نرم‌افزار را می‌توان ویرایش کرد.

نرم افزار SPSS چیست؟ 

نمودارهای کمی

نمودار بافت نگار یا هیستوگرام

خلاصه شده مجموعه بزرگ داده‌ها به صورت توزیع فراوانی را می‌توان به کمک نمودار هیستوگرام نمایش داد. این نمودار نمایش مناسبی از الگوی توزیع است. برای رسم این نمودار از فراوانی مطلق یا فراوانی نسبی و حدود واقعی طبقات استفاده می‌شود. این نمودار متشکل از مستطیل‌هایی است که قاعده آنها طول طبقه و ارتفاع‌شان فراوانی نسبی یا مطلق هر طبقه می‌باشد.

رسم نمودار هیستوگرام آمار توصیفی در SPSS

برای رسم این نمودار فراوانی و حدود طبقات بکار برده می‌شود محور افقی با حدود طبقات و محور عمودی با فراوانی مندرج می‌شود. برای کشیدن نمودار گام‌های زیر را طی می‌کنیم:

• منوی زیر را انتخاب تا کادر Histogram باز شود.

Graphs legacy Dialogs Histogram

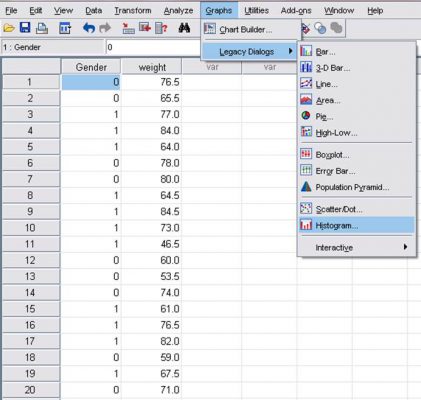
• در این کادر متغیر مورد نظر را انتخاب و به کمک دکمه ( ) به کادر   variable ببرید.
• می‌توانید عنوان نمودار را با کلیک روی دکمه Titles و تایپ نام مورد نظر در جدول مربوطه تعیین کنید.

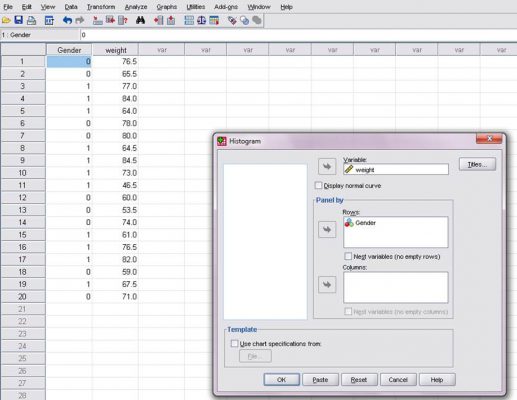
• در قسمت Panel by و کادر Rows متغیر Gender را وارد نمایید تا برای دخترها و پسرها هیستوگرام مجزا رسم شود.
• برای اجرای دستور روی ok کلیک نمایید.
• نمودار هیستوگرام وزن دانش آموزان به تفکیک جنسیت به صورت زیر رسم می‌شود.

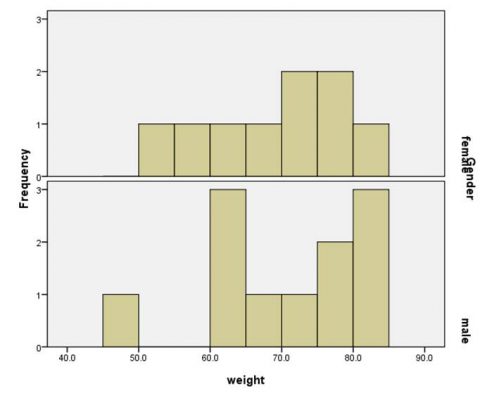
نمودار هیستوگرام فوق نشان می‌دهد آقایان به نسبت خانم‌ها اضافه وزن بیشتری دارند.

نمودارهای چندضلعی یا چندبر

نمودار چند ضلعی نموداریست که نقطه‌ی میانی هر طبقه روی محور افقی و فراوانی نسبی یا مطلق هر یک از نقاط میانی روی محوی عمودی نشان داده می‌شود. متناظر با هر نماینده‌ی طبقه و فراوانی آن یک نقطه در صفحه مشخص می‌شود. به نقاط مزبور دو نقطه‌ی فرضی اضافه می‌کنیم، اولی مرکز طبقه و دیگری نماینده‌ی طبقه‌ی مابعد آخرین طبقه است. به عبارت دیگر، افزودن این دو نقطه‌ی فرضی به این خاطر است که مساحت چندبر با مساحت مستطیل‌ها برابر می‌شود.

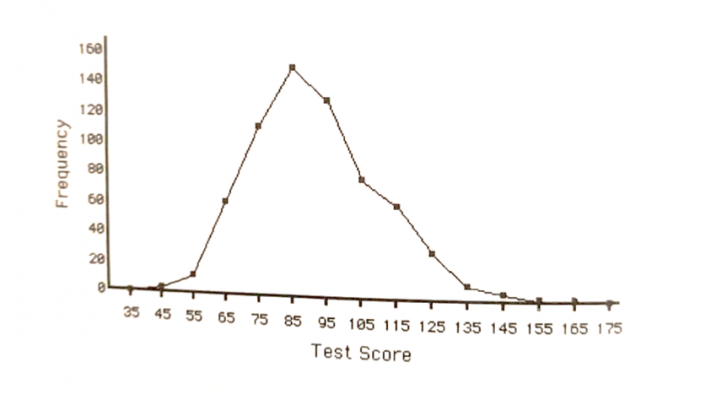
نمودار شاخه و برگ

برای تهیه‌ی نمودار شاخه و برگ، ارقام مشاهدات (حداقل دو رقمی هستند) را به دو قسمت تقسیم می‌کنیم. شاخه، شامل یک یا چند رقم اولیه و برگ، شامل ارقام باقیمانده است. به طور کلی باید شاخه‌های نسبتا کمی در مقایسه با مشاهدات انتخاب کرد (بهتر است این تعداد بین ۵ تا ۲۰ شاخه باشد). هنگامی که مجموعه‌ی شاخه‌ها انتخاب شد، این اعداد در ستون سمت چپ نوشته می‌شوند و در کنار هر شاخه تمام برگ‌های متناظر با مقادیر داده‌ها به ترتیب مشاهده و ثبت می‌شود.

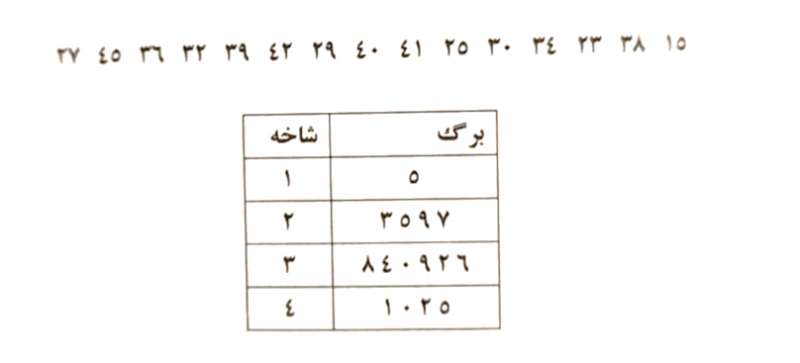
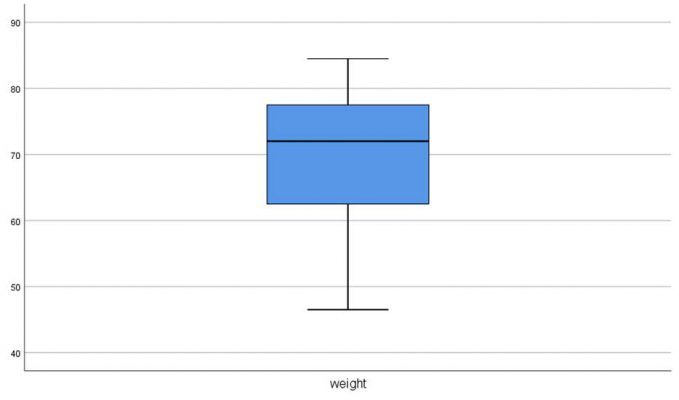
نمودار جعبه‌ای

نمودار جعبه‌ای، یکی از مفیدترین نمودارهای اکتشافی برای مقایسه‌ی دو یا چند جامعه‌ی آماری است. این نمودار نشان‌دهنده‌ی چارک‌ها و حداقل و حداکثر مشاهدات است. در این نمودار، ابتدای جعبه، چارک اول و انتهای آن چارک سوم است (از پایین به بالا) خطی که جعبه را به دو نیم تقسیم می‌کند، میانه‌ی مشاهدات است. از هر طرف جعبه به اندازه نقاط حداقل و  حداکثر، خطی ادامه می‌یابد که به این خط سبیل جعبه گوییم.

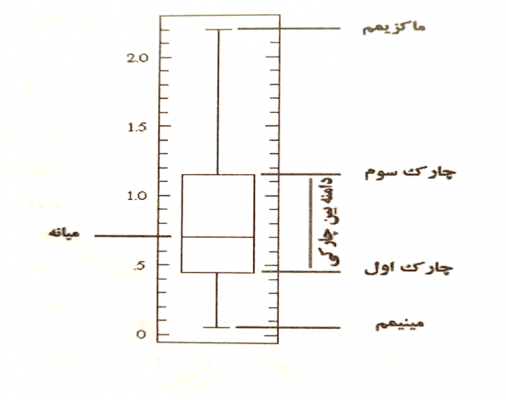
نمودارهای وصفی

این دسته نمودارها برای نمایش هندسی داده‌های کیفی به کار می‌روند. مشاهداتی از نوع خوب، بد، متوسط و یا زن، مرد و .. را می‌توان کیفی دانست. در این حالت، هر مقدار را یک طبقه به شمار می‌آوریم.

نمودار ستونی یا میله‌ای

این نمودار، مناسب‌ترین نمودار برای متغیرهای کیفی است که آن را در یک دستگاه مختصات دکارتی که محور افقی آن نشان‌دهنده‌ی کیفیت مشاهدات و محور عمودی آن نشان‌دهنده‌ی فراوانی مطلق یا نسبی هر گروه است، رسم می‌کنند.

رسم نمودار میله‌ای در SPSS

• منوی زیر را انتخاب کنید تا کادر Bar Chart باز شود.

Graphs legacy Dialogs Bar

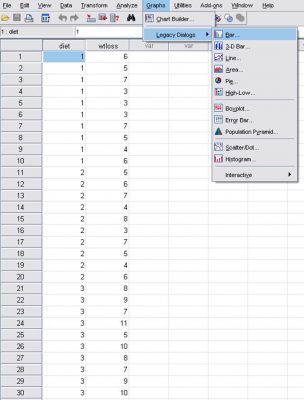
• SPSSدارای قابلیت ارائه نمودارهای ستونی ساده (Simple) ، ستونی خوشه ای (Clustered) و ستونی انباشته (Stacked) می‌باشد. در این‌جا پیش گزیده‌ها را تغییر نمی‌دهیم.
• روی دکمه Define کلیک می‌کنیم تا منوی مربوطه باز شود.
• متغیر weightless را انتخاب و به کادر category Axisببرید.
• در کادر Bar Represent نوع پارامتری که نمودار بر حسب آن رسم می‌شود را مشخص کنید. در این‌جا پیش گزیده N of cases را تغییر ندهید. همچنین در صورت تمایل می‌توانید با کلیک روی دکمه Titles… عنوان نمودار را تعیین کنید.

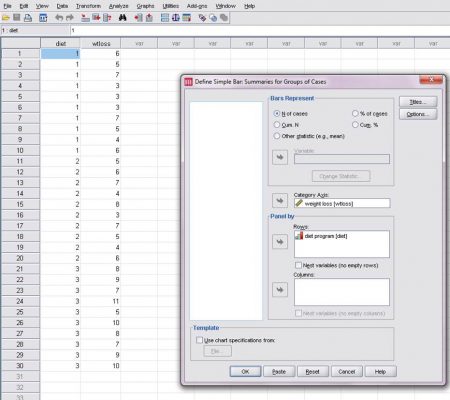
• در قسمت Panel by و کادر Rows متغیر diet program را وارد نمایید تا برای ۳ نوع برنامه رژیم غذایی نمودار مجزا رسم شود.
• برای رسم نمودار روی دکمه ok کلیک کنید.

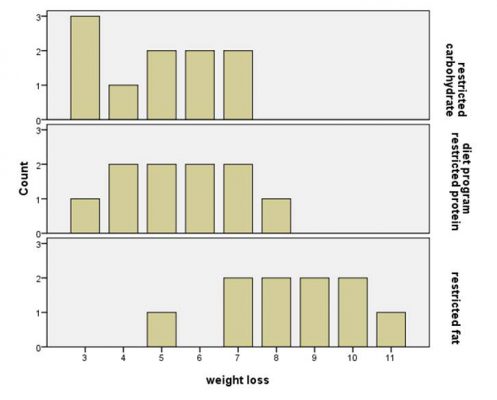
نمودار میله‌ای فوق نشان می‌دهد در بین سه نوع رژیم غذایی در کاهش وزن، رژیم غذایی restricted fat  بیشترین تاثیر در کاهش وزن را داشته است.

نمودار دایره‌ای

این نمودار، ابزار مناسبی برای تجسم مشاهدات کیفی است و معمولا بر اساس درصد رسم می‌شود.

رسم نمودار دایره‌ای در SPSS

منوی زیر را انتخاب کنید تا کادر Pie Charts باز شود.

Graphs legacy Dialogs pie simple

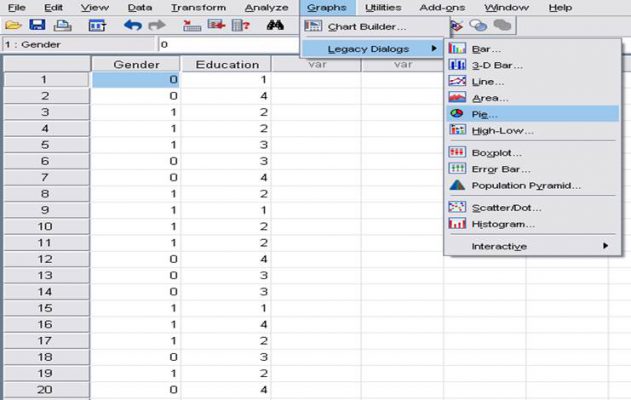
• سپس متغیر gender را انتخاب و به کادر Define slices By ببرید.
• در قسمت Panel by و کادر Rows متغیر Education را وارد نمایید تا برای سطوح متغیر تحصیلات نمودار مجزا رسم شود.

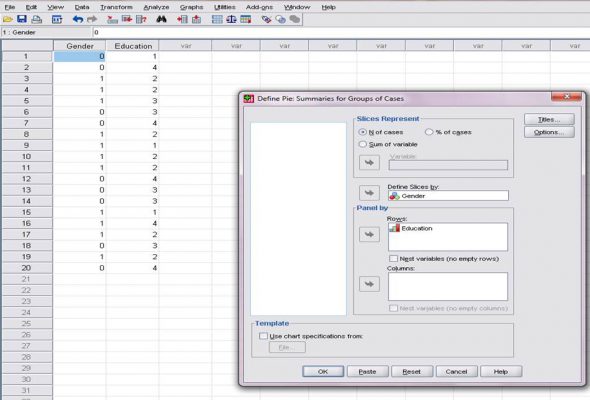
• روی ok کلیک کنید.

نمودار دایره‌ای فوق نشان می‌دهد تعداد افراد بی سواد در آقایان بیشتر از خانم‌هاست و تعداد افرادی که مدرک لیسانس و دیپلم دارند در خانم‌ها بیشتر است.

نمودار پارتو

نمودار پارتو نموداری برای داده‌های وصفی است که در آن فراوانی روی محور عمودی سمت چپ و درصد فراوانی در محور عمودی سمت راست و نوع صفت روی محور افقی آورده می‌شود. این نمودار از یک اقتصاددان ایتالیایی به اسم پارتو اخذ شده است که طبق نظریه‌ی او ۸۰ درصد ثروت جامعه دست ۲۰ درصد افراد آن جامعه است که این اصل، به اصل ۸۰-۲۰ معروف است.

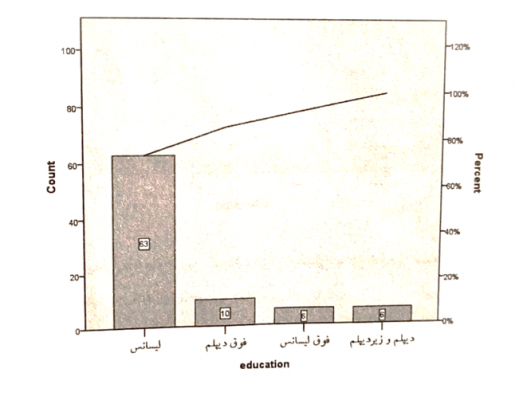
نمودار خطی

در نمودار خطی فراوانی هر طبقه از مشاهدات به کمک یک نقطه نمایش داده می‌شود و این نقاط توسط خطوط مستقیم به نقاط کناری خود وصل می‌شوند. به کمک این نمودار می‌توان به سادگی تغییرات یک متغیر کمی طبقه بندی شده را نمایش داد.

به منظور رسم نمودار خطی مراحل زیر را طی می‌کنیم:

• منوی زیر را انتخاب می‌کنیم.

Graph legacy Dialogs Line

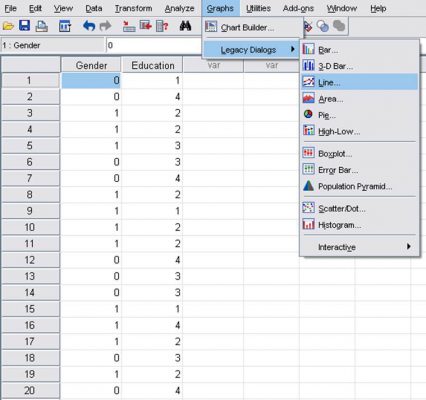
• در کادر Line chart نوع نمودار خطی و روش نمایش داده‌ها را تعیین می‌کنیم. در این‌جا پیش گزیده‌ها را تغییر ندهید و روی دکمه Define کلیک کنید تا کادر مربوطه باز شود.

• متغیرgender را انتخاب و به کادر category Axis  ببرید.
• متغیر education را انتخاب و به کادر Rows  ببرید.

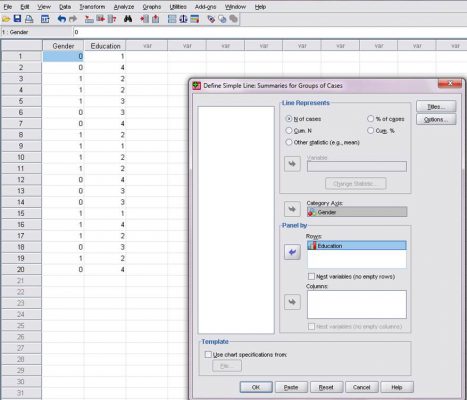
• رای اجرای دستور ok  را انتخاب کنید.

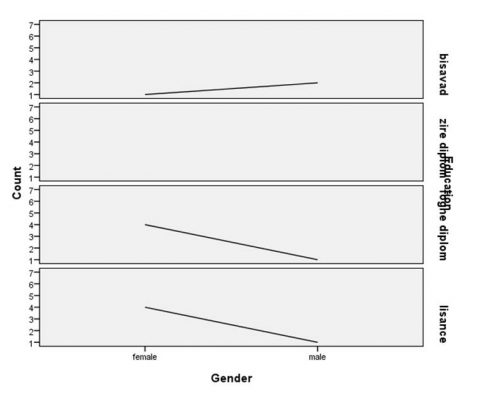
نمودار خطی فوق نشان می‌دهد که در بین کارکنان یک کارخانه بیشترین افراد که مدرک لیسانس و دیپلم دارند خانم‌ها هستند و تعداد افراد بی‌سواد در آقایان بیشتر است و این نشان می‌دهد سطح تحصیلات خانم ها نسبت به آقایان در این کارخانه بیشتر است.

معیارهای عددی در آمار توصیفی

معیارهای عددی، اعدادی هستند جهت توصیف یا تلخیص داده‌ها که به سه صورت زیر وجود دارند:

• معیارهای مرکزی
• معیارهای پراکندگی
• معیارهای شکل (چولگی وکشیدگی)

معیارهای مرکزی آمار توصیفی

نما (Mode)

داده یا داده‌هایی از متغیر است که بیشترین فراوانی را دارد. این شاخص معمولا برای متغیرهای اسمی به کار می‌رود. معمولا از این شاخص نمی‌توان اطلاعات زیادی در مورد داده‌ها کسب کرد و بهتر است که به همراه آن، جدول فراوانی نیز ارائه گردد. واژه‌ی مد، یک واژه فرانسوی است، مثلا وقتی می‌گوییم فلان لباس مد است یعنی تعداد زیادی از افراد آن را می‌پوشند و در آمار هم به همین منظور به کار می‌رود.

برای محاسبه‌ی مد برای داده‌های گسسته یا ترتیبی، ابتدا آنها را به ترتیب صعودی مرتب کرده و عددی که بیشترین فراوانی را دارد، انتخاب می‌کنیم. اگر دو عدد تکرارشان برابر و بیشترین بود و پس از مرتب کردن، این دو عدد در کنار هم قرار گرفتند، ایندو را باهم جمع کرده و میانگین می‌گیریم و میانگینشان را به عنوان مد معرفی می‌‌کنیم. ولی اگر کنار هم قرار نگرفتند، داده‌ها را دو نمایی یا دو مدی می‌نامیم و هر دو را به عنوان مد معرفی می‌کنیم.

میانه (Median)

میانه عددی است که ۵۰ درصد داده‌ها از آن کوچکتر و ۵۰ درصد از آن بزرگتر باشند. برای متغیرهای ترتیبی که می‌توان مقادیر آن‌را از کوچکتر به بزرگتر مرتب کرد، شاخص مرکزی میانه را به کار می‌برند. برای محاسبه‌ی میانه، داده‌ها را به ترتیب صعودی مرتب و داده‌ی متناظر با نفر وسط را پیدا می‌کنیم.

میانگین (Mean)

برای محاسبه‌ی میانگین، داده‌های یک متغیر را جمع و بر تعداد مشاهدات تقسیم می‌کنیم. میانگین داده‌های یک متغیر را که از روی داده‌های نمونه به دست می‌آید، را با نماد  نمایش می‌دهیم.

چندک‌ها

چندک‌ها به سه دسته عمده‌ی چارک‌ها، دهک‌ها و صدک‌ها تقسیم می‌شوند. بطور کل چندک‌ها را بانشان می‌دهیم.

چارک‌ها اعدادی هستند که داده‌ها را به چهار قسمت مساوی تقسیم می‌کنند و با وو نشان داده می‌شوند. عددی است که ۲۵ درصد داده‌ها از آن کوچکترند و عددی است که ۷۵ درصد داده‌ها از آن کوچکترند. همچنین واضح است که همان میانه یا عددی است که ۵۰ درصد داده‌ها از آن کوچکترند. دهک‌ها اعدادی هستند که داده‌ها را به ۱۰ بخش مساوی تقسیم می‌کنند و تقسیری همانند فوق دارند، صدک‌ها هم داده‌ها را به صد بخش مساوی تقسیم می‌کنند.

معیارهای پراکندگی آمار توصیفی

برای متغیرهای اسمی و ترتیبی (که به آن‌ها متغیرهای گسسته نیز گوییم) شاخص‌های پراکندگی، فراوانی‌ها و درصدهای مشاهدات هستند که در جداول فراوانی می‌آیند. برای متغیرهای کمی (که به آن‌ها متغیرهای تصادفی پیوسته می‌گوییم) شاخص‌های پراکندگی به صورت زیر است:

واریانس و انحراف معیار

برای محاسبه واریانس که پرکاربردترین شاخص پراکندگی است، مربع فاصله تمام مقادیر از میانگین را جمع و حاصل را تقسیم بر تعداد مشاهدات منهای ۱ می‌کنیم. به عبارت دیگر، واریانس به معنی میانگین مربع فاصله‌ی مقادیر یک متغیر از میانگین آن متغیر است که فرمول محاسبه آن را بانشان می‌دهیم و به صورت زیر محاسبه می‌شود.

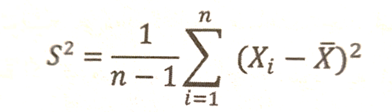
اگر واریانس صفر شود نتیجه می‌گیریم که تمام داده‌ها دارای مقدار مساوی هستند، یعنی هیچگونه پراکندگی اطراف میانگین وجود ندارد، در اینجا توزیع تابع را تباهیده گوییم. برای به دست آوردن شاخص پراکندگی که واحد آن با واحد اندازه‌گیری متغیر اصلی مطابق باشد از واریانس جذر می‌گیریم و انحراف معیار به دست می‌آوریم و با S نشان می‌دهیم.

ضریب تغییرات

ضریب تغییرات، نسبت انحراف معیار به مقدار میانگین را نشان می‌دهد. ضریب تغییرات به واحدی که متغیر مربوط با آن اندازه‌گیری شده است، بستگی ندارد و می‌توان پراکندگی دو متغیر متفاوت را با هم مقایسه نمود. برای مثال می‌توان پراکندگی قیمت ماشین‌های سواری (تومان) را با پراکندگی قد افراد (متر) مقایسه نمود. برای محاسبه‌ی ضریب تغییرات، انحراف معیار را بر قدر مطلق میانگین تقسیم نموده و حاصل را در ۱۰۰ ضرب می‌کنیم، بصورت زیر:

نمرات استاندارد

برای مشخص کردن موقعیت نمره‌ی یک فرد نسبت به نمرات دیگر افراد نمونه، باید نمرات را استاندارد کرد، تا بتوان گفت چقدر نمره‌ی مورد نظر از متوسط نمرات فاصله دارد. برای انجام این کار ابتدا نمره‌ی مشاهده شده را از میانگین کسر و سپس بر انحراف معیار تقسیم می‌کنیم.

نشان‌دهنده‌ی فاصله‌ی یک مشاهده از میانگین یا به مفهوم دیگر بیانگر میزان انحراف از میانگین است. چون می‌خواهیم مقدار این عبارت، مستقل از انحراف معیار شود (یعنی انحراف معیار هیچ تاثیری بر آن نگذارد) آن‌را تقسیم بر انحراف معیار می‌کنیم. نمره استاندارد را با Z نمایش داده و به صورت زیر محاسبه می‌کنیم:

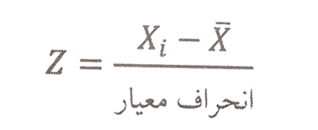
نمره‌ی استاندارد، نشان می‌دهد که یک مشاهده، چند انحراف معیار بیشتر یا کمتر از میانگین می‌باشد. اگر نمره‌ی استاندارد صفر شود، به این معناست که مقدار نمره‌ی مشاهده شده برابر با مقدار میانگین می‌باشد. یا اگر نمره‌ی استاندارد ۲ شود، مقدار مشاهده شده، دو انحراف معیار بالاتر از میانگین است. میانگین نمرات استاندارد همیشه برابر با صفر و انحراف معیار آن ۱ می‌باشد و به صورت زیر نشان می‌دهند:

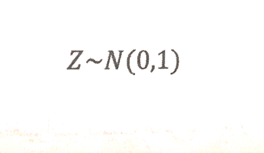
معیارهای شکلی آمار توصیفی

چولگی (Skewness)

میزان عدم تقارن توزیع را اندازه‌گیری و بیان می‌کند، این میزان برای توزیع نرمال صفر است.

کشیدگی (Kurtosis)

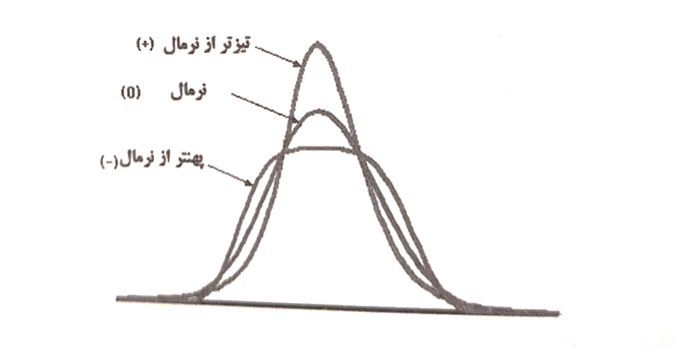
نشان دهنده‌ی قله‌مندی (درجه اوج) یک توزیع احتمالی است، این میزان برای توزیع نرمال ۳ است. برای مقادیر بیشتر از ۳ می‌گوییم توزیع تیزتر از نرمال و برای مقادیر کمتر از ۳ می‌گوییم توزیع پهن‌تر از نرمال است. در نرم افزار مقدار کشیدگی منهای ۳ حساب می‌شود. در این صورت این میزان برای توزیع نرمال صفر می‌باشد. برای مقادیر بیشتر از صفر می‌گوییم توزیع تیزتر از نرمال و برای مقادیر کمتر از صفر می‌گوییم توزیع پهن‌تر از نرمال است.

آمار توصیفی در SPSS

از فرمان Descriptive Statistics  در نرم‌افزار SPSS برای محاسبه آماره‌های توصیفی، تشکیل جدول فراوانی و جداول توافقی و معیارهای عددی استفاده می‌شود. مهم‌ترین فرمان‌های این منو را توضیح می‌دهیم.

فرمان Frequencies

از این فرمان برای تشکیل جداول فراوانی متغیرهای اسمی و رتبه‌ای استفاده می‌شود. همچنین می‌توانید از این جداول برای متغیرهای کمی نیز استفاده کنید. ولی لازم است آن متغیر را مجددا کدگذاری نمایید. برای اجرای این فرمان، از منوی Analyze به ترتیب زیر منوهای Descriptive Statistics و Frequencies را انتخاب می‌کنیم.

فرمان Descriptive

از این فرمان برای محاسبه آماره‌های توصیفی استفاده می‌کنیم. برای این منظور از منوی  Analyze به ترتیب زیر منوهای Descriptive Statistics و Descriptive را انتخاب می‌کنیم.

فرمان Explore…

با فرمان قبلی توانستیم برخی از آماره‌های توصیفی را محاسبه کنیم ولی تعداد آماره‌های توصیفی بسیار بیشتر است. با این فرمان تعداد بیشتری از این آماره‌ها را محاسبه می‌کنیم. این فرمان نسبت به فرمان قبلی انعطاف بیشتری دارد یعنی می‌توان آماره‌های توصیفی را بر حسب متغیر گروه‌بندی کننده نیز به‌دست آورد.

در ادامه فرمان‌های فوق را در SPSS اجرا و خروجی را نمایش داده‌ایم. برای متغیرهای قد و وزن در فایل داده‌های زیر آماره‌های توصیفی به شرح زیر است:

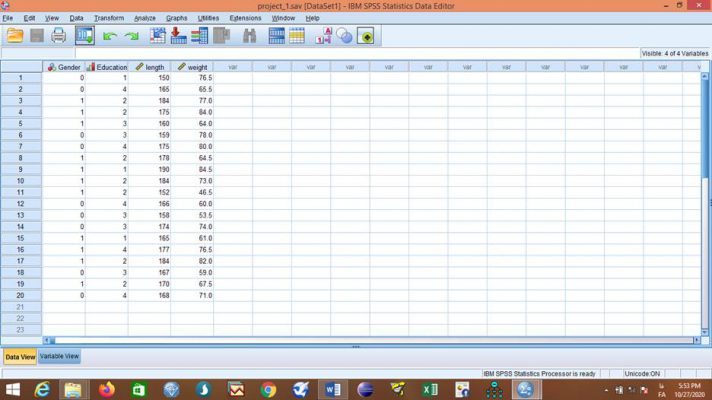
از منوی Analyze به ترتیب زیر منوهای Descriptive Statistics و Explore را انتخاب می‌کنیم.

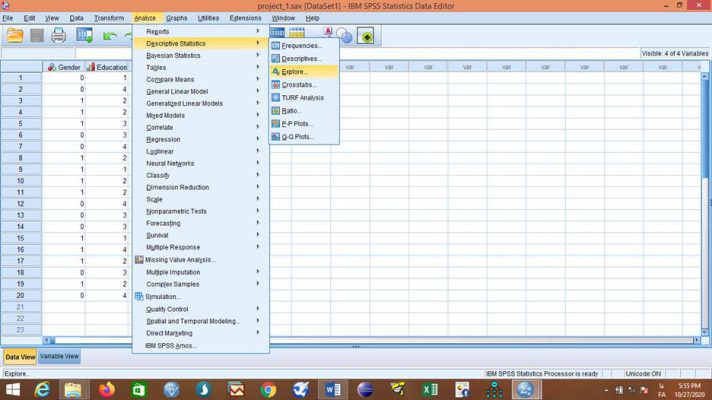
متغیرهای قد و وزن را به باکس Dependent List انتقال داده و در قسمت Display گزینه Both را انتخاب می‌کنیم که آماره‌های توصیفی و نمودارهای مربوطه به صورت همزمان نمایش داده شوند.

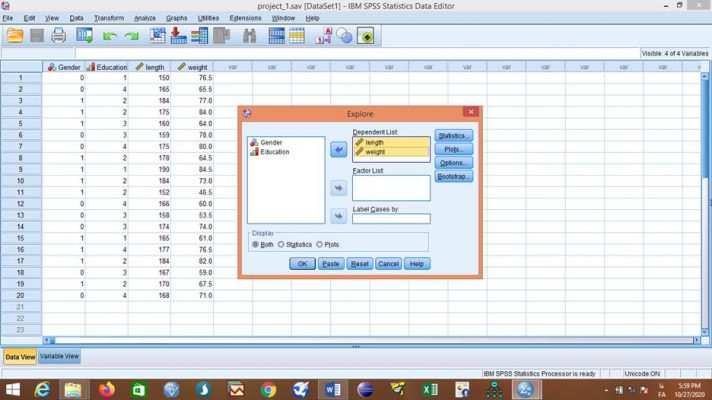
از طریق گزینه Statistics… تیک مربوط به گزارش چندک‌ها و داده‌های پرت را می‌زنیم:

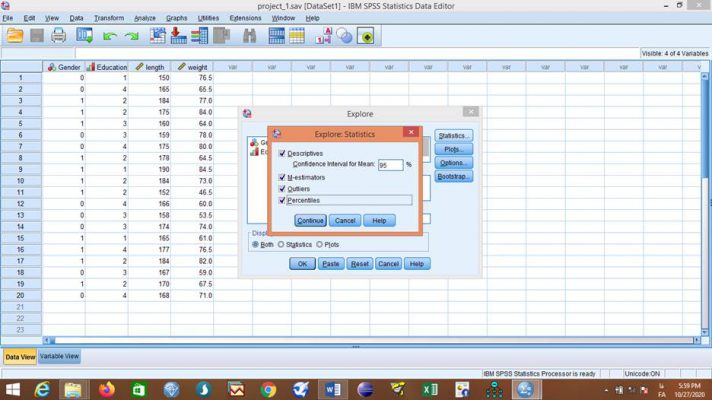
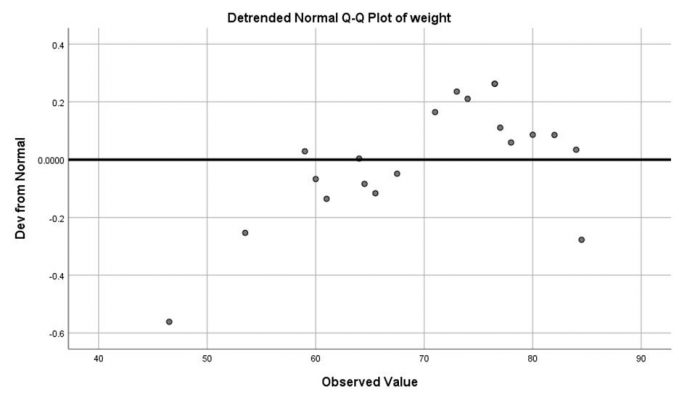
از طریق گزینه Plots… تیک مربوط به رسم نمودارهای جعبه‌ای، ساقه و برگ و هیستوگرام و همچنین انجام آزمون نرمالیتی را می‌زنیم:

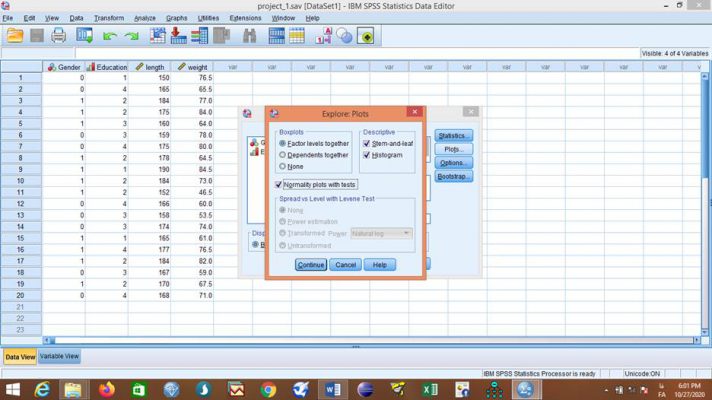
در ادامه روی گزینه OK کلیک کرده و خروجی به صورت زیر نمایش می‌یابد:

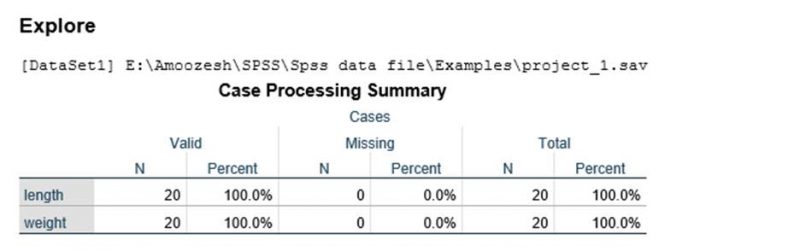
تعداد نمونه‌های مربوط به دو متغیر قد و وزن ۲۰ نمونه بوده و داده گمشده نداشتیم. آماره‌های توصیفی متغیرهای قد و وزن شامل میانگین، میانه، واریانس و … در جدول زیر گزارش شده است:

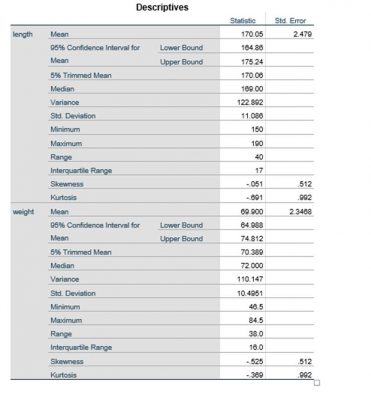
برای هر دو متغیر قد و وزن کوچکترین و بزرگترین مقادیر که می‌توانند جز داده‌های پرت باشند و چندک‌های ۵ تا ۹۵ درصد در جدول زیر آمده است:

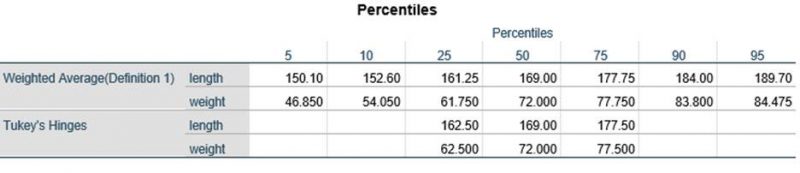
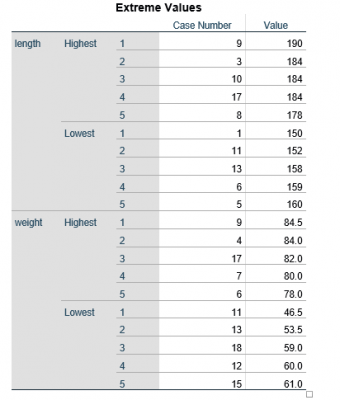
length

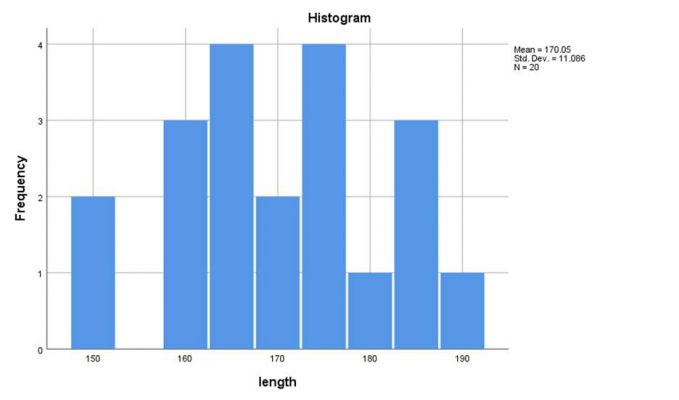
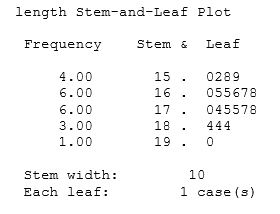
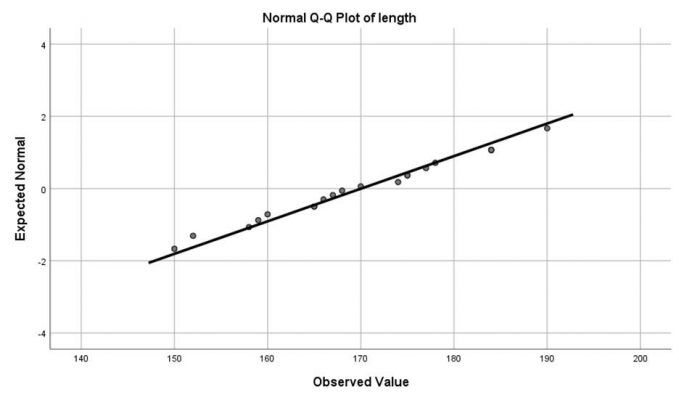
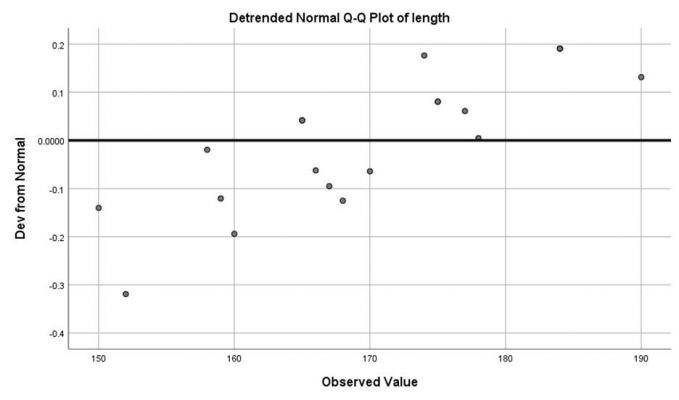
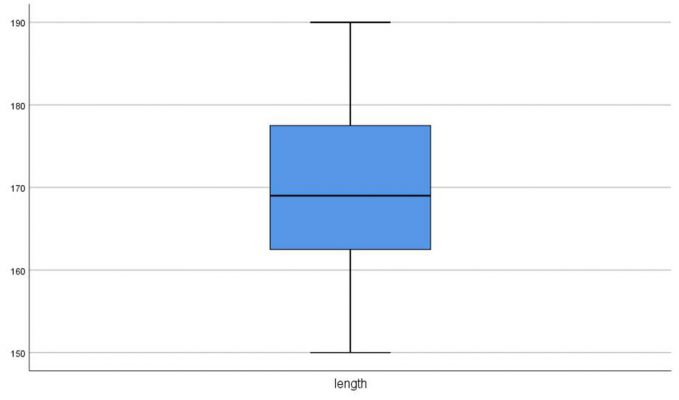
weight

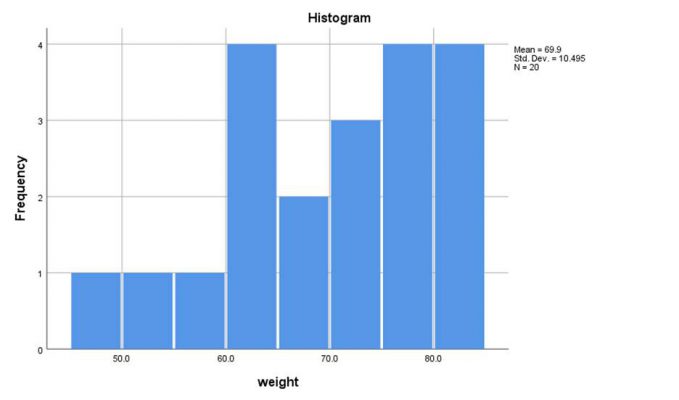
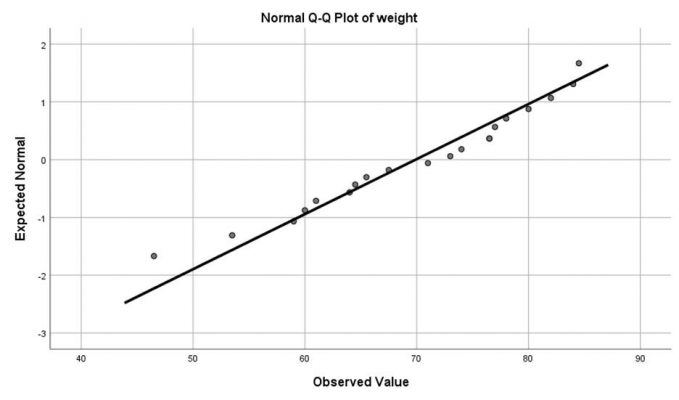
آمار توصیفی یکی از پایه ای ترین مباحث علم آمار است. بسیاری از افراد نسبت به تعریف این آمار و شاخص های آن همت گماردن، اما مساله ای مهمتر فهم این مطالب در کاربرد است. به همین دلیل آمار توصیفی در SPSS از اهمیت بسزایی برخوردار است. با این تفاسیر در این مسیر نیز برخی از پروژه ها دچار مشکل خواهد شد، برای پوشش دادن این دغدغه شما می توانید با متخصصان مجرب و حرفه ای به صورت رایگان مشورت کنید. برای بهره مندی از این مشاوره ها می توانید در قسمت مشاوره آماری رایگان فرم را پر کنید و منتظر تماس متخصصان در اولین فرصت باشید.

اگر علاقه مند به مباحث آماری هستید شما می توانید با دنبال کردن صفحه اینستاگرامی آمار پیشرو از جدید ترین مطالب این حوزه با خبر شوید.

در این مطلب سعی کردیم با مثالی کاربردی آمار توصیفی در SPSS برای شما تشریح کنیم. اما چنانچه در ادامه مسیر نیاز به افراد خبره و متخصص وجود دارد می توانید با ثبت سفارش بر روی سایت و پر کردن فرم پروژه خود را به متخصصان بسپارید.