طی دهه گذشته متوسط کسب و کار به شدت تغییر کرده است. این امر هم شامل تجهیزاتی می شود که بر روی میزها استفاده می شدند و هم شامل نرم افزارهایی که از آنها برای برقراری ارتباط استفاده می کردند. در واقع چیزهای کمی هستند که هنوز هم مثل گذشته باقی مانده اند. این امر در مورد مقدار داده هایی که امروزه در دسترس ما هستند و روش های تحلیل آماری هم صدق می کند.
چطور می توان با داشتن مقدار زیادی داده و توانایی تجزیه و تحلیل مناسب آنها از نقطه الف به نقطه ب رفت؟ همه چیز به استفاده از روش های مناسبی برمی گردد که برای تجزیه و تحلیل استفاده می کنید؛ یعنی نحوه پردازش و نیز چگونگی جمع آوری نمونه هایی از داده ها برای کشف الگوها و روندهای موجود.
برای انجام چنین تحلیلی پنج روش وجود دارند که می توانید از بین آنها روشی را انتخاب کنید؛ میانگین، انحراف معیار، رگرسیون، آزمون فرضیه و تعیین حجم نمونه.

پنج روش برای انجام تجزیه و تحلیل آماری

فرقی نمی کند که دانشمند داده های آماری باشید یا نه، ولی به هر حال نمی توانید منکر شوید که در حال حاضر جهان دچار وسواس نسبت به کلان داده ها شده است. برای همین است که باید بدانید از کجا شروع کنید. در اینجا به بیان و بررسی پنج روش انجام تجزیه و تحلیل آماری می پردازیم که برای رسیدن به نتایج دقیق مبتنی بر داده ها بسیار تاثیرگذار می باشند.

۱. میانگین

اولین روشی که از آن برای انجام تجزیه و تحلیل آماری استفاده می کنند، میانگین است. وقتی که قصد دارید میانگین را حساب کنید، لیستی از اعداد را با هم جمع کرده و سپس عدد به دست آمده را بر تعداد اعدادی که جمع بسته شده اند، تقسیم می کنید.
وقتی از این روش استفاده می شود، اجازه می دهد که یک روند کلی برای مجموعه ای از داده ها و نیز توانایی به دست آوردن نمایی سریع و مختصر از داده ها به وجود آید. کاربران این روش از محاسبه ای سریع و ساده هم بهره منده شده اند.
میانگین آماری برای به دست آوردن نقطه میانی داده های در حال بررسی مطرح می شود. نتیجه نیز میانگین داده های ارائه شده نامیده می شود. در زندگی واقعی، معمولا مردم از میانگین برای انجام تحقیقات، نمرات تحصیلی و ورزش ها استفاده می کنند. فقط به این فکر کنید که ضربات یک بازیکن در بیسبال مورد بحث قرار می گیرند؛ به این میانگین می گویند که از روش های تحلیل آماری است.

چگونه میانگین را به دست آوریم؟

برای پیدا کردن میانگین داده ها، کافی است اعداد را با هم جمع کرده و مجموع آنها را بر تعداد این اعداد تقسیم کنید.
مثلا برای اینکه بتوانید میانگین اعداد ۶، ۱۸، و ۲۴ را به دست آورید، ابتدا باید آنها را هم جمع کنید:
۶ + ۱۸ + ۲۴ = 48
حالا عدد به دست آمده، یعنی ۴۸ را بر تعداد اعداد موجود در لیست، یعنی عدد ۳ تقسیم کنید:
۴۸ / ۳ = 16
میانگین به دست آمده، ۱۶ است.

معایب

اما با همه اینها و با وجود اینکه استفاده از میانگین بسیار هم عالی است، ولی اصلا توصیه نمی کنیم که از آن به عنوان یکی از روش های تحلیل آماری به صورت مستقل استفاده کنید. دلیل آن هم این است که چنین کاری می تواند به صورت بالقوه همه تلاش های پشت پرده محاسبه ها را نابود کند، چون هم به مد (مقداری که اغلب اوقات رخ می دهد) مرتبط است و هم به میان شماره برخی از مجموعه داده ها.
وقتی که با تعداد زیادی از نقاط داده، چه به صورت تعداد زیادی از نقاط دور افتاده (نقاط داده ای که به صورت مشخصی از دیگر نقاط متفاوت هستند) و یا به صورت توزیع نادرستی از داده ها سروکار دارید، میانگین نمی تواند نتیجه خیلی دقیقی را برای تجزیه و تحلیل آماری تصمیمی خاص را ارائه کند.

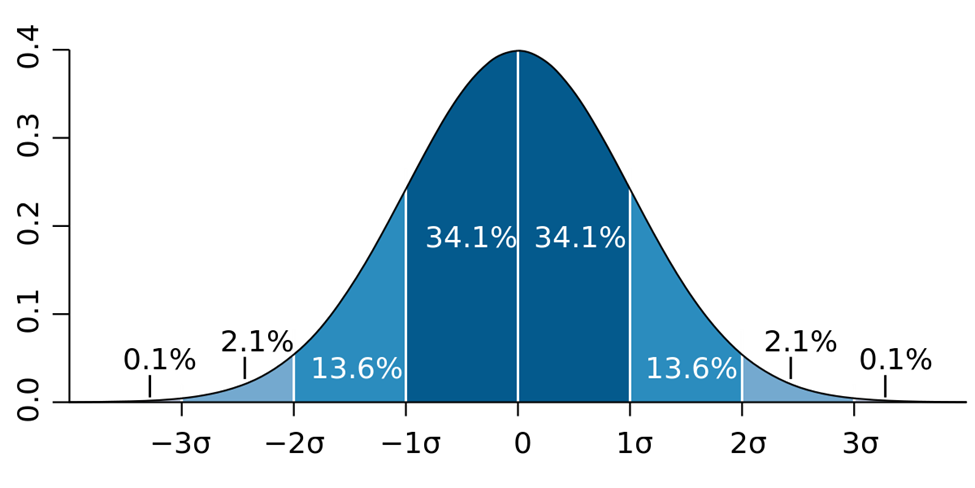
۲. انحراف معیار

انحراف معیار یکی از روش های تحلیل آماری است که پراکندگی داده ها را حول میانگین اندازه گیری می کند. زمانی که با یک انحراف معیار بالا سروکار داشته باشید، به معنای آن است که داده ها به صورت گسترده ای از میانگین فاصله گرفته اند. همچنین انحراف معیار پایین نشان می دهد که اکثر داده ها در راستای میانگین قرار گرفته اند و می توان آنها را مقدار مورد انتظار یک مجموعه نامید.
به صورت عمده زمانی از انحراف معیار استفاده می شود که لازم باشد پراکندگی نقاط داده (چه به صورت خوشه ای و چه غیر از آن) را تعیین کنید. فرض کنید که بازاریابی هستید که اخیرا از مشتریان خود نظرسنجی کرده اید. به محض اینکه نتایج نظرسنجی را به دست آورده اید، می خواهید که قابلیت اطمینان پاسخ ها را اندازه گیری کنید تا ببینید که آیا گروه بزرگ تری از مشتریانتان هم همین پاسخ ها را می دهند یا خیر! در چنین حالتی اگر انحراف معیار پایین باشد، یعنی اینکه تعداد بیشتری از مشتریان همین جواب ها را خواهند داد.

چگونه انحراف معیار را به دست آوریم؟

فرمولی که برای محاسبه انحراف معیار استفاده می شود، این فرمول است:
σ۲ = Σ(x − μ)۲/n
در این فرمول:
σ نماد انحراف معیار است
Σ نشان دهنده مجموعه داده هاست
x مقدار مجموعه داده را نشان می دهد
μ نشان دهنده میانگین داده است
σ۲ واریانس را نشان می دهد
و در نهایت n نشان دهنده تعداد نقاط داده در کل است.
برای پیدا کردن انحراف معیار:

1. میانگین عددهای درون مجموعه داده را پیدا کنید
2. به ازای هر کدام از اعداد درون مجموعه داده، میانگین را کم کرده و جذر حاصل را حساب کنید ( از طریق فرمول (x − μ)۲).
3. میانگین اختلافات مجذور را پیدا کنید.
4. جذر جواب آخر را به دست آورید.
   اگر از همان سه عددی که در مثال میانگین استفاده کردیم، یعنی اعداد ۶، ۱۸، و ۲۴ در اینجا استفاده کنید، انحراف معیار به دست آمده برابر با عدد ۷.۴۸۳۳۱۴۷۷۳۵۴۷۹ خواهد بود.

معایب

درست مثل استفاده از میانگین، اگر از انحراف معیار به صورت تنها روش برای انجام تجزیه و تحلیل آماری استفاده شود، دچار سردرگمی و گیجی خواهید شد.
مثلا اگر داده ای که در حال کار کردن با آن هستید، مقادیر پرت و یا الگوی عجیبی مثل منحنی غیرعادی داشته باشد، انحراف معیار نمی تواند اطلاعات لازم را برای گرفتن تصمیمی آگاهانه به شما ارائه کند.

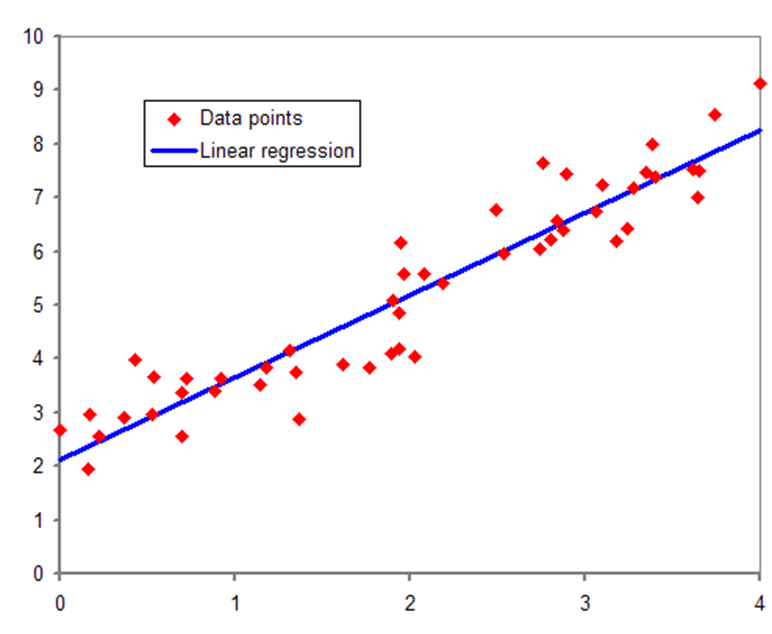
۳. رگرسیون

در بحث مربوط به روش های تحلیل آماری، رگرسیون عبارت است از رابطه بین یک متغیر وابسته (داده هایی که قصد اندازه گیری آنها را دارید) و یک متغیر مستقل (داده هایی که از آنها برای پیش بینی متغیر وابسته استفاده می کنند).
از طرف دیگر، می توان رگرسیون را با استفاده از نحوه تاثیرگذاری متغیری بر متغیر دیگر، و یا تغییرات یک متغیر که باعث ایجاد تغییر در متغیرهای دیگر می شود توضیح داد که همان علت و معلول است. به این معنا که نتیجه به یک یا چند متغیر وابسته است.
خطر مورد استفاده در چارت ها و نمودارهای تحلیل رگرسیون نشان می دهد که روابط بین متغیرها ضعیف یا قوی هستند. به علاوه روندها را در مدت زمانی خاصی نشان می دهد.
این مطالعات در روش های تحلیل آماری برای پیش بینی روندها به کار گرفته می شوند. مثلا این امکان وجود دارد که از رگرسیون استفاده کنید تا بتوانید نحوه فروش یکی از محصولات یا ارائه خدمات خود به مشتریان را پیش بینی کنید. یا اینکه در G2 ما از رگرسیون استفاده می کنیم تا اینکه بتوانیم پیش بینی کنیم که ترافیک اصلی ما طی شش ماه آینده چگونه خواهد بود.

فرمول رگرسیون

فرمول رگرسیون به شرح زیر است:
Y = a + b(x)
که در آن :
a عرض از مبدا است، وقتی که x = 0 نیز مقدار y می باشد
x متغیر وابسته است
Y متغیر مستقل است.
b شیب، یا افزایش در هنگام اجرا را نشان می دهد.

معایب

یکی از معایب استفاده از رگرسیون به عنوان بخشی از تجزیه و تحلیل آماری آن است که رگرسیون نمی تواند خیلی متمایز باشد، یعنی اینکه نقاط دور افتاده بر روی نمودار پراکندگی ( یا نمودار تحلیل آماری رگرسیون) اهمیت دارند، اما دلیل دور افتاده بودن آنها نیز مهم هستند. این امر می تواند به خاطر هرچیزی رخ داده باشد، از یک خطا در تحلیل گرفته تا مقیاس نادرست داده ها.
نقطه داده ای که به عنوان نقطه دور افتاده علامت خورده است، می تواند چیزهای زیادی را نشان دهد، مثلا می تواند پرفروش ترین محصول را نشان دهد. خط رگرسیون شما را فریب می دهد که با نادیده گرفتن این موارد، فقط روندها را در داده ها مشاهده کنید.

۴. آزمون فرضیه

یکی از روش های تحلیل آماری، آزمون فرضیه است که از آن به عنوان نکته کلیدی برای آزمودن دو مجموعه از متغیرهای تصادفی در مجموعه داده ها استفاده می کنند.
این روش فقط درباره آزمایش این است که آیا استدلال یا نتیجه خاصی در مورد مجموعه داده مورد نظر صدق می کند. این روش تحلیل آماری اجازه می دهد که میان داده ها و فرضیه ها و مفروضات مختلف مقایسه انجام بگیرد. همچنین می تواند کمک کند تا درباره اینکه چگونه تصمیمات می توانند بر روی کسب و کار تاثیر بگذارند، پیش بینی های صحیحی انجام شوند.
در آمار، آزمون فرضیه مقداری را تحت یک فرض معین، مشخص می کند. نتیجه آزمون معین می کند که آیا فرض همچنان برقرار است و یا اینکه نقض شده است. به این فرض، فرضیه صفر گفته می شود. هر فرضیه دیگری که مغایر با فرضیه صفر باشد، فرضیه اول نامیده می شود.
با انجام دادن آزمون فرضیه، نکته مهم نتایج آن هستند که اثبات کنند که آماری به صورت تصادفی و شانسی به وجود نیامده است. مثلا ممکن است این فرض را داشته باشید که هرچه زمان توسعه محصولی بیشتر طول بکشد، محصول موفق تری خواهد بود و در نتیجه نسبت به قبل فروش بالاتری خواهد داشت. آزمایش فرضیه می تواند قبل از اینکه ساعات طولانی را برای توسعه محصولی صرف کنید، نشان دهد که آیا واقعا ارتباطی بین آنها هست یا خیر.

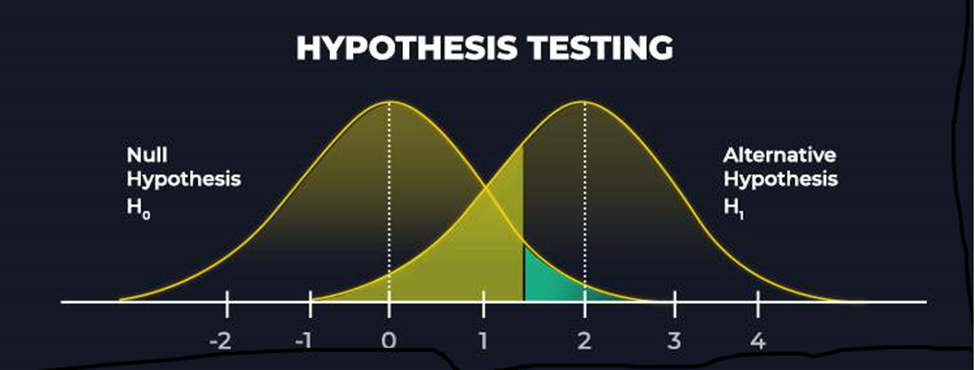
فرمول آزمون فرضیه

نتایج تحلیل آماری بر اساس آزمون فرضیه نیازمند مدعای خاصی است که به آن مقدار p گفته می شود. بگذارید اینگونه فرض کنیم که احتمال درست بودن آنچه به دنبال تعیین آن هستید، ۵۰ درصد است. فرمول آزمون فرضیه به شکل زیر خواهد بود:
H0: P = 0.5
H1: P ≠ ۰.۵

معایب

گاهی اوقات این امکان وجود دارد که آزمون فرضیه به خاطر خطاهای رایج، مثل اثر دارونما دچار ابهام و انحراف شود. این اتفاق زمانی رخ می دهد که تحلیلگران آماری که در حال انجام آزمایش هستند، اشتباهاً انتظار نتیجه خاصی را داشته باشند و سپس بدون توجه به شرایط همان نتیجه را هم به دست آورند.
همین اتفاق هم ممکن است به خاطر اثر هاتورن رخ دهد. این امر زمانی رخ می دهد که شرکت کنندگان به خاطر مطلع بودن از مورد آزمایش بودن، نتایج را به هم بریزند.

۵. تعیین حجم نمونه

یکی از روش های تحلیل آماری برای مجموعه داده هایی که بسیار بزرگ هستند و جمع آوری داده های دقیق برای هر کدام از عناصر مجموعه سخت است، روش تعیین حجم نمونه است. برای انجام صحیح این روش، باید ابتدا اندازه مناسب نمونه را مشخص کرد. اگر حجم نمونه خیلی کوچک باشد، نتایجی که در نهایت به دست می آورید، معتبر نخواهند بود.
برای اینکه بتوان به نتیجه معتبر دست یافت، باید از یکی از روش های نمونه گیری داده ها استفاده کنید. این کار را می توانید با فرستادن نظرسنجی برای مشتریان خود انجام دهید و بعد از روش نمونه گیری تصادفی ساده استفاده کنید تا بتوانید از میان داده های مشتریان برای تجزیه و تحلیل تصادفی انتخاب کنید.
از طرف دیگر، اگر حجم نمونه بیش از حد بزرگ باشد، باعث می شود که هزینه و وقت شما هدر برود. برای اینکه بتوانید اندازه نمونه را تعیین کنید، می توانید جنبه های مختلفی مثل هزینه، زمان، یا حتی راحت بودن جمع آوری داده ها را بررسی کنید.

یافتن حجم نمونه

برخلاف روش های تحلیل آماری که پیش از این گفتیم، فرمولی سخت و سریع برای پیدا کردن حجم نمونه وجود ندارد. با همه این ها می توانید این نکات کلی را برای تعیین حجم نمونه در نظر داشته باشید:
• موقع در نظر گرفتن حجم کمتر، سرشماری انجام دهید.
• از حجم نمونه تحقیقی استفاده کنید که شبیه تحقیق شماست. برای این کار می توانید نگاهی به پایگاه های اطلاعات دانشگاهی بیندازید.
• اگر تحقیق شما، یک تحقیق عمومی است، ممکن است جدولی وجود داشته باشد که بتوانید از آن استفاده کنید.
• از ماشین حساب حجم نمونه استفاده کنید.
یادتان باشد که چون فرمول خاصی وجود ندارد، یعنی اینکه دیگر نمی توانید فرمولی برای انجام کار پیدا کنید. روش های زیادی هستند که می توانید از آنها استفاده کنید و این فقط بستگی به این دارد که آیا چیزی درباره نمونه مورد نظر خود می دانید یا خیر. حتی می توانید استفاده از فرمول های Slovin و یا Cochran هم استفاده کنید.

معایب

در این روش باید ضمن تجزیه و تحلیل متغیرهای جدید، فرضیات خاصی را نیز در نظر بگیرید. این کار می تواند باعث شود که فرض نادرستی به وجود آید. این خاطر در صورتی که ضمن تجزیه و تحلیل آماری رخ دهد، می تواند اثر منفی بر بقیه تحلیل داده شما هم داشته باشد. به این نوع خطاها، خطاهای نمونه گیری گفته می شود که با فاصله اطمینان اندازه گیری می شوند. مثلا معنی اینکه سطح اطمینان نتایج شما ۹۰ درصد است، این است که باید با انجام چند باره تجزیه و تحلیل، بازهم نتایج شما ۹۰ درصد مواقع یکسان باشند.

جمع بندی

در نهایت مهم نیست کدام یک از این روش های تحلیل آماری را استفاده می کنید، فقط مطمئن شوید که حواستان به معایب و نیز فرمول های منحصر به فرد هر کدام هست. البته هیچ استاندارد طلایی و یا روش درست و غلطی وجود ندارد. همه چیز بستگی به داده هایی دارد که جمع آوری کرده اید و بینشی که قرار است در نتیجه نهایی به دست آورید.